打卡信奥刷题（1992）用C++实现信奥 P10714 【MX-X1-T2】「KDOI-05」简单的有限网格问题

P10714 【MX-X1-T2】「KDOI-05」简单的有限网格问题

题目背景

原题链接：https://oier.team/problems/X1B。

题目描述

小 S 在玩一款小游戏。游戏中会有一个 $n\times m$ 的棋盘，其中 $k$ 个位置上有星星。初始有一个捕捉器，在 $(x,y)$ 位置。每次操作，你可以将捕捉器移动到同行或同列的某个位置，使得新位置与原位置不同且必须保证新位置 $(x^{\prime },y^{\prime })$ 满足 $1\le x^{\prime }\le n$，$1\le y^{\prime }\le m$。捕捉器会捕捉 $(x,y)$ 到 $(x^{\prime },y^{\prime })$ 路径上所有的星星。一个星星被捕捉后将会消失。

游戏的目标是在恰好两步内获得尽可能多的星星，然而小 S 不会玩，于是每次就会随意挑选一个可以移动到的新位置进行移动。对于 $(n+m-2{)}^2$ 种小 S 的不同移动方案，求捕捉到的星星数量之和，答案对 $10^9+7$ 取模。

输入格式

第一行三个正整数 $n,m,k$，表示棋盘大小与星星个数。

第二行两个正整数 $x,y$，表示捕捉器初始位置。

接下来 $k$ 行，每行两个正整数，表示每颗星星所在的位置 $(p,q)$。每个位置上可以有多颗星星。

输出格式

一行，一个非负整数，表示对于 $(n+m-2{)}^2$ 种小 S 的不同移动方案，他能捕捉到的星星数量之和，对 $10^9+7$ 取模。

输入输出样例 #1

输入 #1

3 3 4
2 2
1 1
1 2
1 3
3 1

输出 #1

11

输入输出样例 #2

输入 #2

5 8 9
2 7
1 7
2 2
4 7
4 5
4 7
2 8
5 2
1 7
1 7

输出 #2

153

说明/提示

【样例解释 #1】

网格图中，一种合法的移动捕捉器的方案是：

$$(2,2)\to (1,2)\to (1,3)$$

在该方案中，可以捕捉到位置在 $(1,2)$ 和 $(1,3)$ 的各 $1$ 颗星星。

【数据范围】

本题采用捆绑测试。

子任务编号	分值	$n\le$	$m\le$
$1$	$5$	$50$	$50$
$2$	$10$	$1000$	$1000$
$3$	$20$	$10^5$	$10^5$
$4$	$25$	$10^5$	$10^9$
$5$	$25$	$10^9$	$10^9$
$6$	$15$	$10^{18}$	$10^{18}$

对于 $100\%$ 的数据，$1\le k\le 10^5$，$1\le n,m\le 10^{18}$，$1\le x,p\le n$，$1\le y,q\le m$，$(x,y)\ne (p,q)$。

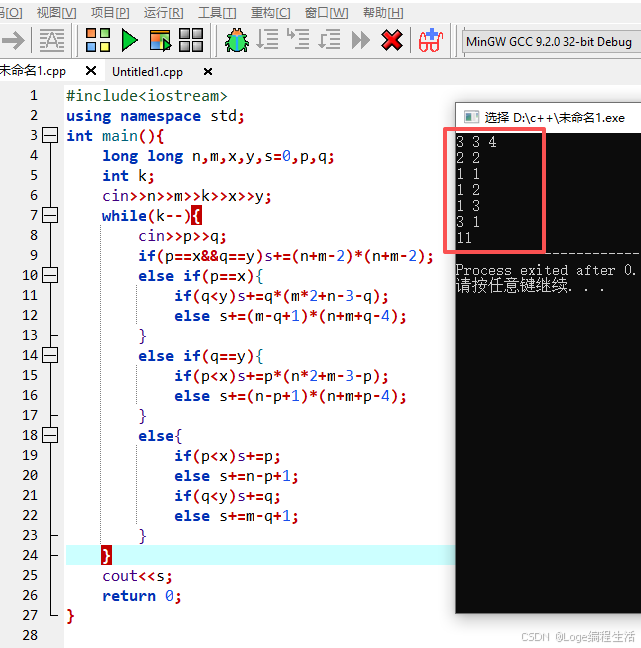
C++实现

#include<iostream>
using namespace std;
int main(){
	long long n,m,x,y,s=0,p,q;
	int k;
	cin>>n>>m>>k>>x>>y;
	while(k--){
		cin>>p>>q;
		if(p==x&&q==y)s+=(n+m-2)*(n+m-2);
		else if(p==x){
			if(q<y)s+=q*(m*2+n-3-q);
			else s+=(m-q+1)*(n+m+q-4);
		}
		else if(q==y){
			if(p<x)s+=p*(n*2+m-3-p);
			else s+=(n-p+1)*(n+m+p-4);
		}
		else{
			if(p<x)s+=p;
			else s+=n-p+1;
			if(q<y)s+=q;
			else s+=m-q+1;
		}
	}
	cout<<s;
	return 0;
}

后续

接下来我会不断用C++来实现信奥比赛中的算法题、GESP考级编程题实现、白名单赛事考题实现，记录日常的编程生活、比赛心得，感兴趣的请关注，我后续将继续分享相关内容