打卡信奥刷题（1584）用C++实现信奥 P6686 混凝土数学

P6686 混凝土数学

题目描述

你正在看混凝土数学，这时旁边的工地开工了，你觉得看他们施工更有意思，于是你向窗外望去，注意到了一些长度不同的木棍。具体而言，你看到了 $n$ 条木棍编号为 $1,2,3,\dots ,n$，长度为 $a_1,a_2,a_3,\dots ,a_n$。你突发奇想：有多少拿出其中 $3$ 条木棍的方案满足它们能构成等腰三角形呢？你不想要输出的数太大，所以最后的方案要对 $998244353$ 取模。

给出等腰三角形的要求：任意两边之和大于第三边且至少有两条边边长相等。

例如，如果木棍长度分别为 {3,3,2,2,4,5}\{3,3,2,2,4,5\}{3,3,2,2,4,5}，你就有 $6$ 种方法，选取的木棍编号分别为：{1,2,3}\{1,2,3\}{1,2,3}，{1,2,4}\{1,2,4\}{1,2,4}，{1,2,5}\{1,2,5\}{1,2,5}，{1,2,6}\{1,2,6\}{1,2,6}，{1,3,4}\{1,3,4\}{1,3,4}，{2,3,4}\{2,3,4\}{2,3,4}。

输入格式

第一行给出一个正整数 $n$ 表示木棍个数。

第二行 $n$ 个正整数表示 $a_1,a_2,a_3,\dots ,a_n$。

输出格式

一个数表示总方案数对 $998244353$ 取模的结果。

输入输出样例 #1

输入 #1

6
3 3 2 2 4 5

输出 #1

6

输入输出样例 #2

输入 #2

6
1 1 4 5 1 4

输出 #2

5

输入输出样例 #3

输入 #3

6
2 2 2 2 2 2

输出 #3

20

说明/提示

• Subtask1 （$30$ pts）：$1\le n\le 200$。
• Subtask2 （$30$ pts）：$1\le n\le 2000$。
• Subtask3 （$20$ pts）：木棍长度全部相等。
• Subtask4 （$20$ pts）：无特殊限制。

对于 $100\%$ 的数据满足：$1\le n\le 2\times 10^5$，$1\le a_i\le 2\times 10^5$。

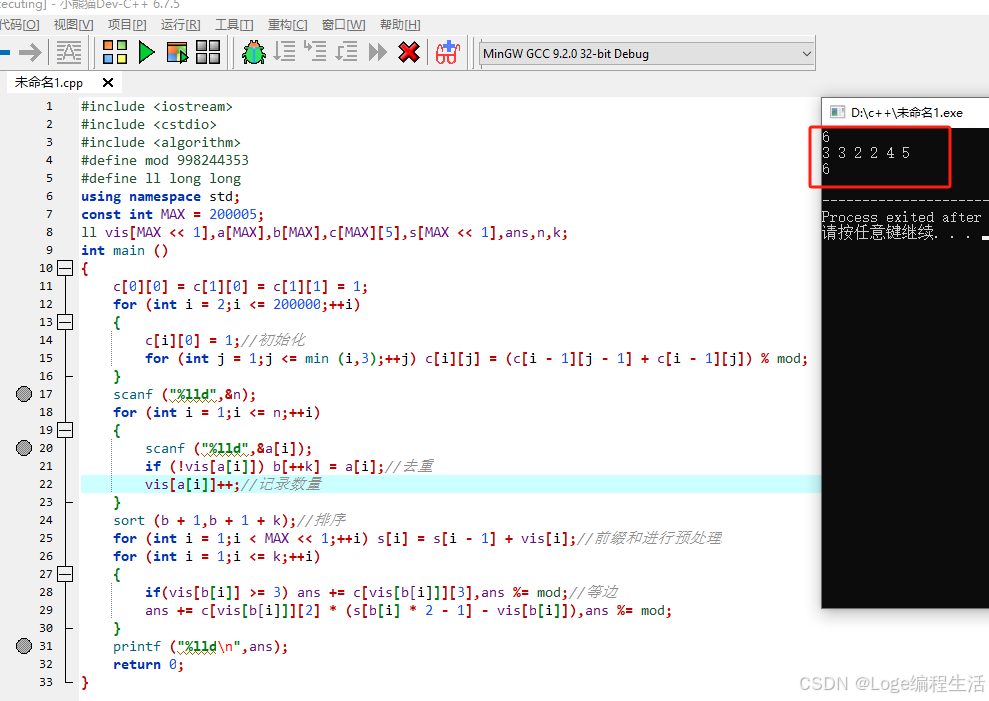
C++实现

#include <iostream>
#include <cstdio>
#include <algorithm>
#define mod 998244353
#define ll long long
using namespace std;
const int MAX = 200005;
ll vis[MAX << 1],a[MAX],b[MAX],c[MAX][5],s[MAX << 1],ans,n,k;
int main ()
{
	c[0][0] = c[1][0] = c[1][1] = 1;
	for (int i = 2;i <= 200000;++i)
	{
		c[i][0] = 1;//初始化
		for (int j = 1;j <= min (i,3);++j) c[i][j] = (c[i - 1][j - 1] + c[i - 1][j]) % mod;	
	}
	scanf ("%lld",&n);
	for (int i = 1;i <= n;++i)
	{
		scanf ("%lld",&a[i]);
		if (!vis[a[i]]) b[++k] = a[i];//去重
		vis[a[i]]++;//记录数量
	} 
	sort (b + 1,b + 1 + k);//排序
	for (int i = 1;i < MAX << 1;++i) s[i] = s[i - 1] + vis[i];//前缀和进行预处理
	for (int i = 1;i <= k;++i)
	{
		if(vis[b[i]] >= 3) ans += c[vis[b[i]]][3],ans %= mod;//等边 
		ans += c[vis[b[i]]][2] * (s[b[i] * 2 - 1] - vis[b[i]]),ans %= mod;
	}
	printf ("%lld\n",ans);
	return 0;
}

后续

接下来我会不断用C++来实现信奥比赛中的算法题、GESP考级编程题实现、白名单赛事考题实现，记录日常的编程生活、比赛心得，感兴趣的请关注，我后续将继续分享相关内容