打卡信奥刷题（1521）用C++实现信奥 P6045 后缀树

P6045 后缀树

题目背景

Eztsu 是一个可爱的女孩子，最近她学习了后缀树，并打算用它来解决如下问题。

题目描述

对于一个字符串 $S$，我们定义 $|S|$ 表示 $S$ 的长度。

接着，我们定义 $S_i$ 表示 $S$ 中第 $i$ 个字符，$S_{L...R}$ 表示由 $S$ 中从左往右数，第 $L$ 个字符到第 $R$ 个字符依次连接形成的字符串。

给定 $n$，求有多少种不同的满足下列要求的串 $S$：

• $|S|=n$。
• $S$ 中仅包含小写字母。
• 不存在整数 $i\in [1,n)$ 使得 $S_{\mathrm{1...}i}$ 是 $S_{i+\mathrm{1...}n}$ 的子串。

对于第三个限制，用通俗一点的说法解释的话，就是不存在一种将这个串分成两段的方式，使得前面一段是后面一段的子串。

两个串 $S$ 和 $T$ 不同当且仅当 $|S|\ne |T|$ 或 $\exists i\in [1,|S|]S_i\ne T_i$。如果你不知道这是什么意思，你可以理解为它们看起来不同。

可怜的 Eztsu 不会做，所以你要帮她做这道题。

答案可能很大，你只需要输出答案对 $998244353$ 取模的值。

题面补充：

$S$ 是 $T$ 的子串当且仅当存在 $L,R\in [1,|T|]$ 使得 $T_{L...R}=S$.

输入格式

一行一个正整数 $n$，意义见题目描述。

输出格式

一行一个整数，答案对 $998244353$ 取模的值。

输入输出样例 #1

输入 #1

2

输出 #1

650

输入输出样例 #2

输入 #2

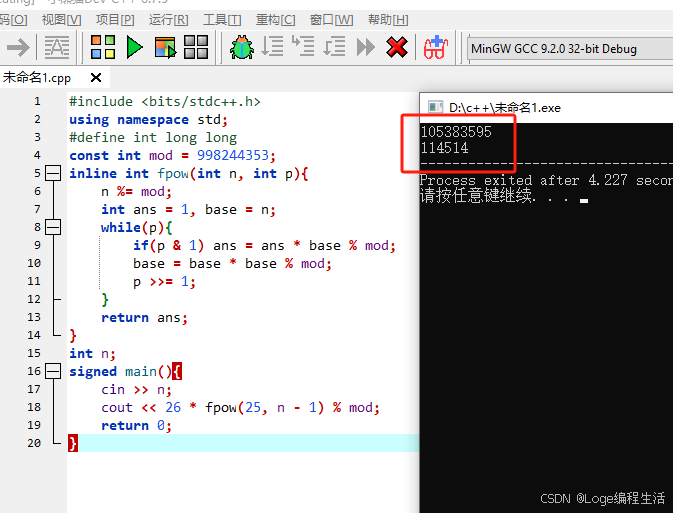
105383595

输出 #2

114514

说明/提示

样例解释

对于第一组样例，不难发现，这个串符合题意当且仅当两个字符不同，因此答案为 $26\times 26-26$，可以理解为两个字符任意的方案数减去两个字符相同的方案数。

---

数据范围

「本题采用捆绑测试」

对于所有测试点，保证 $1\le n\le 10^9$。

$\text{Subtask 1 (17 pts)}$ $n\le 4$。

$\text{Subtask 2 (78 pts)}$ $n\le 2\times 10^3$。

$\text{Subtask 3 (5 pts)}$ 没有特殊限制。

---

提示

小写字母一共有 $26$ 个。

C++实现

#include <bits/stdc++.h>
using namespace std;
#define int long long
const int mod = 998244353;
inline int fpow(int n, int p){
    n %= mod;
    int ans = 1, base = n;
    while(p){
        if(p & 1) ans = ans * base % mod;
        base = base * base % mod;
        p >>= 1;
    }
    return ans;
}
int n;
signed main(){
    cin >> n;
    cout << 26 * fpow(25, n - 1) % mod;
    return 0;
}

后续

接下来我会不断用C++来实现信奥比赛中的算法题、GESP考级编程题实现、白名单赛事考题实现，记录日常的编程生活、比赛心得，感兴趣的请关注，我后续将继续分享相关内容