生成一个均匀的、随机的圆形

转自：https://thecodeway.com/blog/?p=1138

如何生成一个随机的圆形

Posted on 2015年5月24日  by jinchao

        最近在工作中遇到这么一个问题：
        在游戏场景中有一个怪物生成点，这个生长点产生的怪物均匀分布在半径为R的圆形内，这个随机算法应该如何生成？看起来很简单，随手写了一个：

#define   RAND    (( float ) rand () / RAND_MAX )
 
void   get_random_pos ( float   center_x ,  float   center_y ,  float   radius ,  float & x ,  float &  y )
{
     float   u  =  RAND * radius ;
     float   v  =  RAND * 2 * PI ;
    
     x  =  center_x  +  u * cos ( v ) ;
     y  =  center_y  +  u * sin ( v ) ;
}

        但写的过程中，直觉告诉我，这么写肯定是有问题的，试想，如果以北京为例，如果所有居住在北京的人都报出自己家和天安门的距离，那么这些数据肯定不是均匀分布的，因为居住在五环附近的人数肯定要大于居住在二环附近的人数，于是用Mathamatica实验一下：

        果然，这么写是不对的，网上查了一下，这个问题还真是有人研究过，说应该把所获得的随机数开平方一下，实验一下：

        但是，这个开平方背后的数学原理究竟是什么呢？抽空翻了下概率书，原来，其中的道理并不复杂，这里涉及到概率里的一个基本概念，累计分布函数（Cumulative distribution function），简称CFD，它的定义如下：
        设有一个随机变量X，它的取值范围是从负无穷到正无穷，如果把它的值小于x的概率表达为一个函数F(x)，那么这个函数就称为X的累计分布函数

F(x)=P(X≤x)

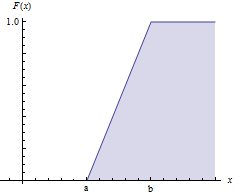
        以最为常见的均匀分布概率为例，设均匀分布的随机变量X的取值范围是[a,b]，那么它的累计分布函数以及函数图像是

F(x)=⎧⎩⎨⎪⎪0x−ab−a1x<aa≤x<bb≤x

        对于一个累计分布函数，符合以下规律

• 0≤F(x)≤1
• F(x)单调递增
• limx→−∞F(x)=0,limx→+∞F(x)=1,

        回到我们的问题中，假设怪物产生的范围的半径为R，随机产生一只怪物时，它和中心的距离是一个随机变量X，显然，对于怪物均匀分布的情况，X落在半径为x的圆内的概率，等于半径为x小圆和半径为X的大圆的面积之比

        也就是说

F(x)=P(X≤x)=x2/R2

        现在我们手头上只有均匀概率的随机数产生器，要想产生这么个随机数需要用到一个很巧妙的运算，就是反函数。设随机变量 u是一个均匀分布在[0,1]之间的随机数，另一个随机变量 X=F−1(u),现在我们需要证明 X的累计分布函数是 F(x)
        证明如下

P(X≤x)=P(F−1(u)≤x)=P(u≤F(x))=F(x)

        初看起来有点复杂，其实在下面的图上可以很直观的理解这个过程：


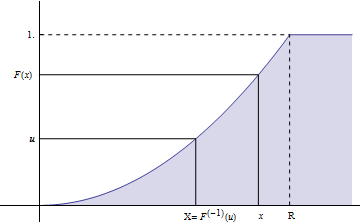
        这是利用了 F(x)是单调递增函数的特性，在我们的问题中， F(x)的反函数可以表达为

F−1(u)=Ru−−√

        所以最终的算法可以写成

#define   RAND    (( float ) rand () / RAND_MAX )
 
void   get_random_pos ( float   center_x ,  float   center_y ,  float   radius ,  float & x ,  float &  y )
{
     float   u  =  sqrt ( RAND ) * radius ;
     float   v  =  RAND * 2 * PI ;
    
     x  =  center_x  +  u * cos ( v ) ;
     y  =  center_y  +  u * sin ( v ) ;
}

Tagged 数学, 程序, 算法