完全背包概述:
完全包解析:和01,包相似只是,每一个物品有任意多个,我们还是借鉴01背包的方法
状态表示:
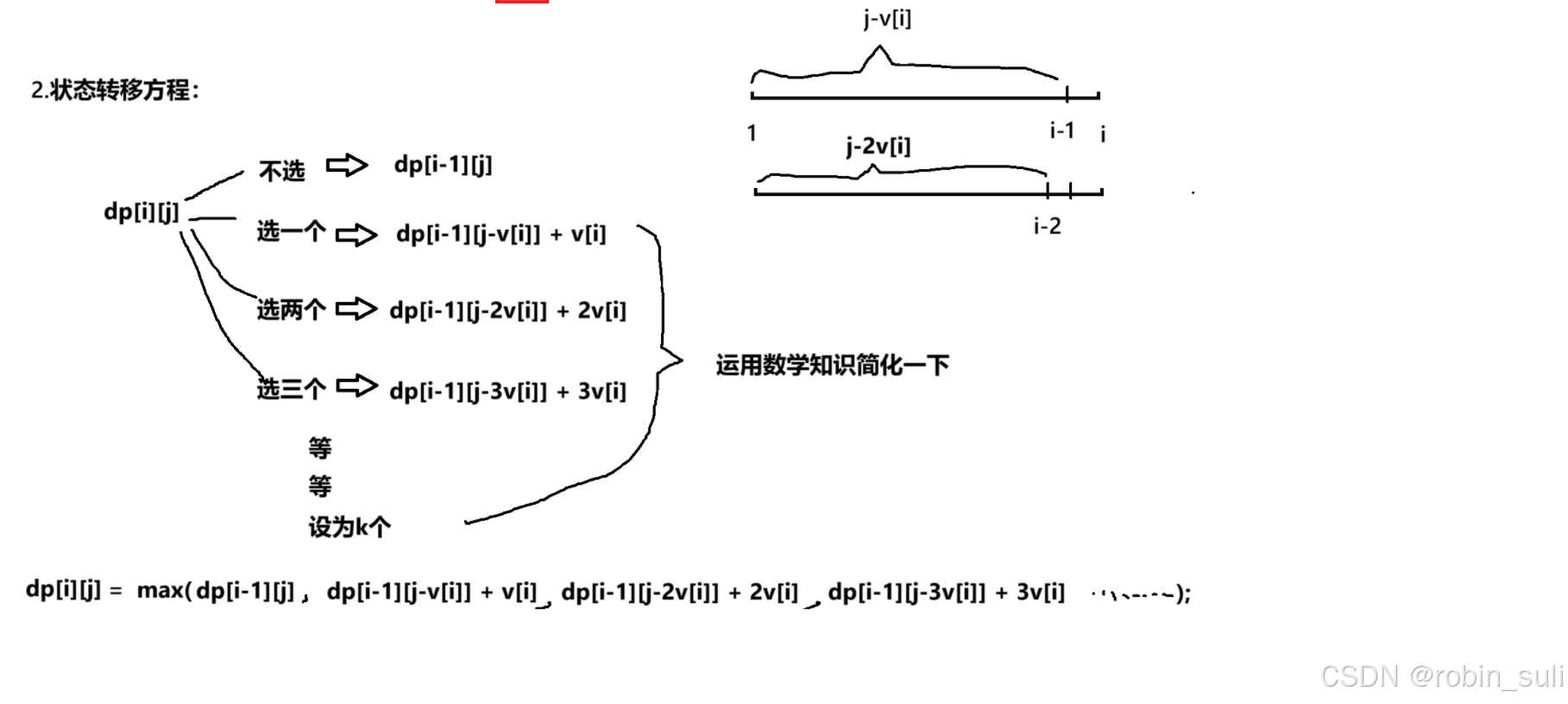
状态转移方程:
初始化:
填表顺序:
返回值:
代码呈现:
import java.util.Scanner;
// 注意类名必须为 Main, 不要有任何 package xxx 信息
public class Main {
public static void main(String[] args) {
Scanner in = new Scanner(System.in);
int n = in.nextInt();
int V = in.nextInt();
int[] v = new int[n+1];
int[] w = new int[n+1];
//构造题目的输入
for(int i = 1; i <= n; i++){
v[i] = in.nextInt();
w[i] = in.nextInt();
}
int[][] dp1 = new int[n+1][V+1];
int[][] dp2 = new int[n+1][V+1];
//第一小问:
for(int i = 1; i <= n; i++)
for(int j = 0; j <= V; j++){
dp1[i][j] = dp1[i-1][j];
if(j >= v[i]){
dp1[i][j] = Math.max(dp1[i][j],dp1[i][j-v[i]] + w[i]);
}
}
System.out.println(dp1[n][V]);
//第二小问:
//初始化:
for(int i = 1; i <= V; i++) dp2[0][i] = -1;
for(int i = 1; i <= n; i++)
for(int j = 0; j <= V; j++){
dp2[i][j] = dp2[i-1][j];
if(j >= v[i] && dp2[i][j-v[i]] != -1){
dp2[i][j] = Math.max(dp2[i][j],dp2[i][j-v[i]] + w[i]);
}
}
System.out.println(dp2[n][V] == -1? 0 : dp2[n][V]);
}
}
利用滚动数组优化:
完全背包,更新的时候由于j-v[i]在同一行,想要正确的“三角”(不被覆盖的数据)更新,就要从左往右去填表
所以完全背包和01背包,反着,不需要修改遍历顺序
不清楚01背包优化的:链接: 点击
优化代码呈现:
import java.util.Scanner;
// 注意类名必须为 Main, 不要有任何 package xxx 信息
public class Main {
//优化版本:
public static void main(String[] args) {
Scanner in = new Scanner(System.in);
int n = in.nextInt();
int V = in.nextInt();
int[] v = new int[n+1];
int[] w = new int[n+1];
//构造题目的输入
for(int i = 1; i <= n; i++){
v[i] = in.nextInt();
w[i] = in.nextInt();
}
int[] dp1 = new int[V+1];
int[] dp2 = new int[V+1];
//第一小问:
for(int i = 1; i <= n; i++)
for(int j = v[i]; j <= V; j++){
dp1[j] = Math.max(dp1[j],dp1[j-v[i]] + w[i]);
}
System.out.println(dp1[V]);
//第二小问:
//初始化:
for(int i = 1; i <= V; i++) dp2[i] = -1;
for(int i = 1; i <= n; i++)
for(int j = v[i]; j <= V; j++){
if(dp2[j-v[i]] != -1)
dp2[j] = Math.max(dp2[j],dp2[j-v[i]] + w[i]);
}
System.out.println(dp2[V] == -1? 0 : dp2[V]);
}
}



























 5万+
5万+

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?










