目录
1. SARSA(State-Action-Reward-State-Action)
嗨,欢迎来到强化学习的世界!🎉
在强化学习中,时序差分学习(Temporal Difference Learning,简称TD) 是一种非常核心且优雅的学习方法。它巧妙地结合了蒙特卡洛方法(Monte Carlo) 和动态规划(Dynamic Programming) 的优点,是现代强化学习算法的基石。
今天我们就来深入了解TD学习的原理、公式推导以及经典算法!💪
为什么需要TD学习?
在介绍TD之前,我们先回顾一下其他两种方法的特点:
| 方法 | 优点 | 缺点 |
|---|---|---|
| 动态规划(DP) | 利用贝尔曼方程进行自举(Bootstrap) | 需要完整的环境模型 |
| 蒙特卡洛(MC) | 不需要环境模型,从经验中学习 | 必须等到回合结束才能更新 |
TD学习的出现就是为了取两者之长:
-
像MC一样,不需要环境模型
-
像DP一样,可以在线更新(不用等回合结束)
TD学习的核心思想
1. 价值函数的定义
首先,回顾状态价值函数的定义:

其中:
-
是策略
-
是折扣因子
-
是在时刻
获得的奖励
2. TD(0) 更新公式
TD学习的核心更新公式如下:
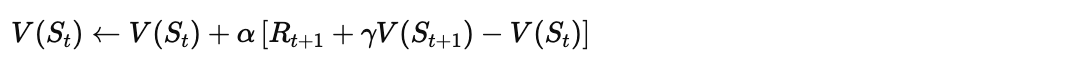
让我们拆解这个公式:
| 符号 | 含义 |
|---|---|
| 学习率(步长),控制更新幅度 | |
| 执行动作后获得的即时奖励 | |
| 下一状态的折扣价值估计 | |
| TD目标(TD Target) | |
| TD误差(TD Error),记作 |
3. TD误差的直观理解

TD误差可以理解为"惊喜程度":
-
:实际情况比预期好 😊
-
:实际情况比预期差 😢
-
:与预期一致 😐
TD学习流程图
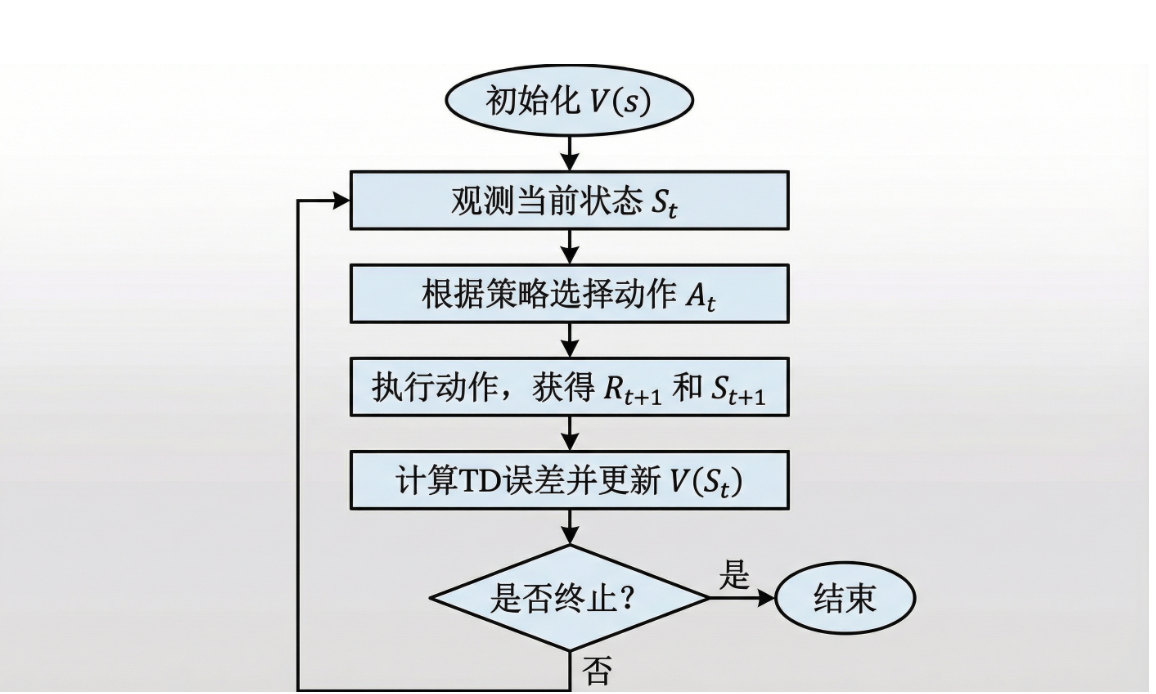
经典TD算法:SARSA与Q-Learning
1. SARSA(State-Action-Reward-State-Action)
SARSA是一种同策略(On-policy) TD控制算法,直接学习动作价值函数 。
更新公式:
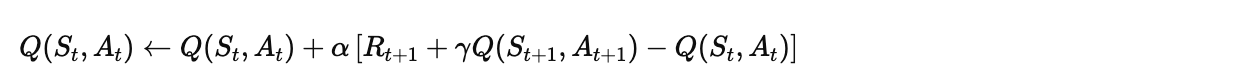
算法伪代码:
初始化 Q(s, a) 为任意值
对于每个回合:
初始化状态 S
根据Q选择动作 A(如ε-greedy)
重复(对于回合中的每一步):
执行动作 A,观测 R, S'
根据Q选择动作 A'(如ε-greedy)
Q(S, A) ← Q(S, A) + α[R + γQ(S', A') - Q(S, A)]
S ← S'
A ← A'
直到 S 是终止状态
2. Q-Learning
Q-Learning是一种异策略(Off-policy) TD控制算法。
更新公式:
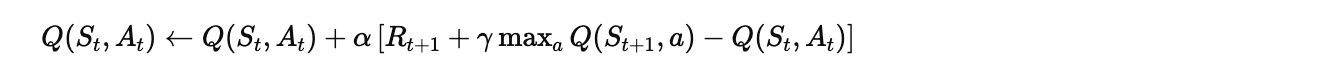
关键区别: Q-Learning使用 而不是实际采取的动作的Q值。
算法伪代码:
初始化 Q(s, a) 为任意值
对于每个回合:
初始化状态 S
重复(对于回合中的每一步):
根据Q选择动作 A(如ε-greedy)
执行动作 A,观测 R, S'
Q(S, A) ← Q(S, A) + α[R + γ max_a Q(S', a) - Q(S, A)]
S ← S'
直到 S 是终止状态
3. SARSA vs Q-Learning 对比
【请在此处插入对比示意图】
📝 图示说明:请绘制一个"悬崖行走"(Cliff Walking)环境示意图,包含:
-
网格世界:4行×12列的网格
-
起点S:左下角,用绿色标注
-
终点G:右下角,用蓝色标注
-
悬崖区域:底部一行中间的10个格子,用红色/阴影标注,表示危险区域
-
两条路径:
-
路径1(安全路径):用虚线箭头标注,沿着网格上方绕行,标注"SARSA倾向选择"
-
路径2(最优路径):用实线箭头标注,紧贴悬崖边缘走,标注"Q-Learning倾向选择"
-
-
图例:说明两种算法的不同行为特点
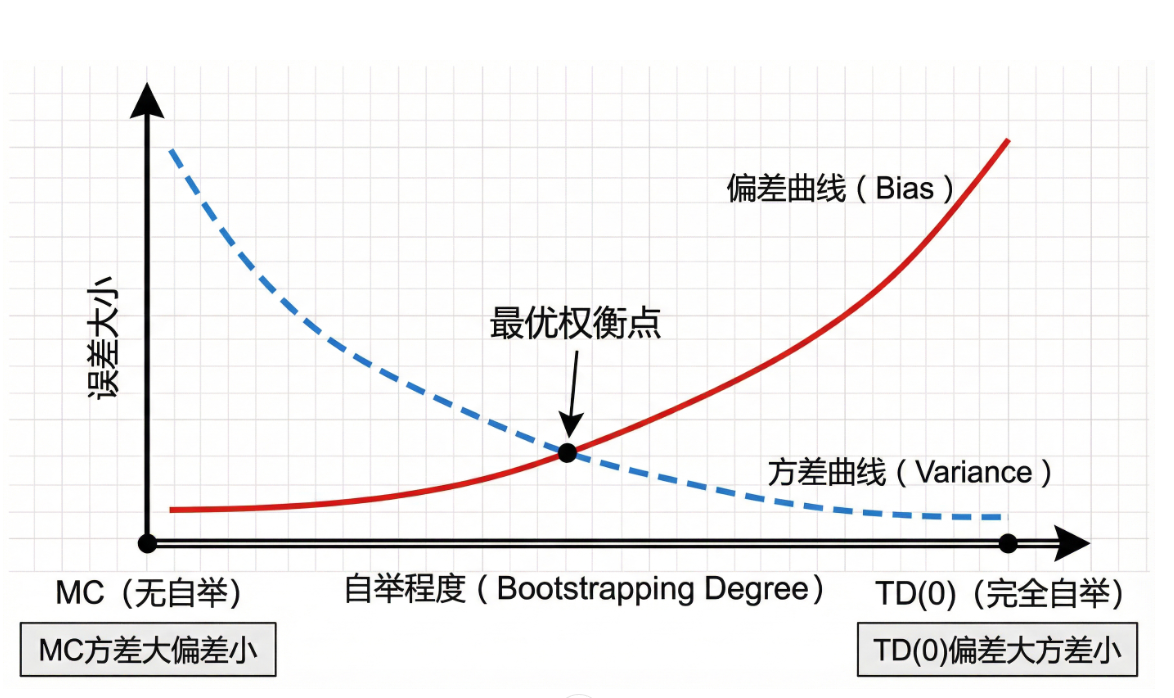
TD与MC方法的偏差-方差权衡
【请在此处插入偏差-方差权衡示意图】
拓展:TD(λ) 与资格迹
1. n步TD方法
TD(0)只看一步,而我们可以扩展到n步:

更新公式变为:

| n值 | 方法类型 |
|---|---|
| n = 1 | TD(0) |
| n = ∞ | 蒙特卡洛 |
| 1 < n < ∞ | n步TD |
2. TD(λ) 算法
TD(λ)巧妙地结合了所有n步回报的加权平均:

其中 是衰减参数:
-
等价于 TD(0)
-
等价于 MC
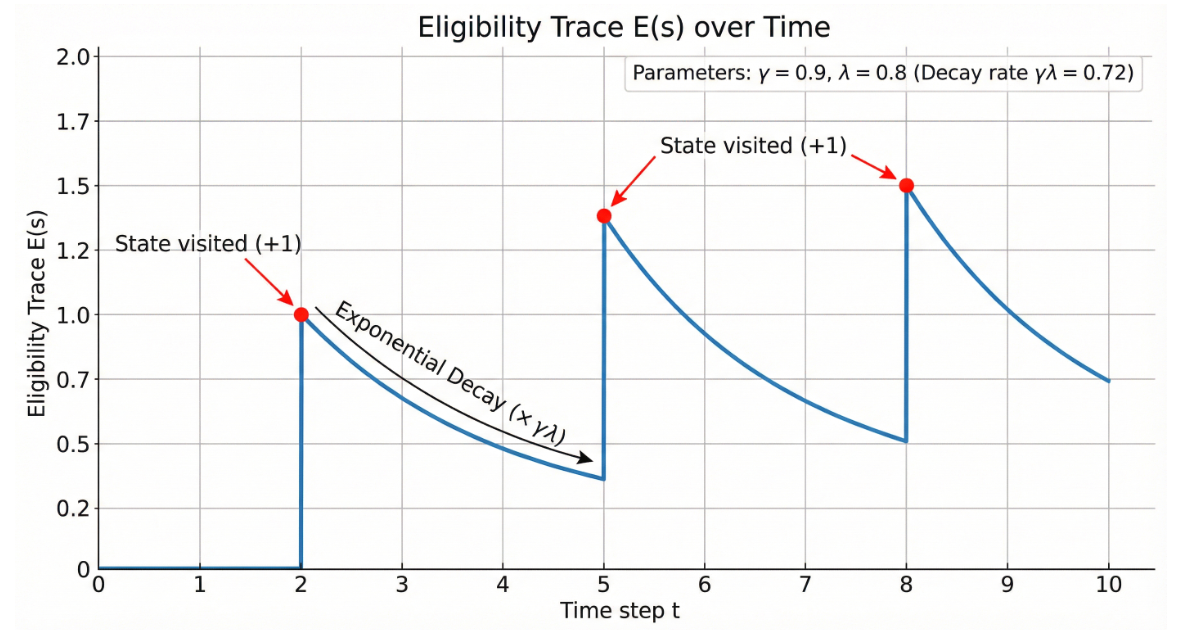
3. 资格迹(Eligibility Traces)
资格迹是一种高效实现TD(λ)的技术:

更新规则:

实践小贴士
-
学习率选择:
通常取0.01~0.1,太大会震荡,太小收敛慢
-
探索策略:常用ε-greedy,ε一般从1.0逐渐衰减到0.01
-
初始化:乐观初始化可以促进探索
-
回放缓冲区:结合经验回放可以提高样本效率
总结
| 特性 | 动态规划 | 蒙特卡洛 | TD学习 |
|---|---|---|---|
| 需要环境模型 | ✅ 是 | ❌ 否 | ❌ 否 |
| 需要完整回合 | ❌ 否 | ✅ 是 | ❌ 否 |
| 自举 | ✅ 是 | ❌ 否 | ✅ 是 |
| 在线学习 | ✅ 是 | ❌ 否 | ✅ 是 |
TD学习是强化学习中的核心方法,理解它对于学习更高级的算法(如DQN、Actor-Critic等)至关重要!
希望这篇文章对你有帮助!如果有任何问题,欢迎在评论区讨论 💬
觉得不错的话,别忘了点赞收藏哦! ⭐👍






















 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








