目录
1. 什么是动态规划?
1.1 动态规划的本质
动态规划(Dynamic Programming,简称DP)是一种通过把复杂问题分解成子问题来求解的方法。
🌟 核心思想:大问题的最优解可以由小问题的最优解推导出来!
在强化学习中,动态规划用于在已知环境模型的情况下,计算最优策略。
1.2 使用DP的两个前提条件
| 条件 | 说明 |
|---|---|
| 最优子结构 | 问题的最优解包含子问题的最优解 |
| 重叠子问题 | 子问题会被反复计算,可以存储避免重复 |
1.3 DP在强化学习中的定位
┌─────────────────────────────────────────────────────────┐
│ 强化学习方法分类 │
├─────────────────────────────────────────────────────────┤
│ ┌──────────────┐ ┌──────────────┐ ┌──────────────┐ │
│ │ 动态规划 │ │ 蒙特卡洛 │ │ 时序差分 │ │
│ │ (DP) │ │ (MC) │ │ (TD) │ │
│ ├──────────────┤ ├──────────────┤ ├──────────────┤ │
│ │ ✅ 需要模型 │ │ ❌ 不需模型 │ │ ❌ 不需模型 │ │
│ │ ✅ 自举 │ │ ❌ 不自举 │ │ ✅ 自举 │ │
│ │ 完整备份 │ │ 采样备份 │ │ 采样备份 │ │
│ └──────────────┘ └──────────────┘ └──────────────┘ │
└─────────────────────────────────────────────────────────┘
重要提示:DP是基于模型(Model-Based) 的方法,需要完整知道环境的状态转移概率和奖励函数!
2. 前置知识回顾
在深入DP之前,让我们快速回顾几个关键概念~
2.1 马尔可夫决策过程(MDP)
MDP由五元组定义:
| 符号 | 含义 | 说明 |
|---|---|---|
| 状态空间 | 所有可能状态的集合 | |
| 动作空间 | 所有可能动作的集合 | |
| 状态转移概率 | P(s' | s, a) = 在状态s执行动作a转移到s'的概率 | |
| 奖励函数 | R(s, a, s') = 获得的即时奖励 | |
| 折扣因子 |
2.2 策略(Policy)
策略 定义了智能体的行为方式:

-
确定性策略:每个状态对应唯一动作,
-
随机性策略:每个状态对应动作的概率分布,
2.3 价值函数
状态价值函数 
从状态 开始,遵循策略
,期望获得的累积回报:

动作价值函数 
从状态 开始,先执行动作
,然后遵循策略
,期望获得的累积回报:
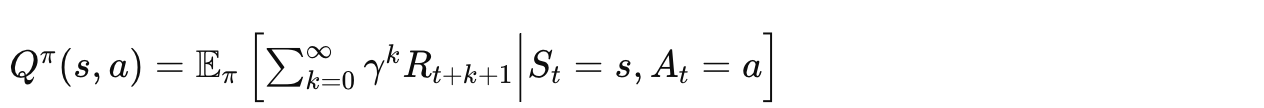
两者的关系

3. 贝尔曼方程详解
贝尔曼方程是动态规划的灵魂!它建立了当前状态价值和后继状态价值之间的递归关系。
3.1 贝尔曼期望方程
状态价值的贝尔曼期望方程
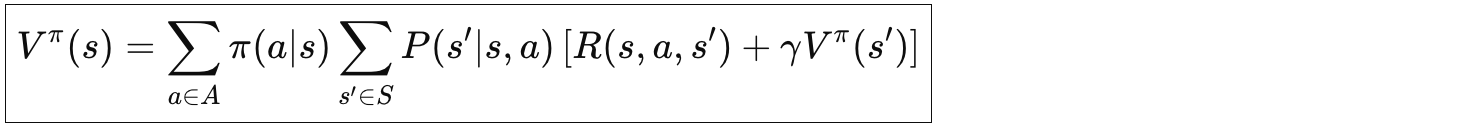
让我们逐步拆解这个公式:
当前状态价值 V(s) =
∑ [选择动作a的概率] ×
∑ [转移到s'的概率] ×
[即时奖励 + 折扣 × 下一状态价值]
直观理解:
┌─────┐
│ s │ ← 当前状态
└──┬──┘
│ π(a|s) 按策略选择动作
▼
┌─────┐
│ a │ ← 执行动作
└──┬──┘
│ P(s'|s,a) 环境响应
▼
┌─────┴─────┐
▼ ▼
┌─────┐ ┌─────┐
│ s'₁ │ │ s'₂ │ ← 可能的下一状态
└─────┘ └─────┘
R₁ R₂ ← 对应的奖励
动作价值的贝尔曼期望方程
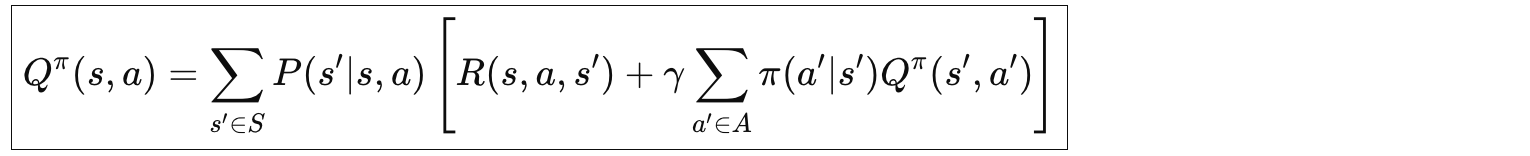
3.2 贝尔曼最优方程
当我们追求最优策略时,需要用到贝尔曼最优方程:
最优状态价值函数
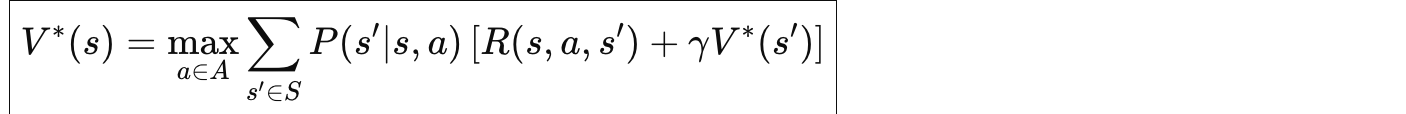
最优动作价值函数
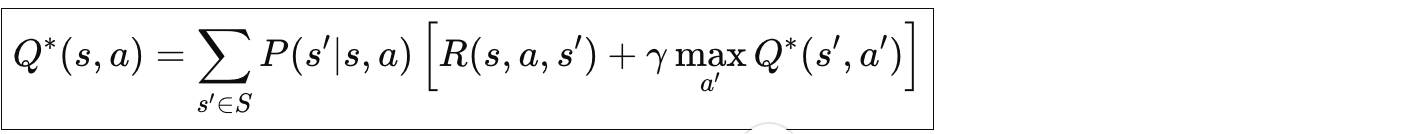
💡 核心区别
| 方程类型 | 关键操作 | 含义 |
|---|---|---|
| 贝尔曼期望方程 | 按策略概率加权 | |
| 贝尔曼最优方程 | 选择最优动作 |
3.3 贝尔曼方程的矩阵形式
对于策略评估,我们可以把贝尔曼期望方程写成矩阵形式:

其中:
-
是状态价值向量
-
是期望即时奖励向量
-
是状态转移概率矩阵
理论上可以直接求解:

但当状态空间很大时,矩阵求逆计算量太大 ,所以我们需要迭代方法! 🔄
4. 策略评估(Policy Evaluation)
4.1 什么是策略评估?
🎯 目标:给定一个策略
,计算该策略下所有状态的价值函数
这是一个预测问题:我们不改变策略,只是评估它有多好。
4.2 迭代策略评估算法
通过反复应用贝尔曼期望方程进行迭代:
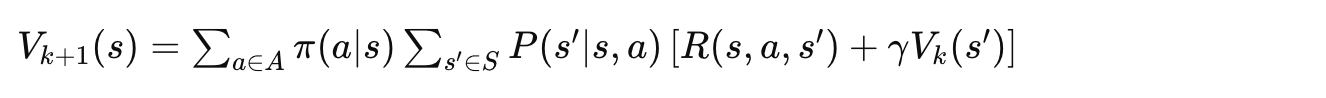
4.3 算法流程
┌─────────────────────────────────────────────────────────┐
│ 迭代策略评估算法 │
├─────────────────────────────────────────────────────────┤
│ 输入:策略 π,精度阈值 θ │
│ 输出:价值函数 V ≈ V^π │
├─────────────────────────────────────────────────────────┤
│ 1. 初始化 V(s) = 0,对所有 s ∈ S │
│ 2. repeat: │
│ Δ ← 0 │
│ for 每个状态 s ∈ S: │
│ v ← V(s) │
│ V(s) ← Σ_a π(a|s) Σ_s' P(s'|s,a)[R + γV(s')] │
│ Δ ← max(Δ, |v - V(s)|) │
│ until Δ < θ │
│ 3. 返回 V │
└─────────────────────────────────────────────────────────┘
4.4 收敛性证明(直观理解)
为什么迭代策略评估一定会收敛?🤔
关键:这是一个压缩映射(Contraction Mapping)!
定义贝尔曼算子:
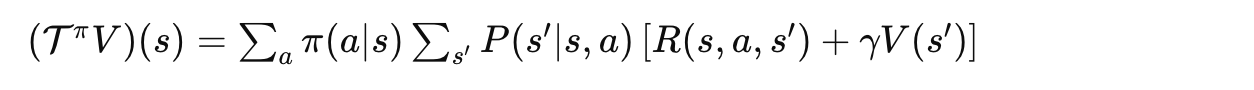
可以证明:

由于,每次迭代都在"压缩"误差,最终必然收敛到唯一的不动点
4.5 小例子:简单网格世界
考虑一个 2×2 的网格世界:
┌───┬───┐
│ 1 │ 2 │
├───┼───┤
│ 3 │ 4 │
└───┴───┘
-
状态4是终点,奖励为0
-
其他转移奖励为-1
-
采用均匀随机策略(每个方向概率0.25)
-
迭代过程:
| 迭代 | V(1) | V(2) | V(3) | V(4) |
|---|---|---|---|---|
| k=0 | 0 | 0 | 0 | 0 |
| k=1 | -1 | -1 | -1 | 0 |
| k=2 | -2 | -1.5 | -1.5 | 0 |
| k=3 | -2.5 | -2 | -2 | 0 |
| ... | ... | ... | ... | ... |
| k=∞ | -3 | -2 | -2 | 0 |
5. 策略改进(Policy Improvement)
5.1 什么是策略改进?
目标:根据当前价值函数,找到一个更好(或至少一样好)的策略
5.2 策略改进定理
定理:对于策略 和
,如果对所有状态
都有:

那么策略 不劣于
,即:

5.3 贪婪策略改进
基于当前价值函数,采用贪婪策略:
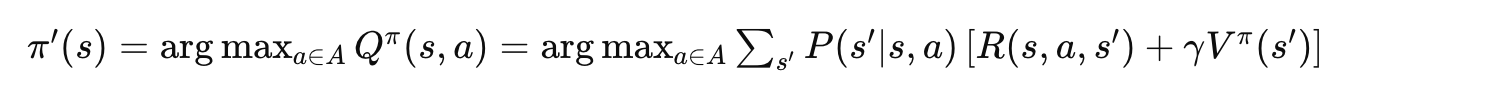
5.4 图示理解
策略改进过程:
V^π(s) V^π'(s)
│ │
┌───────┼───────┐ ┌───────┼───────┐
│ │ │ │ │ │
▼ ▼ ▼ 改进 ▼ ▼ ▼
Q(s,a₁) Q(s,a₂) Q(s,a₃) ───→ 选择 max Q(s,a)
│ │ │ │
└───────┴───────┘ │
│ │
选择最大的Q值对应的动作 新策略在s处选择该动作
5.5 为什么贪婪改进有效?
直观理解:
-
当前策略
在状态
选择动作
-
新策略
在状态
选择
-
由于选择了Q值最大的动作,至少不会变差!
-
如果存在更好的动作,就会变得更好!
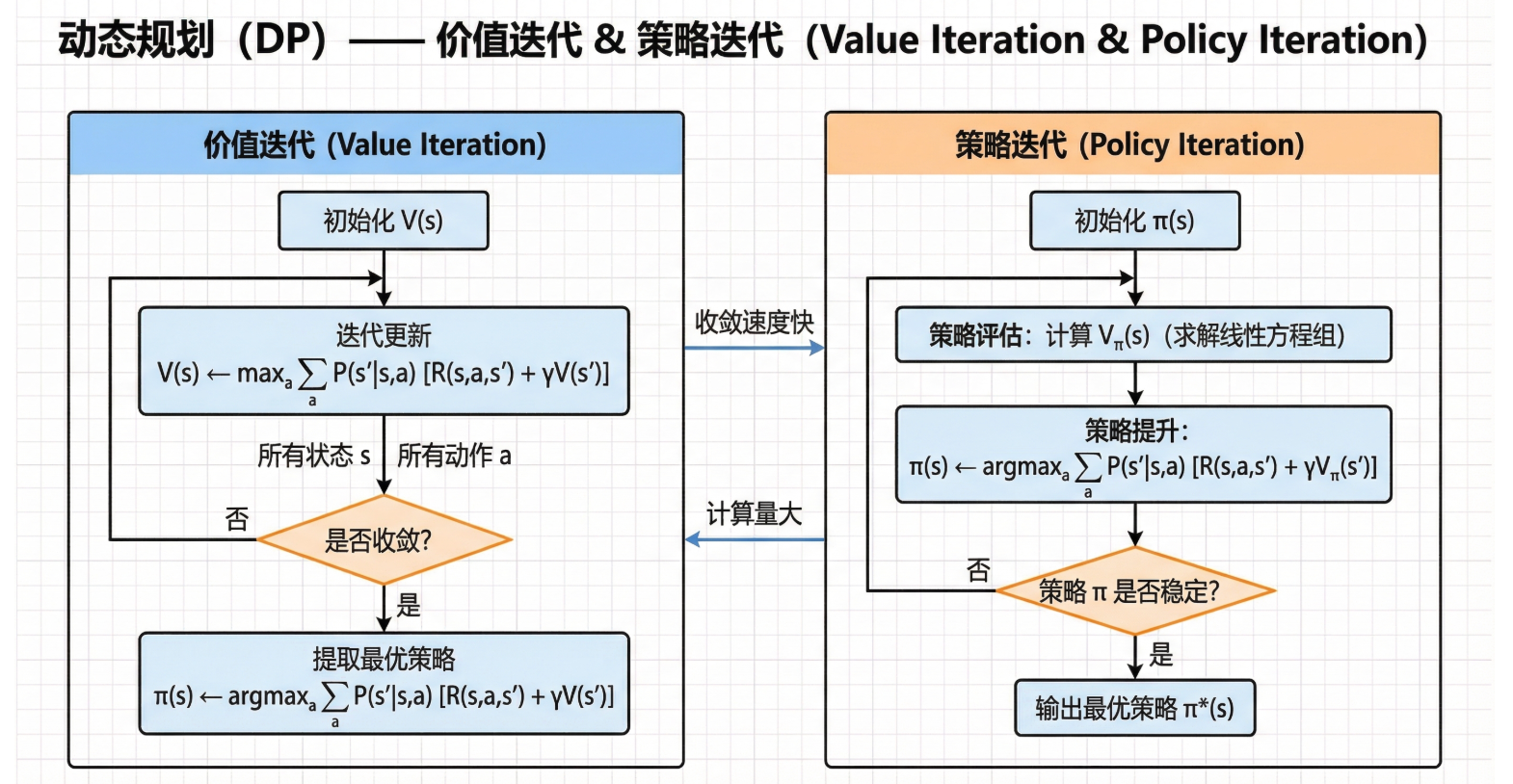
6. 策略迭代(Policy Iteration)
6.1 核心思想
策略迭代把策略评估和策略改进结合起来,交替进行:

6.2 算法流程
┌─────────────────────────────────────────────────────────────────┐
│ 策略迭代算法 │
├─────────────────────────────────────────────────────────────────┤
│ 输入:MDP <S, A, P, R, γ> │
│ 输出:最优策略 π* 和最优价值函数 V* │
├─────────────────────────────────────────────────────────────────┤
│ 1. 初始化: │
│ 随机初始化策略 π(s),对所有 s ∈ S │
│ 初始化 V(s) = 0,对所有 s ∈ S │
│ │
│ 2. 策略评估(循环直到收敛): │
│ repeat: │
│ Δ ← 0 │
│ for 每个状态 s ∈ S: │
│ v ← V(s) │
│ V(s) ← Σ_s' P(s'|s,π(s))[R(s,π(s),s') + γV(s')] │
│ Δ ← max(Δ, |v - V(s)|) │
│ until Δ < θ │
│ │
│ 3. 策略改进: │
│ policy_stable ← true │
│ for 每个状态 s ∈ S: │
│ old_action ← π(s) │
│ π(s) ← argmax_a Σ_s' P(s'|s,a)[R(s,a,s') + γV(s')] │
│ if old_action ≠ π(s): │
│ policy_stable ← false │
│ │
│ 4. 如果 policy_stable = true,停止并返回 π 和 V │
│ 否则,返回步骤2 │
└─────────────────────────────────────────────────────────────────┘
6.3 流程图
┌─────────────┐
│ 开始 │
└──────┬──────┘
│
▼
┌─────────────┐
│ 初始化策略π │
└──────┬──────┘
│
▼
┌──────────────────────┐
│ │
│ ┌────────────────┐ │
│ │ 策略评估 │ │
│ │ 计算 V^π │ │
│ └───────┬────────┘ │
│ │ │
│ ▼ │
│ ┌────────────────┐ │
│ │ 策略改进 │ │
│ │ π ← greedy(V) │ │
│ └───────┬────────┘ │
│ │ │
└──────────┼───────────┘
│
▼
┌─────────────┐
│ 策略稳定? │
└──────┬──────┘
│
┌──────┴──────┐
│ Yes │ No
▼ └────────────┐
┌─────────────┐ │
│ 输出π*, V* │ │
└─────────────┘ │
│
┌──────────────────────────┘
│
└───────────────────→ 返回策略评估
6.4 收敛性分析
为什么策略迭代一定会收敛?
-
有限策略数:对于有限状态和动作空间,策略数量是有限的(最多 $|A|^{|S|}$ 种)
-
单调改进:每次策略改进要么提升策略,要么保持不变
-
必然收敛:由于策略数有限且单调不降,必然在有限步内收敛到最优
7. 价值迭代(Value Iteration)
7.1 核心思想
价值迭代的关键洞察:我们不需要等策略评估完全收敛! 🎯
实际上,我们可以在每次迭代中同时进行价值更新和策略改进:
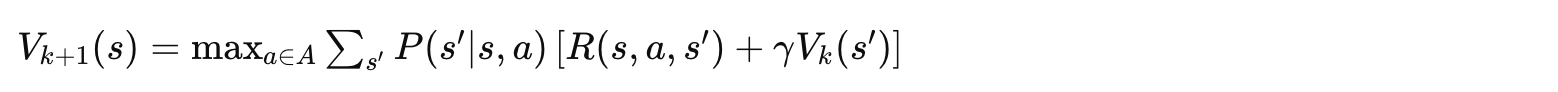
这正是贝尔曼最优方程的迭代应用!
7.2 与策略迭代的关系
价值迭代可以看作是策略迭代的一种极端情况:
-
策略迭代:完整策略评估 + 策略改进
-
价值迭代:单步策略评估 + 策略改进(合二为一)
策略迭代: 评估 → 评估 → ... → 评估 → 改进 → 评估 → ...
↑__________________________|
价值迭代: (评估+改进) → (评估+改进) → (评估+改进) → ...
7.3 算法流程
┌─────────────────────────────────────────────────────────────────┐
│ 价值迭代算法 │
├─────────────────────────────────────────────────────────────────┤
│ 输入:MDP <S, A, P, R, γ>,精度阈值 θ │
│ 输出:最优策略 π* 和最优价值函数 V* │
├─────────────────────────────────────────────────────────────────┤
│ 1. 初始化: │
│ V(s) = 0,对所有 s ∈ S(终止状态价值为0) │
│ │
│ 2. 价值更新(循环直到收敛): │
│ repeat: │
│ Δ ← 0 │
│ for 每个状态 s ∈ S: │
│ v ← V(s) │
│ V(s) ← max_a Σ_s' P(s'|s,a)[R(s,a,s') + γV(s')] │
│ Δ ← max(Δ, |v - V(s)|) │
│ until Δ < θ │
│ │
│ 3. 提取最优策略: │
│ for 每个状态 s ∈ S: │
│ π*(s) ← argmax_a Σ_s' P(s'|s,a)[R(s,a,s') + γV(s')] │
│ │
│ 4. 返回 π* 和 V* │
└─────────────────────────────────────────────────────────────────┘
7.4 流程图
┌─────────────┐
│ 开始 │
└──────┬──────┘
│
▼
┌─────────────┐
│ 初始化 V(s) │
│ = 0 │
└──────┬──────┘
│
▼
┌──────────────────────┐
│ for 每个状态 s: │
│ │
│ V(s) ← max_a [...] │◄────────┐
│ │ │
└──────────┬───────────┘ │
│ │
▼ │
┌─────────────┐ │
│ 收敛了吗? │ │
└──────┬──────┘ │
│ │
┌──────┴──────┐ │
│ No │ Yes │
└─────────────┴─────────────┘
│
▼
┌─────────────────┐
│ 提取最优策略 │
│ π*(s) = argmax │
└────────┬────────┘
│
▼
┌─────────────────┐
│ 输出 π*, V* │
└─────────────────┘
7.5 收敛性保证
价值迭代的贝尔曼最优算子 也是压缩映射:
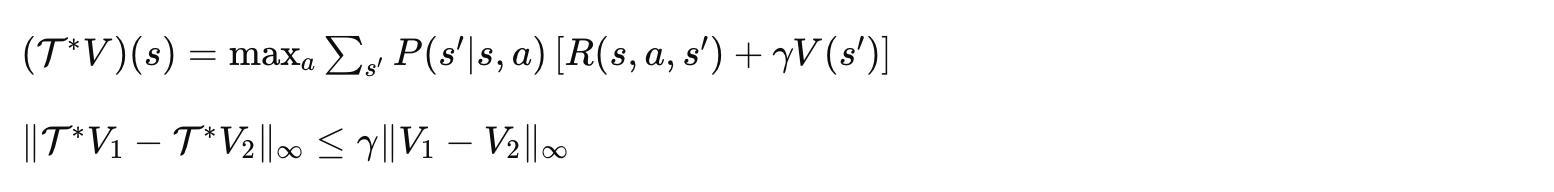
因此必然收敛到唯一的最优价值函数!
7.6 收敛速度
误差界:经过 次迭代后:

这告诉我们:
-
越小,收敛越快
-
需要
次迭代达到
精度
8. 策略迭代 vs 价值迭代
8.1 详细对比
| 特性 | 策略迭代 | 价值迭代 |
|---|---|---|
| 核心操作 | 完整策略评估 + 策略改进 | 单步最优更新 |
| 每次迭代复杂度 | 较高(需要内循环收敛) | 较低(只需一次遍历) |
| 迭代次数 | 较少 | 较多 |
| 总体效率 | 状态空间小时更优 | 状态空间大时更优 |
| 存储需求 | 需要存储策略 | 只需存储价值 |
| 实现复杂度 | 稍复杂 | 简单 |
8.2 时间复杂度深入分析
策略迭代
-
策略评估:
每次迭代 × 需要多次迭代收敛
-
策略改进:
-
外循环:通常很少(对于大多数问题 < 10次)
价值迭代
-
每次迭代:
-
收敛需要:
次迭代
8.3 选择建议
选择决策树
│
▼
┌─────────────────────┐
│ 状态空间规模? │
└──────────┬──────────┘
│
┌─────────────┼─────────────┐
│ │ │
▼ ▼ ▼
小规模 中规模 大规模
(< 100) (100-10000) (> 10000)
│ │ │
▼ ▼ ▼
┌─────────┐ ┌──────────┐ ┌──────────┐
│策略迭代 │ │ 都可以 │ │价值迭代 │
│或价值迭代│ │ 测试决定 │ │或近似方法│
└─────────┘ └──────────┘ └──────────┘
8.4 折中方案:广义策略迭代(GPI)
实际应用中,我们常常使用介于两者之间的方法:
-
策略评估不需要完全收敛
-
可以进行
步评估后就改进策略(
)
-
灵活调整评估深度以优化性能
9. 代码实战:网格世界
让我们用一个经典的网格世界例子来实践!
9.1 问题设定
┌─────┬─────┬─────┬─────┐
│ 0 │ 1 │ 2 │ 3 │
├─────┼─────┼─────┼─────┤
│ 4 │ 5 │ 6 │ 7 │
├─────┼─────┼─────┼─────┤
│ 8 │ 9 │ 10 │ 11 │
├─────┼─────┼─────┼─────┤
│ 12 │ 13 │ 14 │ 15 │
└─────┴─────┴─────┴─────┘
- 状态0和状态15是终点
- 每走一步奖励为-1
- 动作:上、下、左、右(撞墙原地不动)
- γ = 1.0
9.2 Python代码实现
import numpy as np
class GridWorld:
"""4x4网格世界环境"""
def __init__(self):
self.size = 4
self.n_states = 16
self.n_actions = 4 # 上、下、左、右
self.terminal_states = [0, 15]
self.gamma = 1.0
# 动作映射:上(0)、下(1)、左(2)、右(3)
self.actions = {
0: (-1, 0), # 上
1: (1, 0), # 下
2: (0, -1), # 左
3: (0, 1) # 右
}
def state_to_pos(self, state):
"""状态编号转坐标"""
return state // self.size, state % self.size
def pos_to_state(self, row, col):
"""坐标转状态编号"""
return row * self.size + col
def get_next_state(self, state, action):
"""获取下一状态和奖励"""
if state in self.terminal_states:
return state, 0
row, col = self.state_to_pos(state)
d_row, d_col = self.actions[action]
new_row = max(0, min(self.size - 1, row + d_row))
new_col = max(0, min(self.size - 1, col + d_col))
next_state = self.pos_to_state(new_row, new_col)
reward = -1
return next_state, reward
def policy_evaluation(env, policy, theta=1e-6):
"""
策略评估
参数:
env: 环境
policy: 策略矩阵 [n_states, n_actions],表示每个状态下选择各动作的概率
theta: 收敛阈值
返回:
V: 价值函数数组
"""
V = np.zeros(env.n_states)
iteration = 0
while True:
delta = 0
for s in range(env.n_states):
if s in env.terminal_states:
continue
v = V[s]
new_v = 0
for a in range(env.n_actions):
next_s, reward = env.get_next_state(s, a)
# 确定性环境,转移概率为1
new_v += policy[s, a] * (reward + env.gamma * V[next_s])
V[s] = new_v
delta = max(delta, abs(v - V[s]))
iteration += 1
if delta < theta:
break
print(f"策略评估收敛,迭代次数: {iteration}")
return V
def policy_improvement(env, V):
"""
策略改进
参数:
env: 环境
V: 当前价值函数
返回:
new_policy: 改进后的策略
policy_stable: 策略是否稳定
"""
new_policy = np.zeros((env.n_states, env.n_actions))
policy_stable = True
for s in range(env.n_states):
if s in env.terminal_states:
new_policy[s] = 1.0 / env.n_actions # 终止状态均匀分布
continue
# 计算每个动作的Q值
q_values = np.zeros(env.n_actions)
for a in range(env.n_actions):
next_s, reward = env.get_next_state(s, a)
q_values[a] = reward + env.gamma * V[next_s]
# 贪婪选择(可能有多个最优动作)
best_actions = np.argwhere(q_values == np.max(q_values)).flatten()
new_policy[s, best_actions] = 1.0 / len(best_actions)
return new_policy
def policy_iteration(env, theta=1e-6):
"""
策略迭代算法
参数:
env: 环境
theta: 收敛阈值
返回:
policy: 最优策略
V: 最优价值函数
"""
# 初始化随机策略
policy = np.ones((env.n_states, env.n_actions)) / env.n_actions
iteration = 0
while True:
iteration += 1
print(f"\n=== 策略迭代第 {iteration} 轮 ===")
# 策略评估
V = policy_evaluation(env, policy, theta)
# 策略改进
new_policy = policy_improvement(env, V)
# 检查策略是否改变
if np.allclose(policy, new_policy):
print("策略已收敛!")
break
policy = new_policy
print(f"\n策略迭代总轮数: {iteration}")
return policy, V
def value_iteration(env, theta=1e-6):
"""
价值迭代算法
参数:
env: 环境
theta: 收敛阈值
返回:
policy: 最优策略
V: 最优价值函数
"""
V = np.zeros(env.n_states)
iteration = 0
while True:
delta = 0
for s in range(env.n_states):
if s in env.terminal_states:
continue
v = V[s]
# 计算所有动作的Q值并取最大
q_values = []
for a in range(env.n_actions):
next_s, reward = env.get_next_state(s, a)
q_values.append(reward + env.gamma * V[next_s])
V[s] = max(q_values)
delta = max(delta, abs(v - V[s]))
iteration += 1
if delta < theta:
break
print(f"价值迭代收敛,迭代次数: {iteration}")
# 提取最优策略
policy = np.zeros((env.n_states, env.n_actions))
for s in range(env.n_states):
if s in env.terminal_states:
policy[s] = 1.0 / env.n_actions
continue
q_values = np.zeros(env.n_actions)
for a in range(env.n_actions):
next_s, reward = env.get_next_state(s, a)
q_values[a] = reward + env.gamma * V[next_s]
best_actions = np.argwhere(q_values == np.max(q_values)).flatten()
policy[s, best_actions] = 1.0 / len(best_actions)
return policy, V
def print_value_function(V, size=4):
"""打印价值函数"""
print("\n价值函数:")
print("-" * 40)
for i in range(size):
row = V[i*size:(i+1)*size]
print(" | ".join([f"{v:7.2f}" for v in row]))
print("-" * 40)
def print_policy(policy, size=4):
"""打印策略"""
action_symbols = ['↑', '↓', '←', '→']
print("\n最优策略:")
print("-" * 40)
for i in range(size):
row_str = []
for j in range(size):
s = i * size + j
if s in [0, 15]:
row_str.append(" * ")
else:
# 找出概率最大的动作
best_actions = np.argwhere(policy[s] == np.max(policy[s])).flatten()
symbols = ''.join([action_symbols[a] for a in best_actions])
row_str.append(f"{symbols:^5}")
print(" | ".join(row_str))
print("-" * 40)
# 运行示例
if __name__ == "__main__":
env = GridWorld()
print("=" * 50)
print(" 策略迭代算法")
print("=" * 50)
policy_pi, V_pi = policy_iteration(env)
print_value_function(V_pi)
print_policy(policy_pi)
print("\n" + "=" * 50)
print(" 价值迭代算法")
print("=" * 50)
policy_vi, V_vi = value_iteration(env)
print_value_function(V_vi)
print_policy(policy_vi)
# 验证两种方法结果一致
print("\n两种方法价值函数差异:", np.max(np.abs(V_pi - V_vi)))
9.3 运行结果
==================================================
策略迭代算法
==================================================
=== 策略迭代第 1 轮 ===
策略评估收敛,迭代次数: 174
=== 策略迭代第 2 轮 ===
策略评估收敛,迭代次数: 4
=== 策略迭代第 3 轮 ===
策略评估收敛,迭代次数: 1
策略已收敛!
策略迭代总轮数: 3
价值函数:
----------------------------------------
0.00 | -1.00 | -2.00 | -3.00
-1.00 | -2.00 | -3.00 | -2.00
-2.00 | -3.00 | -2.00 | -1.00
-3.00 | -2.00 | -1.00 | 0.00
----------------------------------------
最优策略:
----------------------------------------
* | ← | ← | ↓←
↑ | ↑← | ↓← | ↓
↑ | ↑→ | ↓→ | ↓
↑→ | → | → | *
----------------------------------------
==================================================
价值迭代算法
==================================================
价值迭代收敛,迭代次数: 7
价值函数:
----------------------------------------
0.00 | -1.00 | -2.00 | -3.00
-1.00 | -2.00 | -3.00 | -2.00
-2.00 | -3.00 | -2.00 | -1.00
-3.00 | -2.00 | -1.00 | 0.00
----------------------------------------
最优策略:
----------------------------------------
* | ← | ← | ↓←
↑ | ↑← | ↓← | ↓
↑ | ↑→ | ↓→ | ↓
↑→ | → | → | *
----------------------------------------
两种方法价值函数差异: 0.0
10. 总结与思考
10.1 本文要点回顾
| 主题 | 关键点 |
|---|---|
| 动态规划基础 | 需要完整环境模型,基于贝尔曼方程迭代求解 |
| 贝尔曼方程 | 建立当前价值和未来价值的递归关系 |
| 策略评估 | 给定策略,迭代计算价值函数 |
| 策略改进 | 基于价值函数,贪婪地改进策略 |
| 策略迭代 | 交替进行评估和改进,策略层面收敛 |
| 价值迭代 | 直接迭代贝尔曼最优方程,价值层面收敛 |
10.2 核心公式汇总
┌─────────────────────────────────────────────────────────────┐
│ 核心公式速查表 │
├─────────────────────────────────────────────────────────────┤
│ 贝尔曼期望方程(状态价值): │
│ V^π(s) = Σ_a π(a|s) Σ_s' P(s'|s,a)[R + γV^π(s')] │
│ │
│ 贝尔曼最优方程(状态价值): │
│ V*(s) = max_a Σ_s' P(s'|s,a)[R + γV*(s')] │
│ │
│ 策略评估更新: │
│ V_{k+1}(s) = Σ_a π(a|s) Σ_s' P(s'|s,a)[R + γV_k(s')] │
│ │
│ 价值迭代更新: │
│ V_{k+1}(s) = max_a Σ_s' P(s'|s,a)[R + γV_k(s')] │
│ │
│ 贪婪策略改进: │
│ π'(s) = argmax_a Σ_s' P(s'|s,a)[R + γV(s')] │
└─────────────────────────────────────────────────────────────┘
10.3 DP方法的局限性
虽然DP方法很强大,但也有其局限性:
| 局限性 | 说明 |
|---|---|
| 需要完整模型 | 必须知道转移概率P和奖励函数R |
| 维度灾难 | 状态空间大时计算量爆炸 |
| 无法处理连续空间 | 需要离散化或函数近似 |
10.4 下一步学习
掌握了DP之后,可以继续学习:
动态规划 (Model-Based)
│
├──→ 蒙特卡洛方法 (Model-Free, 完整轨迹)
│
└──→ 时序差分方法 (Model-Free, 单步更新)
│
├──→ SARSA (On-Policy)
│
└──→ Q-Learning (Off-Policy)
课后思考题
-
思考题1:如果折扣因子 $\gamma = 0$,价值迭代会发生什么?
-
思考题2:在策略迭代中,如果我们只进行一次策略评估的迭代就进行策略改进,这与价值迭代有什么关系?
-
实践题:修改代码,在网格世界中加入一个"陷阱"状态(奖励为-10),观察最优策略的变化。
🎉 恭喜你完成了动态规划的学习!
这是强化学习中非常重要的基础,虽然内容较多,但每一个概念都是构建后续知识的基石。如果有任何疑问,欢迎在评论区讨论!💬
如果这篇文章对你有帮助,别忘了点赞👍、收藏⭐、关注🔔 三连哦!





















 2077
2077










