逻辑回归代码实现

理论

• Logistic回归：用于预测结果是界于0和1之间的概率
• 在Logistic回归中，对数几率是关于X是线性变化的。
• 几率（odds）：该事件发生的概率与该事件不发生的概率的比值
• 0-1事件中事件1发生的概率为P，0发生的概率就是1-P;
• 事件1发生的几率：

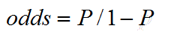
• 对数几率：
  
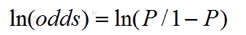
• 根据概率公式：
  
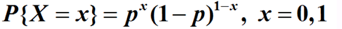
• 通过对数几率：
  
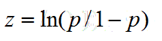
  推导出:
  
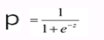
  根据线性关系:
  
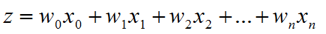
  W为回归系数;
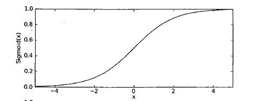
  这个函数对应的sigmoid函数为:
  
  
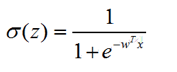
  这里的w怎么求？？(可以对比线性回归里面的w是利用梯度下降法求解的)
  利用极大似然估算( 方便利用梯度上升的方法)
  这里简单讲一下何为极大似然估算:
  
  

概率函数：

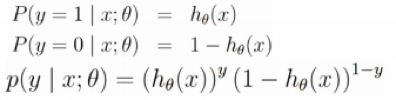
对数似然:

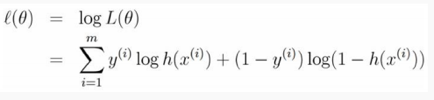
梯度:

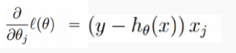
梯度上升的伪代码:

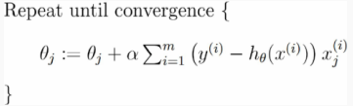
其中：θ 表示回归系数(这里的θ指的是下面中的weights), α 表示步长

代码

import numpy as np
# import  pysnooper

# @pysnooper.snoop()
def loadDataSet():
    dataMat = []