基于可达性矩阵的电网分区及孤岛辨识

针对含有DG的配电网，当受到攻击发生解列，进行孤岛检测将是对保持电网的稳定运行将是非常有必要的。
下面就简单介绍一下利用可达性矩阵对电网进行分区以及进行孤岛辨识。
可达性矩阵的定义及计算步骤如下：
定义：可达矩阵，指的是用矩阵形式来描述有向连接图各节点之间经过一定长度的通路后可达到的程度。
计算步骤：

对于可达性矩阵的电网分和孤岛辨识具体过程如下：
首先配电网的拓扑结构如下图所示：

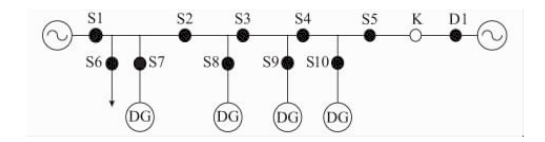
由上图可得到配电网的邻接矩阵:

针对上述邻接矩阵，进行幂乘运算，得到矩阵的各次幂，并对各次幂矩阵进行位或运算，则可得到配电网的可达性矩阵。上述计算得到的可达性矩阵如下：

上述矩阵中，1代表对应节点通过若干条支路进行连通，即在（i,j）=1，表示从起点i出发，经过若干条支路后可到达中点j，节点i和节点j具有连通性。

可达性矩阵中，相同的行或列则属于同一个分区。到此，完成了基于可达性矩阵的分区。

孤岛辨识：则需要先构建一个开关向量K，用来表述配电网各个节点的具体属性。此例中的开关向量为K = [1 0 0 0 0 -1 -2 -2 -2 -2],其中1表示节点与电源相连接，处于并网状态；0表示节点属于联络节点；-1表示节点为负荷节点；-2表示对应