五种基本的排序算法（JavaScript版）

排序算法一直都是笔试和面试的一个必考点，这次我们就通过实例的讲解，给出JavaScript版本的排序算法。
我们先初始化一个算法的构造函数，然后将各种排序算法都作为方法写在构造函数的内部，构造函数如下所示：

		function ArrayList() {
            var array = [];
            this.insert = function (item) {
                array.push(item);
            };

            this.toString = function () {
                return array.join();
            };
            // 交换变量的值
            function swap(index1, index2){
                var flag = array[index1];
                array[index1] = array[index2];
                array[index2] = flag;

            };
		}
		//构建数组实例
		function CreateSortArray(num) {
            var array = new ArrayList();
            for(var i = num; i > 0; i--){
                array.insert(i);
            }

            return array;
        }

冒泡排序 — 时间复杂度O(n^2)

冒泡双循环，外层循环控制需要确立元素回到正确位置的次数，最后一个元素自动回到正确的位置上面；内层循环将相邻的元素两两进行比较，如果第一个比第二个大，就交换他们，直至结束。因为数组后面的元素已经是有序的，所以内层循环次数必须减去排序好元素的大小。
代码如下：

this.bubbleSort = function () {
    for(var i = 0; i < array.length; i++)
        for(var j = 0; j < array.length - 1 - i; j++) 
                    {
                        if(array[j] > array[j + 1])
                        {
                            swap(j, j + 1);
                        }
                    }
            };

选择排序 – 时间复杂度O(n^2)

算法思想： 首先我们假定第一个元素为最小的元素，在后面的元素中找出最小的，与第一个进行位置交换，若第一个本身都是最小的，我们则不变位置，以此类推，得到数组的升序排列。
代码如下：

			this.selectionSort = function () {
                var length = array.length;
                for(var i = 0; i < length - 1; i++){
                    indexMin = i;
                    for(var j = i + 1; j < length; j++)
                    {
                        if(array[i] > array[j])
                        {
                            indexMin = j;
                        }
                    }
                    if(i !== indexMin)
                    {
                        swap(i, indexMin);
                    }
                }
            };

插入排序 — 时间复杂度O(n^2)

算法思想：假定第一个元素是已经排过序的，后面的元素与前面的元素进行比较，比自身大的就交换位置，小的则位置不变。
代码如下：

			this.insertionSort = function () {
                var temp;
                for(var i = 1; i < array.length; i++)
                {
                    j = i;
                    temp = array[i];
                    while(j > 0 && array[j] < array[j - 1])
                    {
                        array[j] = array[j - 1];
                        j--;
                    }
                    array[j] = temp;
                }

                return array;
            };

归并排序 — 时间复杂度O(nlog * n)

算法思想：使用递归将一个大的数组分成n(n代表数组的长度)个只有一个元素的列表，然后再使用合并算法进行合并，相当于数组拆分，再给元素进行排序合并，效果图如下：

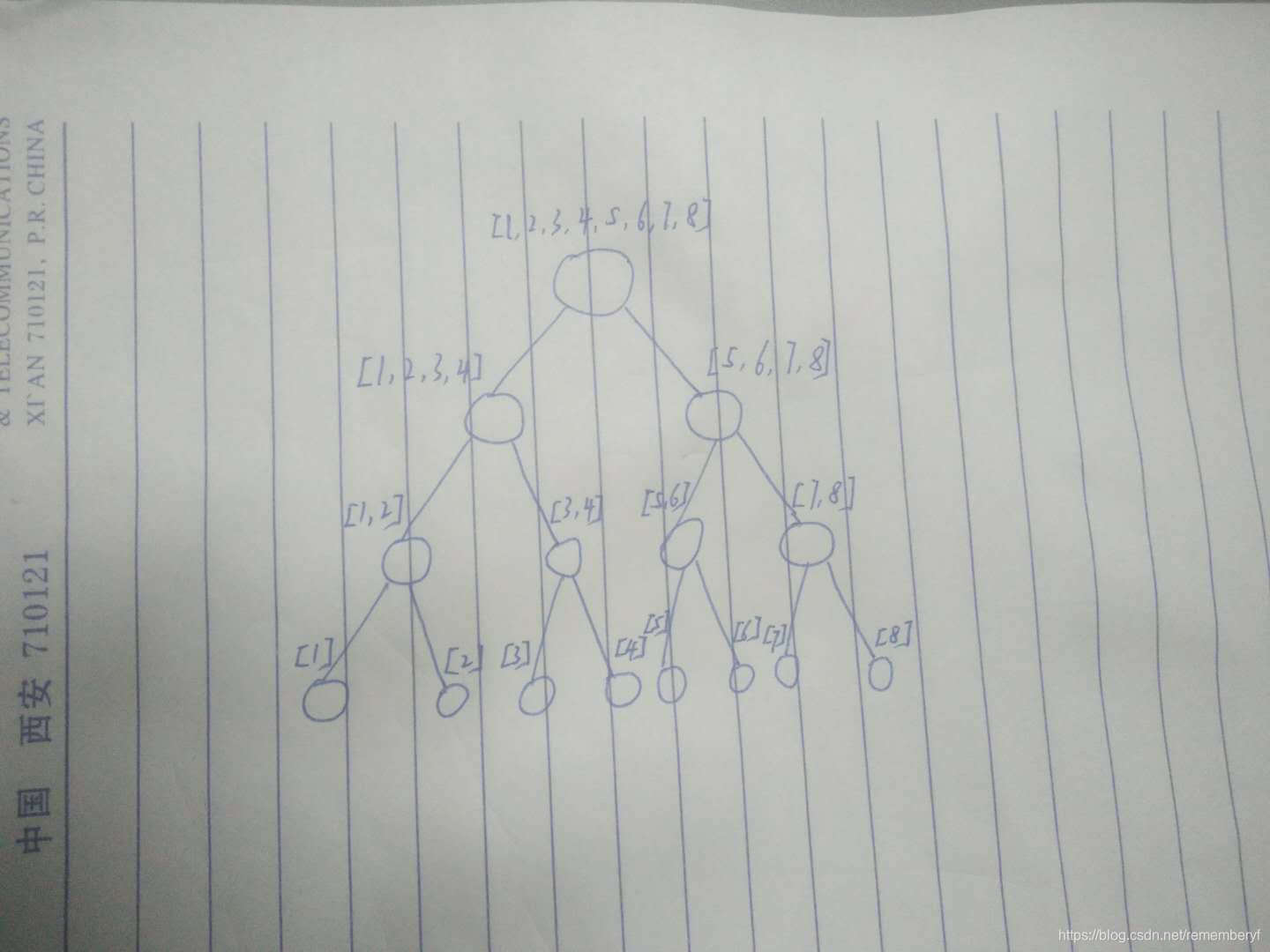
在理解了思想后，我们来看看代码：

		this.mergeSort = function () {
                array = mergeSortRec(array);
            };

            var mergeSortRec = function (array) {
                var length = array.length;
                if(length === 1)
                {
                    return array;
                }
                var mid = Math.floor(length / 2);
                var left = array.slice(0, mid);
                var right = array.slice(mid, length);

                return merge(mergeSortRec(left), mergeSortRec(right));
            };

            var merge = function (left, right) {
                var result = [];
                var il = 0, ir = 0;
                while(il < left.length && ir < right.length)
                {
                    if(left[il] < right[ir])
                    {
                        result.push(left[il++]);
                    }else{
                        result.push(right[ir++]);
                    }
                }

                while(il < left.length)
                {
                    result.push(left[il++]);
                }

                while(ir < right.length)
                {
                    result.push(right[ir++]);
                }

                return result;
            };

快速排序 — 时间复杂度O(nlog^n)

算法思想：我们先从数组的中间确定一个元素为主元，将其划分为无限小的序列，然后从数组的头部确立头指针，尾部确立尾指针。依次与主元进行比较，左边比主元大的，右边比主元小的，将依次交互位置，重复 以上操作，实现快速升序排列，快速排序的性能比其它同复杂度的要好。
代码如下：

		this.quickSort = function() {
                quick(array, 0, array.length - 1);
            };
            var quick = function (array, left, right){
                var index;
                if(array.length > 1){
                    index = partition(array, left, right);
                    if(left < index - 1){
                        quick(array, left, index - 1);
                    }
                    if(index < right){
                        quick(array, index, right);
                    }
                }
            };

            var partition = function (array, left, right) {
                var provt = array[Math.floor((left + right) / 2)];
                var i = left,
                    j = right;

                while(i <= j) {
                    while(array[i] < provt) {
                        i++;
                    }
                    while(array[j] > provt) {
                        j--;
                    }

                    if(i <= j) {
                        swapQuickSort(array, i, j);
                        i++;
                        j--;
                    }
                }

                return i;
            };

            var swapQuickSort = function (array, index1, index2) {
                var flag = array[index1];
                array[index1] = array[index2];
                array[index2] = flag;
            };

二分搜索法

算法思想： 在数组中寻找一个特定的值，我们可以从数组的中间将其分隔开，当然前提是数组是已经排序过的，同中间值进行比较，然后重复之前的操作，直至找出来要比较的值。
代码如下：

			this.binarySearch = function (item) {
                this.quickSort();    //使用快排进行排序
                var low = 0,
                    high = array.length - 1,
                    mid,
                    element;

                while(low <= high){
                    mid = Math.floor((low + high) /2);
                    element = array[mid];

                    if(item < element) {
                        high = mid - 1;
                    }else if(item > element){
                        low = mid + 1;
                    }else{
                        return mid;
                    }
                }

                return -1;
            };

代码测试

		var array = new CreateSortArray(5);
        console.log(array.toString());
        array.bubbleSort();
        console.log(array.toString());
        array.selectionSort();
        console.log(array.toString());
        array.insertionSort();
        console.log(array.toString());
        array.mergeSort();
        console.log(array.toString());
        array.quickSort();
        console.log(array.toString());
        console.log(array.binarySearch(1));

效果图如下所示：

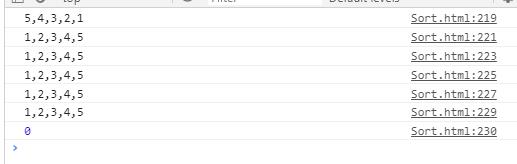
源码：git源码地址
以上就是对算法的一些复习，如果有什么不足，望大家指出来，一起进步。