贪心第一天，别太贪了

今天是贪心第一天，做376. 摆动序列时脑子都要干烧了，贪心的题还是很有意思的，对于理论知识，我觉得做题的时候就想这两个问题吧：

如何找到局部最优解呢？用这个局部最优解模拟示例后能通过吗？

455.分发饼干

假设你是一位很棒的家长，想要给你的孩子们一些小饼干。但是，每个孩子最多只能给一块饼干。

对每个孩子 i，都有一个胃口值 g[i]，这是能让孩子们满足胃口的饼干的最小尺寸；并且每块饼干 j，都有一个尺寸 s[j] 。如果 s[j] >= g[i]，我们可以将这个饼干 j 分配给孩子 i ，这个孩子会得到满足。你的目标是尽可能满足越多数量的孩子，并输出这个最大数值。

示例 1:

输入: g = [1,2,3], s = [1,1]
输出: 1
解释:
你有三个孩子和两块小饼干，3个孩子的胃口值分别是：1,2,3。
虽然你有两块小饼干，由于他们的尺寸都是1，你只能让胃口值是1的孩子满足。
所以你应该输出1。
示例 2:

输入: g = [1,2], s = [1,2,3]
输出: 2
解释:
你有两个孩子和三块小饼干，2个孩子的胃口值分别是1,2。
你拥有的饼干数量和尺寸都足以让所有孩子满足。
所以你应该输出2.

这道题有一个坑挺有意思的，我自己做的时候直接用双指针遍历，没想过这个坑，就是代码随想录里的这段：

“不能 先遍历 饼干，再遍历胃口”

原因如图：

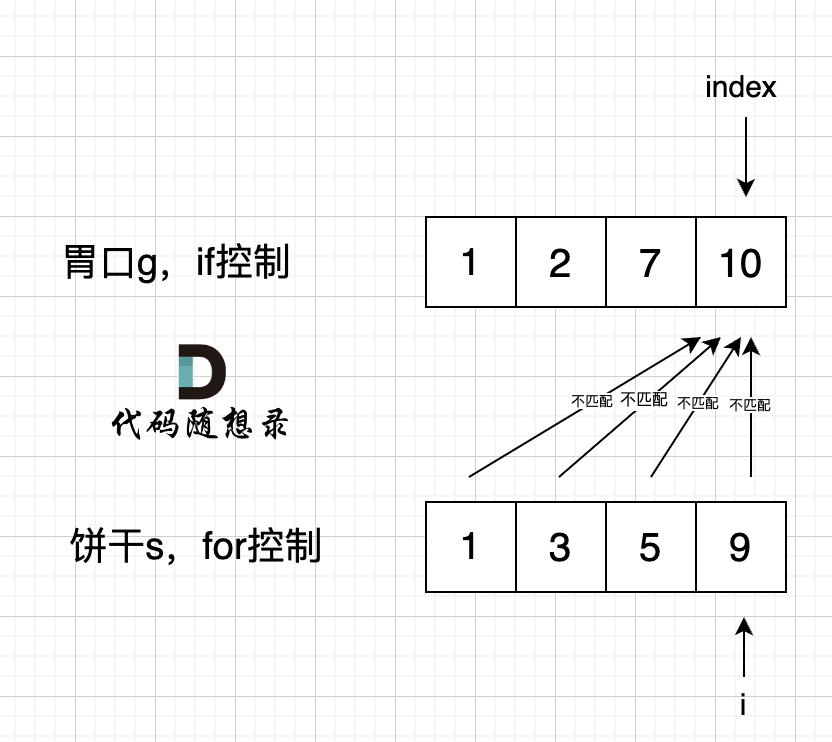
即，用饼干去遍历胃，有可能被最大的那个胃卡住了，因为for循环控制遍历，会一直更新饼干，导致没有一个胃被分配了。而我的代码，是从饼干和胃的最大值开始移动的，当找到一个和饼干匹配的胃，那么饼干和胃一起移动，没找到说明是胃太大，那么就只移动饼干了，下面是代码：

我的代码（双指针法）：

class Solution {
    public int findContentChildren(int[] g, int[] s) {
        Arrays.sort(g);
        Arrays.sort(s);
        int gIndex = g.length - 1;
        int sIndex = s.length - 1;
        int count = 0;
        while(gIndex >= 0 && sIndex >= 0) {
            if(s[sIndex] >= g[gIndex]) {
                count++;
                gIndex--;
                sIndex--;
            }else {
                gIndex--;
            }
        }
        return count;
    }
}

376. 摆动序列

如果连续数字之间的差严格地在正数和负数之间交替，则数字序列称为 摆动序列。第一个差（如果存在的话）可能是正数或负数。仅有一个元素（输出1）或者含两个不等元素的序列（输出2）也视作摆动序列。

例如， [1, 7, 4, 9, 2, 5] 是一个 摆动序列 ，因为差值 (6, -3, 5, -7, 3) 是正负交替出现的。

相反，[1, 4, 7, 2, 5] 和 [1, 7, 4, 5, 5] 不是摆动序列，第一个序列是因为它的前两个差值都是正数，第二个序列是因为它的最后一个差值为零。
子序列 可以通过从原始序列中删除一些（也可以不删除）元素来获得，剩下的元素保持其原始顺序。

给你一个整数数组 nums ，返回 nums 中作为 摆动序列 的 最长子序列的长度 。

示例 1：

输入：nums = [1,7,4,9,2,5]
输出：6
解释：整个序列均为摆动序列，各元素之间的差值为 (6, -3, 5, -7, 3) 。
示例 2：

输入：nums = [1,17,5,10,13,15,10,5,16,8]
输出：7
解释：这个序列包含几个长度为 7 摆动序列。
其中一个是 [1, 17, 10, 13, 10, 16, 8] ，各元素之间的差值为 (16, -7, 3, -3, 6, -8) 。
示例 3：

输入：nums = [1,2,3,4,5,6,7,8,9]
输出：2

这道题，我思考的时候就是：如果前一个连续的差为正（负），那么更新front记录为负（正），表示下次必须遇到负（正），计数器count才自增。但最终写出来是错的，先上错误代码：

class Solution {
    public int wiggleMaxLength(int[] nums) {
        int count = 1;			// 计数器默认为1，因为无论如何都有1个
        if(nums.length == 1) {
            return count;
        }
        int slow = 0;			// 我用了一个快慢指针来移动，其实这也是我这题思路出错的关键
        int fast = 1;
        // 下面是确定序列中，第一个差值，我这题的思路中，必须知道第一个差值，才能继续，因为如果，第一个差值是正（负），那么就设置对应的front为true（false），这样就能正确的进入判断正负交替
        while(fast < nums.length && nums[fast] - nums[slow] == 0) {
            fast++;
        }
        if(fast == nums.length) {
            return count;
        }
        boolean front = nums[fast] - nums[slow] > 0 ? true : false;
        while(fast < nums.length) {
            int sum = nums[fast] - nums[slow];
            if(sum != 0) {
                if(sum > 0 && front) {
                    count++;
                    slow = fast;
                    fast++;
                    front = false;
                    continue;
                }else if(sum < 0 && !front) {
                    count++;
                    slow = fast;
                    fast++;
                    front = true;
                    continue;
                }
            }
            fast++;
        }
        return count;
        
    }
}

最终，提交，发现有一个测试用例过不去，如图：

观察输出，我这个题解的思路似乎是漏了哪些值，或者说，我的这个局部最优解，不能推出全局最优解，哪里出错了？仔细一看，其实是我一开始的思路就有bug，我的最优解，是连续的摆动子序列和，因为每次不符合要求的移动时，我只移动了fast，并没有移动slow，导致我最终的结果是连续的，这就导致没能完全AC这道题，而我改成无论如何，slow和fast都同时移动后，代码就能AC了，下面是代码：

我的代码：

class Solution {
    public int wiggleMaxLength(int[] nums) {
        int count = 1;
        if(nums.length == 1) {
            return count;
        }
        int slow = 0;
        int fast = 1;
        while(fast < nums.length && nums[fast] - nums[slow] == 0) {
            fast++;
        }
        if(fast == nums.length) {
            return count;
        }
        boolean front = nums[fast] - nums[slow] > 0 ? true : false;
        while(fast < nums.length) {
            int sum = nums[fast] - nums[slow];
            if(sum != 0) {
                if(sum > 0 && front) {
                    count++;
                    // System.out.println(nums[slow]);
                    front = false;
                }else if(sum < 0 && !front) {
                    // System.out.println(nums[slow]);
                    count++;
                    front = true;
                }
            }
            slow = fast;
            fast++;
        }
        return count;
        
    }
}

对比代码随想录里的代码，其实我的这个是有点丑的，对于特殊的开头，如：[2,2,5]这一类的做了特殊的处理，还有，交替判断上下坡，我用的是一个front来判断，代码随想录里用差值来判断还是非常妙的思想的，上一波代码随想录里的代码：

代码随想录代码：

class Solution {
    public int wiggleMaxLength(int[] nums) {
        if (nums.length <= 1) {
            return nums.length;
        }
        //当前差值
        int curDiff = 0;
        //上一个差值
        int preDiff = 0;
        int count = 1;
        for (int i = 1; i < nums.length; i++) {
            //得到当前差值
            curDiff = nums[i] - nums[i - 1];
            //如果当前差值和上一个差值为一正一负
            //等于0的情况表示初始时的preDiff
            if ((curDiff > 0 && preDiff <= 0) || (curDiff < 0 && preDiff >= 0)) {
                count++;
                preDiff = curDiff;
            }
        }
        return count;
    }
}

还有他这个用两个差值来判断上下坡的思路，对于开头的处理非常巧妙，思路有点类似与链表中虚拟一个头结点来复制删除，即：在开头虚拟想象一个值，想象出的这个值，能够帮助我们理解解决特殊用例，（点击跳转文章）

53. 最大子数组和

给你一个整数数组 nums ，请你找出一个具有最大和的连续子数组（子数组最少包含一个元素），返回其最大和。

子数组 是数组中的一个连续部分。

示例 1：

输入：nums = [-2,1,-3,4,-1,2,1,-5,4]
输出：6
解释：连续子数组 [4,-1,2,1] 的和最大，为 6 。
示例 2：

输入：nums = [1]
输出：1
示例 3：

输入：nums = [5,4,-1,7,8]
输出：23

直接上代码吧，思路写在代码里了。

我的代码：

class Solution {
    public int maxSubArray(int[] nums) {
        int max = nums[0];    // 初始时，默认最大值为第一个元素
        int sum = 0;
        for(int i = 0; i < nums.length; i++) {
            sum += nums[i];
            if(nums[i] > sum) {
            // 更新累加起点，也就是所谓的“贪心”，
            // “贪”的是这个开头，如果加完这个数，
            // 但是这个数还大于前面所有累加的和，那么以它为开头再开始累加后面的数
                sum = nums[i];
            }
            if(sum > max) {    // 更新最大值
                max = sum;
            }
        }
        return max;
    }
}