Leetcode：subset && Recursive Knowledge

给定一组不含重复元素的整数数组 nums，返回该数组所有可能的子集（幂集）。

说明：解集不能包含重复的子集。

示例:

输入: nums = [1,2,3]
输出:
[
  [3],
  [1],
  [2],
  [1,2,3],
  [1,3],
  [2,3],
  [1,2],
  []
]

解法一，使用库itertool中的combination（）库函数来求解，combination（nums，r）输出nums所有长度为r的子集的一个生成器。

class Solution:
    def subsets(self, nums: List[int]) -> List[List[int]]:
        res = []
        for i in range(len(nums)+1):
            for tmp in itertools.combinations(nums, i):
                res.append(tmp)
        return res

因为包括了空集，长度要包括0到N。又因为产生的是生成器，所以也需要遍历出给定长度下的所有的值

解法二，使用迭代的思想，每次迭代都利用字符串相加的特性来构成新迭代的字符串：

class Solution:
    def subsets(self, nums: List[int]) -> List[List[int]]:
        result = [[]]
        for i in nums:
            result = result + [[i]+temp for temp in result]
        return result

时间复杂度很高。

解法三，使用广度搜索DFS，利用回溯算法来求解，类似于：

 

 

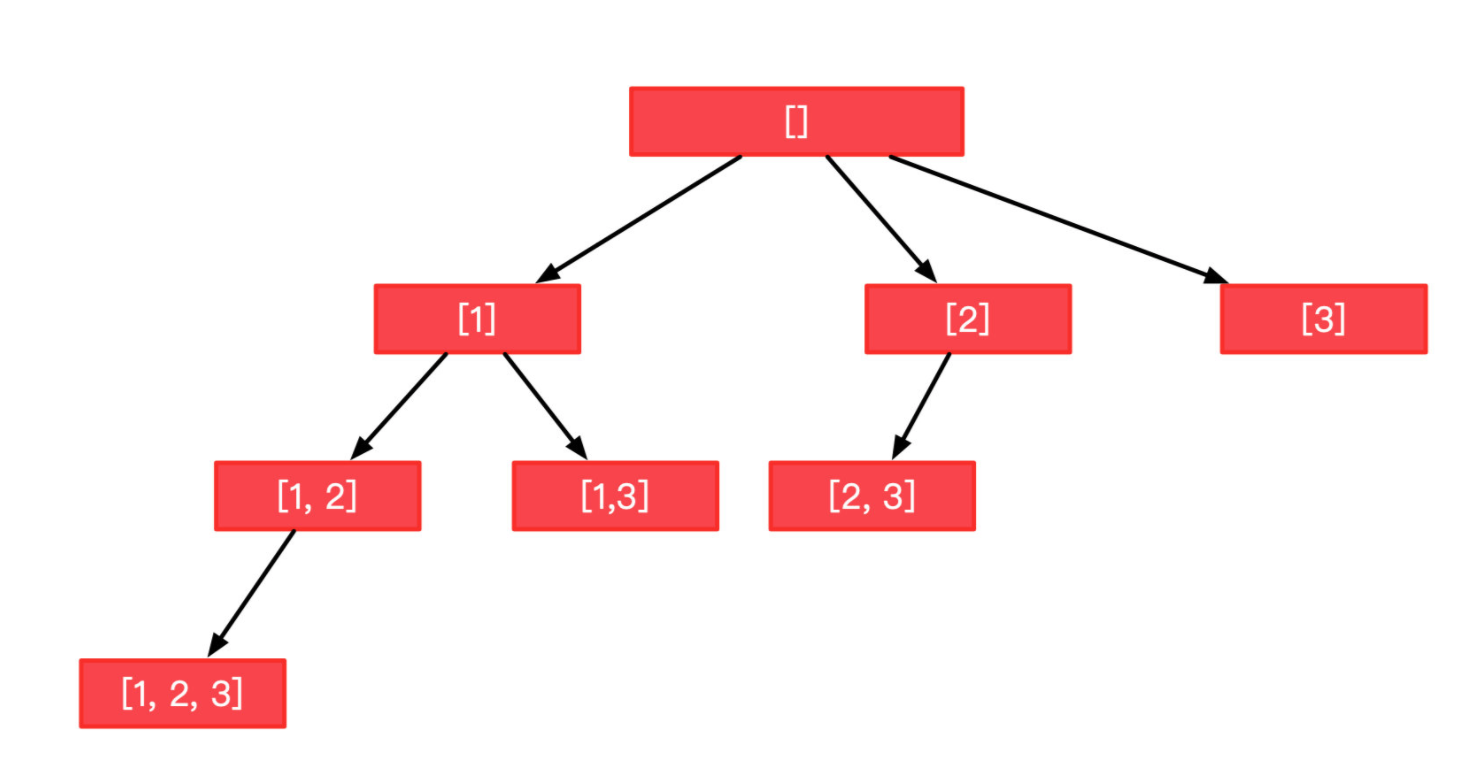
#based the DFS 
class Solution:
    def subsets(self, nums):
        size = len(nums)
        if size == 0:
            return []
        res = []
        self.__dfs(nums, 0, size, [], res)
        return res

    def __dfs(self, nums, start, size, path, res):
        res.append(path[:])
        for i in range(start, size):
            path.append(nums[i])
            # 因为 nums 不包  含重复元素，并且每一个元素只能使用一次
            # 所以下一次搜索从 i + 1 开始
            self.__dfs(nums, i + 1, size, path, res)
            path.pop

回溯算法这一块还没有理解的很到位，希望之后多做一些类似的题能够理解的更加到位。

解法四是使用编码的方式来求子集，如[0,0,0]代表空集，[0,0,1]代表子集{3}等：

class Solution:
    def subsets(self, nums: List[int]) -> List[List[int]]:
        size = len(nums)
        n = 1 << size
        res = []
        for i in range(n):
            cur = []
            for j in range(size):
                if i >> j & 1:
                    cur.append(nums[j])
            res.append(cur)
        return res

基本上摘抄于该题社区讨论中的解题思路。

 

学习了一下recursive递归的用法，稍微记录一下。

递归的定义：

Recursion is a method of solving problems that involves breaking a problem down into smaller and smaller subproblems until you get to a small enough problem that it can be solved trivially. Usually recursion involves a function calling itself. While it may not seem like much on the surface, recursion allows us to write elegant solutions to problems that may otherwise be very difficult to program.

所有的递归都服从三个原则：

1. A recursive algorithm must have a base case.
2. A recursive algorithm must change its state and move toward the base case.
3. A recursive algorithm must call itself, recursively.

第一条是一个递归算法必须含有一个最基本的问题，即能够分解成最小并容易求解的问题。

第二条是一个递归算法要改写它的表现形式，让其都能够向基本问题靠拢。

第三条是一个递归算法能够递归的去调用自己。

一个数组求和的简单例子：

def listsum(numList):
   if len(numList) == 1:
        return numList[0]
   else:
        return numList[0] + listsum(numList[1:])

print(listsum([1,3,5,7,9]))

其中的base case就是数组的长度递归到1；而改写的形式是让数组变短，让数组更加接近于基本问题；并且调用了本身。

第二个例子是10进制的数据在不同进制下的转换：

def toStr(n,base):
   convertString = "0123456789ABCDEF"
   if n < base:
      return convertString[n]
   else:
      return toStr(n//base,base) + convertString[n%base]

print(toStr(1453,16))

其中的base case就是数据要小于需要转化的进制；而改写的形式是对数据进行进制相除之后的整数部分；并且调用了本身。

第三个例子是对字符串进行反转：

from test import testEqual
def reverse(s):
    if len(s) <= 1:
        return s
    else:
        return reverse(s[1:]) + s[0]

其中的base case就是字符串的长度小于等于1，直接进行返回；而改写的形式是对字符串进行变短；并且调用了本身。

第四个列子是对回文的判断：

from test import testEqual
def removeWhite(s):
    ans = ''
    for ele in s:
        if  ele.isalpha()::
            ans = ans + ele
    return ans 

def isPal(s):
    if s == '':
        return True
    elif len(s) <= 3 :
        return s[0] == s[-1]
    else:
        return isPal(s[1:-1])

testEqual(isPal(removeWhite("x")),True)
testEqual(isPal(removeWhite("radar")),True)
testEqual(isPal(removeWhite("hello")),False)
testEqual(isPal(removeWhite("")

因为回文包括了句子，所以先定义个函数来去除字符串忠的空格和标点符号。

其中的base case就是当字符串的长度小于等于3时，判断两端是否相同；改写的形式就是去除掉判断完的两端数据，让字符串变短；并且调用了本身。

今天学到的简单递归知识，主要是来满足这三个条件，从而实现一些问题的求解。