算法解析：排序算法详解-优快云博客

本文链接：https://blog.youkuaiyun.com/remake_m/article/details/124219034

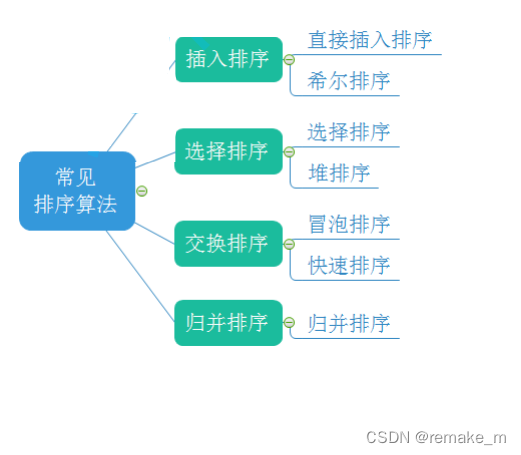
或许有的排序算法在生活中并不常用，但是学习他们往往会给我们日后的学习中提供思路。学习排序算法重要的不只是他们的思想，还有那些容易出问题的细节。掌握这些细节也就迈出了由我们脑海中的算法思想到代码实现的重要一步。

1.准备工作

Sort.h:

#include <stdio.h>
#include <stdlib.h>

//以升序为例

//1.插入排序
void InsertSort(int* a, int n);
//2.希尔排序
void ShellSort(int* a, int n);
//3.选择排序
void SelectSort(int* a, int n);
//4.堆排序
void HeapSort(int* a, int n);
//5.冒泡排序
void BubbleSort(int* a, int n);
//6.快速排序
void QuickSort(int* a ,int begin, int end);

void Print(int* a, int n);

void Sweap(int* pa, int* pb)
{
	int tmp = *pa;
	*pa = *pb;
	*pb = tmp;
}
void Print(int* a, int n)
{
	for (int i = 0; i < n; i++)
	{
		printf("%d ", a[i]);
	}
	printf("\n");
}

2.插入排序：

//插入排序
//直接排序
void InsertSort(int* a, int n)
{
	//i这里是小于n-1，因为如果i<n，a[end+1]就会出现越界访问
	for (int i = 0; i < n - 1; i++)
	{
		int end = i;
		int tmp = a[end + 1];
		while (end >= 0)
		{
			//tmp小于a[end]，那么a[end]往后挪一位覆盖掉end+1的位置。tmp在和end前一个位置比较
			if (tmp < a[end])
			{
				a[end + 1] = a[end];
				end--;
			}
			//直到tmp大于了a[end]就跳出了
			else
			{
				break;
			}
			//这里要注意不要写成下面注释的代码 
			//如:{100,2,....}这种情况，应该派成：{2，100，...}
			//但是end=0的时候发生if语句的操作之后，end = -1，while循环外面如果没有a[end + 1] = tmp;那么第一个位置就永远是100，2被删除了
/*			else
			{
				a[end + 1] = tmp;
				break;
			}*/	
		}
		a[end + 1] = tmp;
	}
}

3.希尔排序:

//希尔排序
//1.预排序 gap>1
//2.直接插入排序  gap==1
//gap越小越接近有序
//gap越大大的更快的到后面，小的更快的到前面，越不接近有序
//缺点：如果数据本身有序那么预排序无用，但是预排序本身很快。
void ShellSort(int* a, int n)
{
	//值得注意的是gap不能赋固定的值，如果gap=5，n=10万，那么效率会很低
	int gap = n ; 
	while (gap > 1)
	{
		//初始gap可以是 n / 3 + 1，也可以是n / 2 ;//+1是为了让gap=1便于进行直接插入排序
		gap = gap / 3 + 1;
		//循环条件是n-gap，要保证end+gap再数组范围内，可以参考InsertSort中的条件判断
		for (int i = 0; i < n-gap; i++)
		{
			int end = i;
			int tmp = a[end + gap];
			while (end >= 0)
			{
				if (tmp < a[end])
				{
					a[end + gap] = a[end];
					end -= gap;
				}
				else
				{
					break;
				}
			}
			a[end + gap] = tmp;
		}
	}
}

4.选择排序:

//选择排序  (优化后的)
void SelectSort(int* a, int n)
{
	int left = 0, right = n - 1;
	while (left < right)
	{
		int maxi = left, mini = left;
		//每次从i=left开始比，而不是i=0
		for (int i = left; i <= right; i++)
		{
			if (a[i] > a[maxi])
				maxi = i;
			if (a[i] < a[mini])
				mini = i;
		}
		Sweap(&a[left], &a[mini]);
		//如果a[left]是最大的那么一交换就把a[maxi]掉包了
		if (left == maxi)
		{
			maxi = mini;
		}
		Sweap(&a[right], &a[maxi]);
		left++, right--;
	}
}

5.堆排序:

//堆排序 
// 升序建大堆，降序建小堆
// 1.建大堆；2.排序
//第一次建的大堆是从倒数第一个双亲结点开始每个双亲结点都要建一次每次都到最后一个元素停止；
//第二次是每次都要从下标为0的位置建大堆到排好的元素前为止
void HeapSort(int* a, int n)
{
	//建大堆,
	
	//一共n个数，最后一个孩子的下标是n-1，所以最后一个双亲的下标是 : (最后一个孩子的下标-1)/2   ：(n-1-1)/2
	int parent = (n - 1 - 1) / 2;

	//让 从最后一个双亲节点开始往上的所有节点都是大堆，因为是从最后的双亲结点往上走所以循环条件是 parent>=0
	while (parent >= 0)
	{
		int child = parent * 2 + 1;

		//从双亲结点往下迭代 直到child>=n越了界了，就说明这个双亲结点下的数都排成大堆了
		while (child < n)
		{

			//从孩子中的选出最大的数和双亲结点比
			if (child + 1 < n && a[child + 1] > a[child])
			{
				child++;
			}

			//如果孩子大，就交换 并进行迭代
			if (a[child] > a[parent])
			{
				Sweap(&a[child], &a[parent]);
				parent = child;
				child = parent * 2 + 1;
			}
			//如果双亲结点大就说明大堆建好了，不用再迭代了
			else
			{
				break;
			}
		}
		parent--;
	}


	for (int j = n - 1; j > 0; j--)
	{
			//交换
			Sweap(&a[0], &a[j]);//把堆顶的元素和a[j]交换，这样大的数就归位了，现在要派的数就少一个
			//从下标为0开始建大堆
			int parent = 0;
			int child = parent * 2 + 1;
			//注意这里边界条件是 child<j 是随着排好的数的个数变化的
			while (child < j)
			{
				if (child + 1 < j && a[child + 1] > a[child])
				{
					child++;
				}
				if (a[child] > a[parent])
				{
					Sweap(&a[child], &a[parent]);
					parent = child;
					child = parent * 2 + 1;
				}
				else
				{
					break;
				}
			}
	}
}

6.冒泡排序:

//冒泡排序
//冒泡排序是最挫的（没优化的选择排序除外），与时间复杂度相同的插入排序相比还是挫不少，因为插入排序如果有一段是有序的，那么也会剩下很多时间
void BubbleSort(int* a, int n)
{
	//拍好n-1个数就拍好了整个数组
	for (int j = 0; j < n - 1; j++)
	{
		
		int flag = 0;
		//因为循环了j趟就拍好了j个数 ，那么只需要比较剩下的n-j个数就好了,也就是一共比较n-1-j次。如:j=0(第一趟)，只要比较n-1次；j=1(第二趟),只要比n-1-1次。
		for (int i = 0; i < n - 1 - j; i++)
		{
			if (a[i] > a[i + 1])
			{
				Sweap(&a[i], &a[i + 1]);
				flag = 1;
			}
		}
		if (flag == 0)
			break;
	}
}

快排是重中之重单独成篇。下一篇将重点讲述快排的思想和几种重要而且常考的实现方法。