第21章 电荷和电场
21.1 电荷(通过一些基础实验来用自然语言描述正电荷、负电荷)
# 电荷的基本一些性质:同性相斥、异性相吸;(玻璃棒和动物皮毛相互摩擦、激光打印)
# 电荷和物质的结构:原子的基本结构:原子核和和外电子(以及它们的尺度大小、质量大小、带电荷情况
Li元素、Li阳离子、Li阴离子)
# 电荷守恒定律、电荷量量子化、电荷的相对论不变性;
21.2 导体、半导体、绝缘体
#
21.3 库仑定律
# 库仑定律的论述:相对于惯性系观察,自由空间(或真空)中两个静止的点电荷之间的作用力(斥力或吸力,统称为库仑力)与这两个电荷所带电量的乘积成正比,与它们之间距离的平方成反比,作用力的方向沿着这两个点电荷的连线。同号电荷相斥,异号电荷相吸。
# 实验的精确度

# 例题
# 静电力的体现
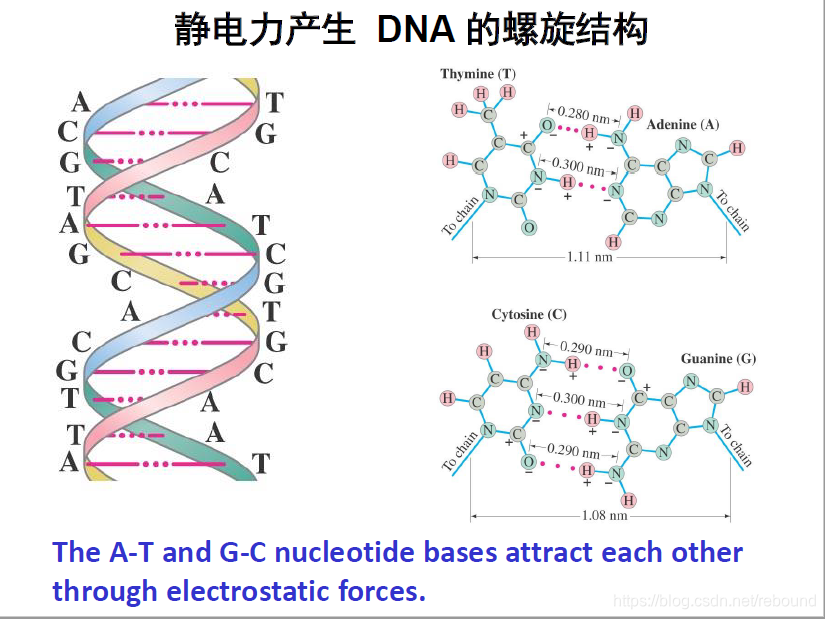
例题2
# 库仑定律的成立条件



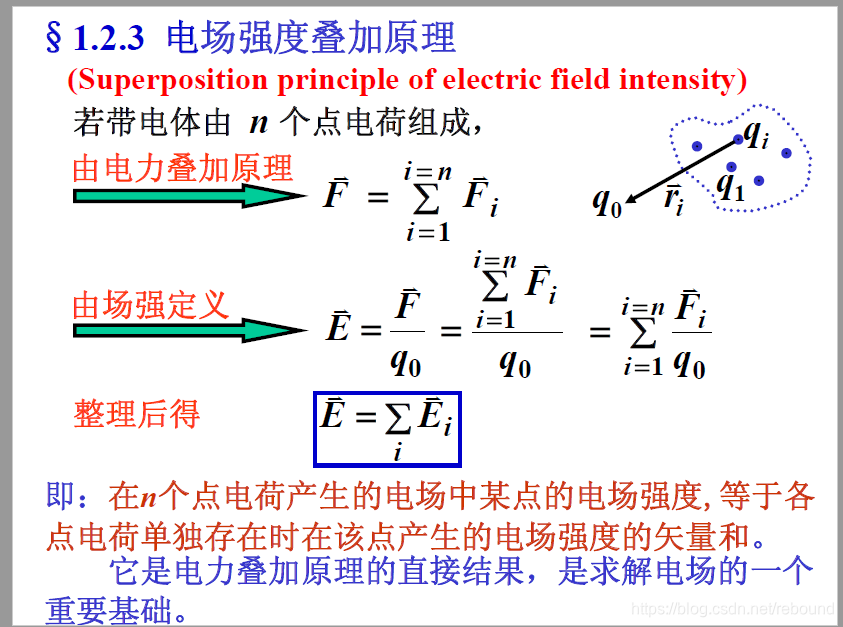
# 电场力的可叠加性


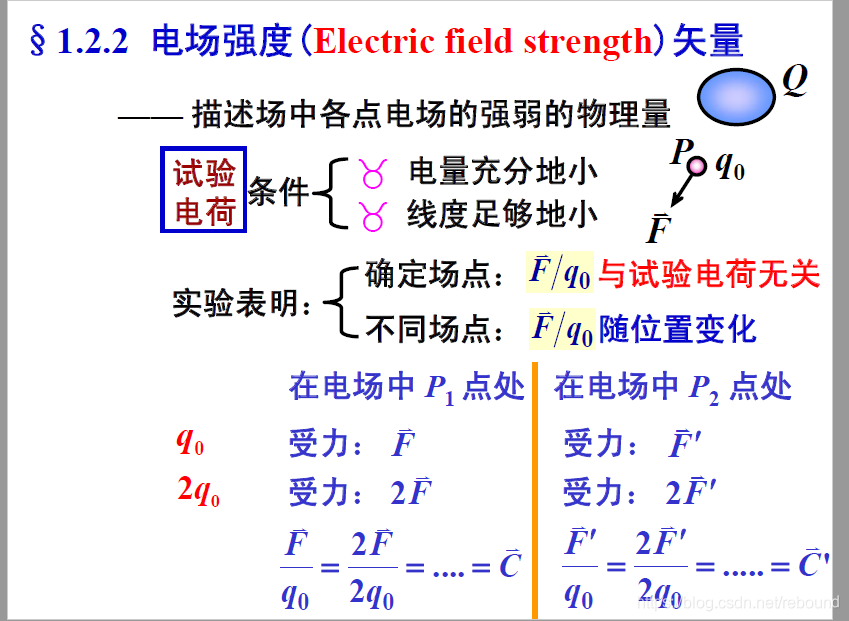
21.4 电场和电场力


21.5 电场叠加原理
21.6 电场线
21.7 电偶极子的性质

2、中轴线上
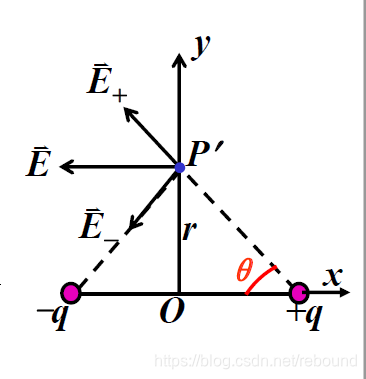


*21.8 电荷连续分布的带电体场强(额外的内容,需要有积分的基础知识储备,如果有问题,我会重新帮助复习一遍积分)
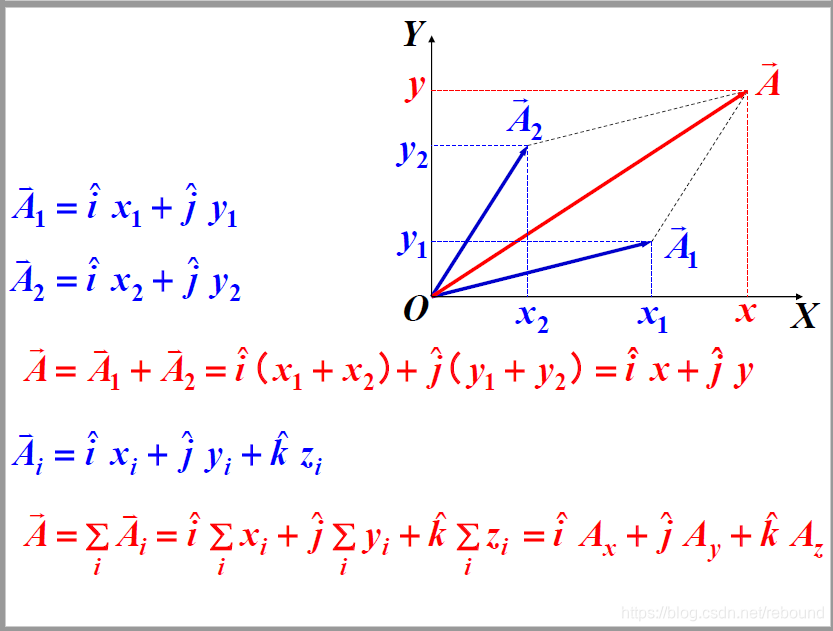
21.8.1 对电荷连续分布的带电体的场强(矢量积分就是先分解成空间三个互相垂直的分量,并进行标量积分,而后再将积分后的分量汇总)

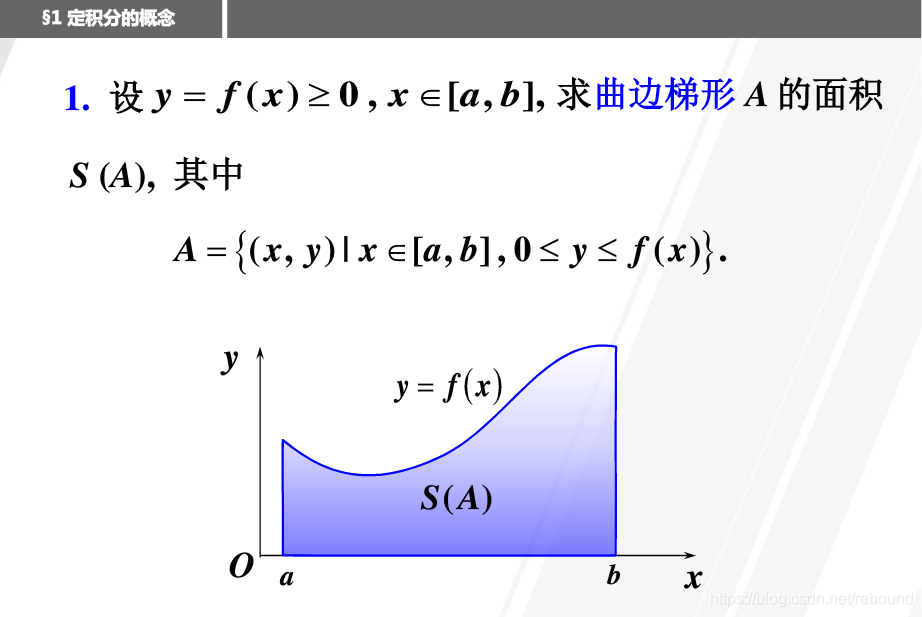

21.8.2 我们在二维坐标当中先行做一个小的测验,而在三维的情况下,考虑问题的角度是一致的;
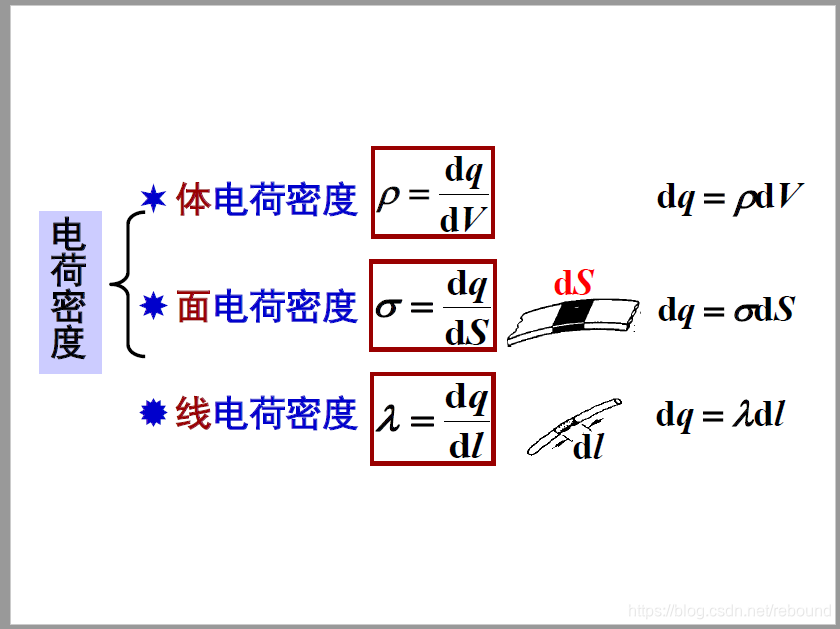
21.8.3 我们总是从简单的模型入手,在我们考虑简单的情形下,均匀分布是最easy的条件,所以让一个区域总的带电量平均分布,就形成了我们的线密度、面密度和体密度,这些概念的思想可以对照物质密度的定义
经典例题:

其长度为l,其线密度为η,求由该带点棒产生的场强在空间的分布情况?(理解场的分布就是一个矢量函数)
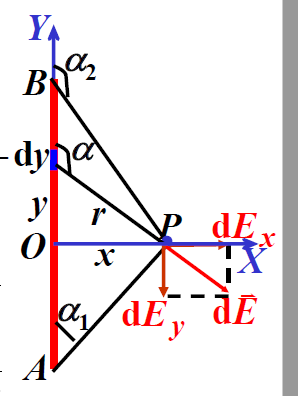
考虑两种特殊的情况:
1、当点落在x轴上时?
2、当长度l趋近无穷的时候?

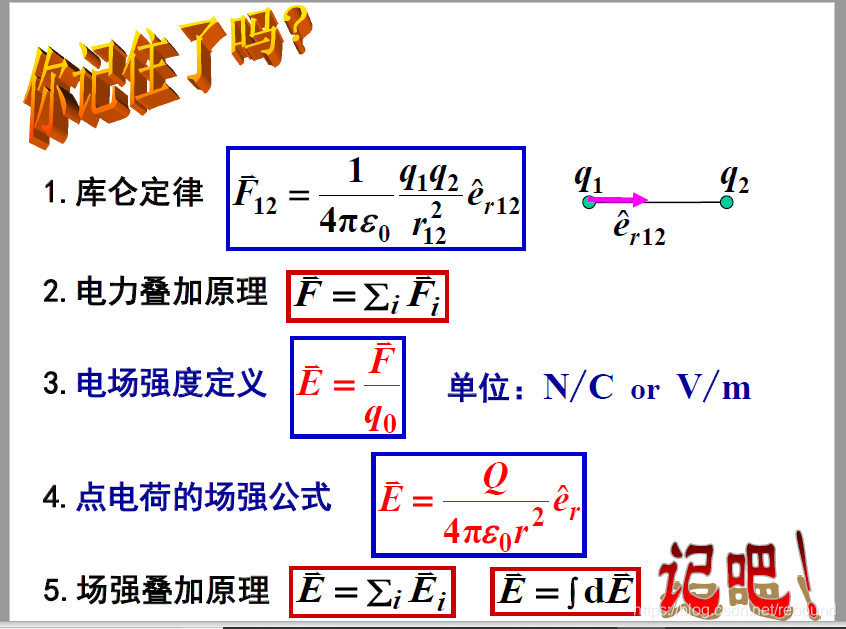







 博客围绕电荷和电场展开,介绍了电荷的基本性质、守恒定律等,阐述导体、半导体、绝缘体概念。重点讲解库仑定律,包括论述、实验精确度、成立条件等,还涉及电场和电场力、叠加原理等知识,最后给出电荷连续分布带电体场强的例题。
博客围绕电荷和电场展开,介绍了电荷的基本性质、守恒定律等,阐述导体、半导体、绝缘体概念。重点讲解库仑定律,包括论述、实验精确度、成立条件等,还涉及电场和电场力、叠加原理等知识,最后给出电荷连续分布带电体场强的例题。



















 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








