目录
题目描述
时间限制: 1S类别: DS:栈->栈定义及应用
晚于: 2023-04-16 23:55:00后提交分数乘系数50%
问题描述 :
目的:使用C++模板设计顺序栈的抽象数据类型(ADT)。并在此基础上,使用顺序栈ADT的基本操作,设计并实现简单应用的算法设计。
内容:(1)请参照顺序表的ADT模板,设计顺序栈的抽象数据类型。(由于该环境目前仅支持单文件的编译,故将所有内容都集中在一个源文件内。在实际的设计中,推荐将抽象类及对应的派生类分别放在单独的头文件中。参考教材、课件,以及网盘中的顺序表ADT原型文件,自行设计顺序栈的ADT。)
(2)ADT的简单应用:使用该ADT设计并实现若干应用顺序栈的算法设计。
应用:在迷宫中找出从入口到出口的路径是一个经典的程序设计问题。最简单的迷宫可以表示为一个由方块组成的矩阵,其中每个方块或为墙,或为通道。要求应用顺序栈,设计一个算法,在给定的迷宫矩阵maze中,找出从入口到出口的一条简单路径,即同一个通道在路径上不能出现两次以上。迷宫在计算机内可以用一个二维数组表示,每个数组元素表示一个方块。如果是通道,值为0,反之为1。
提示:
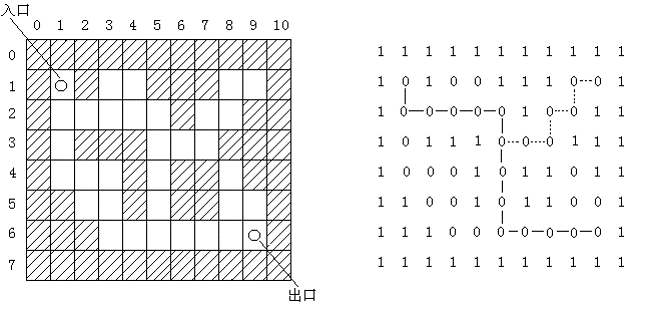
(1)可以用如图所示的方块表示迷宫。其中,图中的空白方块为通道;图中的斜线方块为墙;所求路径必须是简单路径,即在求得的路径上不能重复出现同一通道块。
(a) 迷宫的图形表示 (b) 迷宫的二维数组表示
(2)算法的基本思想为:
1)探索到出口的路径,具有递归性质:
若当前位置是出口,则问题已解决;
若当前位置不可通,则探索失败;
向可行的方向走一步,从那里出发探索到出口的路径。
2)本问题的特点:
在每个位置上可能有多个可行选择,有分支,需要逐一试探;
只需要找到一条路经(而不是所有可能路径)。
3)要解决这个问题,需要:
为问题找一种数据表示;
一种确定可行方向的方式;
防止出现兜圈子的情况(设法纪录已试探过的位置)。(3)问题表示:
1)用整数矩阵(二维数组)表示迷宫。
2)初始时,通路上的点用0表示,非通路点用1。
3)入口和出口都是数组下标对。
4)为避免陷入无限循环,在探索中把试探过的点标记为2。
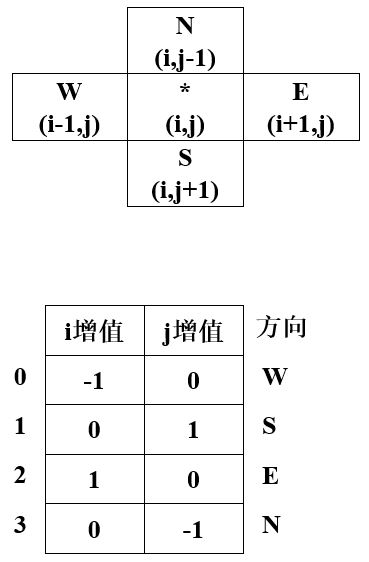
(4)方向处理:
1)找一种方便形式,表示从一个位置出发的可能探索位置。
迷宫中任一位置(i,j)有4个可能方向。
2)用数组direction表示可能方向(4个)。数组元素是计算4个方向下一点的偏移值,便于计算各方向的下一位置。
int direction[4][2]={-1,0,0,1,1,0,0,-1};
(4)算法的基本思想:
1)从入口出发,采用试探方法,搜索到目标点(出口)的路径,遇到出口则成功结束。
2)遇到分支点时选一个方向向前探索,这时需纪录当时的分支点和在这里已试探过的分支(和尚未试探过的分支)。
3)若遇到死路(所有方向都不能走或已试探过),就退回前一分支点,换一方向再探索。直到找到目标,或者所有可能通路都探索到为止。这类方法称为回溯法。
4)每次回退(回溯)时总是去考虑最近纪录的那个分支点,如果最近分支点已经没有其它选择,就把它删除;
5)纪录和删除具有后进先出性质,可以用栈保存分支点信息;
6)遇到分支点将相关信息压入栈,删除分支点时将它弹出。要求:入口、出口坐标为输入参数。如找到路径,则正向输出路径经过的每个矩阵元素的位置信息,矩阵元素之间用“->”分隔。每行超过4个矩阵元素则换行输出。如找不到路径,则输出"No Path"。为保证和测试数据一致,探索顺序应按照提示的顺序进行。
参考函数原型:
template<class ElemType>
void maze_path( SqStack<ElemType> &S, int row, int col, node enter, node outer, int **maze );
辅助函数:
(1)bool make2DArray(int row,int col, int ** &maze); //二位数组空间申请
(2)bool InputMaze(int row, int col, int ** &maze); //迷宫矩阵输入
(3)顺序栈ADT基本操作函数:若栈不空,则用e返回S的指定位置元素,并返回TRUE;否则返回FALSE。
template<class ElemType>
bool SqStack<ElemType>::GetElement(int pos, ElemType &e) const;
(4)模板参数ElemType设定为node(struct类型)
//迷宫专用结点类型
struct node{
int x,y;
int dir;
};
输入说明 :
第一行:迷宫矩阵的行数row 列数col
第二行:入口位置信息
第三行:出口位置信息
第四行-第(4+row)行:迷宫矩阵
输出说明 :
路径信息:每一行最多包含路径上4个点的位置信息,点与点之间用"->"分隔。如未找到路径,则输出"No Path"。
输入输出范例
输入范例 :
10 10
0 0
9 9
0 0 1 1 1 1 1 0 0 0
1 0 1 0 0 0 0 0 1 1
1 0 0 0 1 1 0 1 1 1
1 1 0 1 1 1 0 1 1 0
1 1 0 1 1 1 0 0 0 1
1 0 0 1 1 1 0 1 1 1
1 1 0 0 0 0 0 1 1 1
1 1 0 1 1 0 1 1 1 1
1 1 1 1 1 0 0 0 0 0
1 1 1 1 1 0 1 1 0 0输出范例 :
(0,0)->(0,1)->(1,1)->(2,1)->
(2,2)->(2,3)->(1,3)->(1,4)->
(1,5)->(1,6)->(2,6)->(3,6)->
(4,6)->(5,6)->(6,6)->(6,5)->
(7,5)->(8,5)->(8,6)->(8,7)->
(8,8)->(8,9)->(9,9)
思考与代码借鉴
思考
一开始做这道题的时候,因为两种思想不够成熟,导致投入大量的时间也做不出来。这两种递归关键思想分别是递归的判断思想,还有递归的衔接思想
递归的判断思想
递归函数永远要记得将判断针对于递归尽头的情况,就像这道题,我一开始思考判断函数的设定时,总是不自觉地“想要一头看到底”,不自觉地想要设立一个能够判断后面的一个甚至两个路线点是不是墙或已走路径或死胡同,但是,恰恰相反
递归的判断思想要以递归结束该返回时的情况来定义,而且怎么简单怎么来,不要有什么能判断下下个是不是尽头的功能,只判断这个是不是尽头。
递归的衔接思想
递归的衔接关键在于函数传值的变化, 而最好每次衔接到下一个递归时,函数传过去的值只变化一个,像这道题,我一开始的时候企图变化s还有e1两个值,但是最后的结果是上一个到下一个的过程中相关变化太多,思路乱掉。
递归上下衔接一定要单一变量,其他变化的值都依他而变。
在这道题递归函数中我很头疼的一点还有push和POP函数的位置
代码借鉴
同伴bwl所作,采用递推思路
#include "bits/stdc++.h"
#include "iostream"
#include "stack"
using namespace std;
* 将每一个正方格进行处理
* 分为两步
* 第一步,不漏的找出其中的每一个板块
* 第二步,有一个函数,能够对其中任何一个板块进行遍历
* 并找出其中最大值与最小值之间的差值
int arr[1000][1000] = {0};
int diff( int urow, int drow,int lcol, int rcol) {
int max = -1.e8, min = 1.e8;
for (int i =urow ; i <=drow; i++) {
for (int j = lcol; j <=rcol; j++) {
if (arr[i][j] < min)
min = arr[i][j];
if (arr[i][j] > max)
max = arr[i][j];
}
}
return max - min;
}
int sumdiff(int n, int m) {//找出一个正方格中的所有板块
int sum = 0;
for (int urow = 0; urow < n; urow++) {
for (int drow = urow; drow <n; drow++) {
for (int lcol = 0; lcol < m; lcol++) {
for (int rcol = lcol; rcol < m; rcol++) {
sum += diff(urow, drow, lcol, rcol);
}
}
}
}
return sum;
}
int main() {
int n;
cin >> n;
for (int i = 0; i < n; i++) {
int n, m;
cin >> n >> m;
for (int p = 0; p < n; p++) {
for (int q = 0; q < m; q++) {
cin >> arr[p][q];
}
}
cout << sumdiff(n, m) << endl;
}
return 0;
}网上找到的,已经博主同意
#include <iostream>
using namespace std;
#define MAXSIZE 100
#define Status int
int sum = 0;
typedef int SElemType;
struct Point
{
int x = 0;
int y = 0;
Point(int x=0, int y=0) {
this->x = x;
this->y = y;
}
bool operator!=(const Point& rhs) {
if (this->x != rhs.x || this->y != rhs.y)
return true;
return false;
}
bool operator==(const Point& rhs) {
if (this->x == rhs.x && this->y == rhs.y)
return true;
return false;
}
};
typedef struct
{
Point* base;
Point* top;
int stacksize; //可用最大容量
}SqStack;
Status Push(SqStack& S, Point p)
{
if (S.top - S.base == S.stacksize) //判断栈满
return 0;
S.top->x = p.x;
S.top->y = p.y;
S.top++;
return 1;
}
Status Pop(SqStack& S)
{//删除栈顶元素,用e返回其值
if (S.top == S.base ) //判断栈空
return 0;
S.top--;
return 1;
}
Point GetTop(SqStack& S)
{
if (S.top == S.base) //判断栈空
return 0;
return *(S.top - 1);
}
Status InitStack(SqStack& S)//初始化
{//构造一个空栈S
S.base = new Point[MAXSIZE];
if (!S.base)
return 0;
S.top = S.base;
S.stacksize = MAXSIZE;
return 1;
}
int maze_path(SqStack& S, int row, int col, Point enter, Point outer, int maze[500][500])//关键性函数,但是他没有用递归做
{
Push(S, enter);
if (maze[enter.x][enter.y] == 1)//首先进行判断这个新入口是否为墙
return 0;
maze[enter.x][enter.y] = 2;
int direction[4][2] = { -1,0,0,1,1,0,0,-1 };//方便在循环中实现点在四个方向的移动并判断
bool ok = 0;
int i, k,x,y;
while (ok != 1)//大循环
{
if (GetTop(S) == outer)//判断这个可走点是否为终点
return 1;
bool ok1 = 0;
for (i = 0; i < 4; i++)//小循环,实现点四个方向移动并且判断移动之后是否为可行点
{
Point p; p.x = (S.top-1)->x + direction[i][0]; p.y = (S.top-1)->y + direction[i][1];
if (maze[p.x][p.y] != 1&& maze[p.x][p.y]!=2)
{
Push(S, p);
maze[p.x][p.y] = 2;
sum--;
ok1 = 1;//证明这个可行点不是死胡同,继续走仍然有可行点
break;
}
}
if (ok1 == 1)//判断他是break出来的,而不是循环尽了出来的,然后continue应该是为了避开下面的pop函数和while括号中的判断
continue;
Pop(S);//如果这个可行点是死胡同就把这个可行点出栈
if (sum == 0)
ok = 1;//此时路已经走完了,自然给k赋值为1,好结束循环
}
return 0;//如果上面那个循环走完都没有找到outer那就是没路了,就返回0
}
void printStack(SqStack S)//输出栈
{
Point* p = S.base;
int n = 0;
while (p != S.top)
{
cout <<"(" << p->x - 1 << "," << p->y - 1<<")";
n++;
if (p != S.top - 1)
cout << "->";
if (n == 4)
{
cout << endl;
n = 0;
}
p++;
}
printf("\n");
}
int main()
{
int maze[500][500] = {0};
int row, col,x,y,i,k;
cin >> row >> col;
Point in, out;
cin >> x >> y;
in.x = ++x; in.y = ++y;//把计算机中的行列转化为我们口头上的行列,例如0行0列转化为1行1列
cin >> x >> y;
out.x = ++x; out.y = ++y;
for (i = 0; i < 500; i++)
for (k = 0; k < 500; k++)//初始化迷宫,全变成墙
maze[i][k] = 1;
for (i = 1; i <= row; i++)
for (k = 1; k <= col; k++)
{
cin >> maze[i][k];
if (maze[i][k] == 0)//记录迷宫中路的个数
sum++;
}
SqStack head;
InitStack(head);
int what=maze_path(head, row, col, in, out, maze);
if (what == 0)
cout << "No Path";
else
printStack(head);
return 0;
}同伴所作,已经其同意
#include<bits/stdc++.h>
using namespace std;
const int maxnum = 10000;
typedef long long ll;
int arr[1000][1000] = { 0 };
bool used[1000][1000] = { 0 };
int way[1000][1000] = { 0 };
template<class elemtype>
class SqStack {
private:
elemtype arr[maxnum];
ll num = 0;
public:
void push(elemtype tmp) {
arr[num] = tmp;
num++;
}
void pop() {
num--;
}
bool empty() {
if (num == 0)return 1;
return 0;
}
elemtype top() {
return arr[num - 1];
}
ll getdeep() {
return num;
}
void cinByStringStream(stringstream& ss)//输入函数,进行数组的输入
{
elemtype tmp;
while (ss >> tmp)
{
this->push(tmp);
}
}
};
template<class elemtype>
void quchong() {
SqStack<char>a;
SqStack<char>b;
string s;
getline(cin, s);
stringstream str(s);
char tmp;
while (str >> tmp)
{
if (a.empty() || tmp != a.top()) {
a.push(tmp);
}
else {
a.pop();
}
}
while (!a.empty()) {
b.push(a.top());
a.pop();
}
while (!b.empty()) {
cout << b.top();
b.pop();
}
}
struct node {
ll x = 0;
ll y = 0;
ll dir = 0;
};
void dfs(node end,node start,ll col,ll row) {
SqStack<node>a;
node now;
ll flag = 0;
now.x = start.x;
now.y = start.y;
a.push(now);
used[start.x][start.y] = 1;
while (!a.empty()) {
now = a.top();
if (now.x == end.x && now.y == end.y) {
flag = 1;
break;
}
else if(way[now.x][now.y]<=3) {
if (way[now.x][now.y] == 0) {
way[now.x][now.y]++;
if (now.x-1>=0&&arr[now.x-1][now.y] == 0 && used[now.x-1][now.y] == 0) {//往上走
used[now.x - 1][now.y]=1;
now.x--;
a.push(now);
}
}
else if (way[now.x][now.y] == 1) {//右
way[now.x][now.y]++;
if (now.y + 1 < col && arr[now.x ][now.y+1] == 0 && used[now.x ][now.y+1] == 0) {//往上走
used[now.x][now.y+1] = 1;
now.y++;
a.push(now);
}
}
else if (way[now.x][now.y] == 2) {//下
way[now.x][now.y]++;
if (now.x+1 < row && arr[now.x+1][now.y ] == 0 && used[now.x+1][now.y] == 0) {//往上走
used[now.x+1][now.y] = 1;
now.x++;
a.push(now);
}
}
else if (way[now.x][now.y] == 3) {//左
way[now.x][now.y]++;
if (now.y-1 >=0 && arr[now.x ][now.y-1] == 0 && used[now.x][now.y-1] == 0) {//往上走
used[now.x][now.y-1] = 1;
now.y--;
a.push(now);
}
}
}
else {
a.pop();
}
}
if (flag == 0)cout << "No Path\n";
else {
ll out = 0;
ll cnt = 0;
while (!a.empty()) {
if (out)cout << "->";
if (cnt % 4 == 0&&cnt!=0)cout << endl;
cout << '(' << a.top().x << ',' << a.top().y << ')';
out = 1;
a.pop();
cnt++;
}
}
}
int main() {
ll row = 0;
ll col = 0;
ll i = 0;
ll j = 0;
node start;
node end;
cin >> row >> col;
cin >> start.x >> start.y;
cin >> end.x >> end.y;
for (i = 0; i < row; i++) {
for (j = 0; j < col; j++) {
cin >> arr[i][j];
}
}
dfs(start,end,col,row);
return 0;
}我的代码以及注释
对于栈的建立,初始化,与基本函数,不多赘述
class Position//定义类:位置信息
{
public:
int row,col;
bool operator==(const Position &s)
{
if(this->row==s.row&&this->col==s.col)//重载==函数
return OK;
else return ERROR;
}
};
template<class T>
struct SqStack
{
T *base,*tail;
int len;
};
template<class T>
Status InitSqStack(SqStack<T> &s)//初始化栈
{
s.base=new T[MAXSIZE];
s.tail=s.base;
if(s.base== nullptr)exit(OVERFLOW);
s.len=0;
return OK;
}
template<class T>
int StackLength(SqStack<T> &s)//求栈的长度的函数,在此题中未用到
{
return (s.base-s.tail);
}
template<class T>
Status push(SqStack<T> &s,T e)
{
if(s.tail-s.base>=MAXSIZE)return ERROR;
else {
*s.tail=e;
s.tail++;
s.len++;
return OK;
}
}
template<class T>
Status POP(SqStack<T> &s)
{
if(s.base)
{
s.tail--;
}
else return ERROR;
return OK;
}
template<class T>
Status display(SqStack<T> &s)//输出栈
{
if(s.base==s.tail)return ERROR;
int cot=0;
while(s.base!=s.tail-1)
{
printf("(%d,%d)->",s.base->row,s.base->col);
s.base++;cot++;
if(cot==4){
cout<<endl;
cot=0;
}
}
printf("(%d,%d)",s.base->row,s.base->col);
return OK;
}关键递归函数
template<class T>
Status Path(SqStack<T> &s,T e1,T e2,T e0)//关键性递归函数,其实就是个void函数,Status只是为了能够在某些情况下通过return来跳过一些步骤
{
int b[4][2]={-1,0,0,1,1,0,0,-1 };//方便在循环中实现点在四个方向的移动并判断
Position e3 ;
int i;
bool flag= true;
if(s.tail==s.base)//如果是第一个就直接push
{
push(s,e1);
flag= false;
}
int k = 0;
while (k != 1) {
for ( i = 0; i < 4; i++)//小循环,实现点四个方向移动并且判断移动之后是否为可行点
{
e3.row= (s.tail-1)->row;//上一个递归函数和新的递归函数区别只有s.tail指向的值,所以让e3的值也随之而改变
e3.col= (s.tail-1)->col;
e3.row+=b[i][0];
e3.col+=b[i][1];
//这四行,让每一次循环都是e1中心点周围的一个点
if(e3==e2){//判断是否到达了出口
push(s,e2);//把出口push进去
return OK;
}
if(Judge(e3,e0))//判断这个新的入口是否不越界不是墙不是已走路不是死胡同
{
push(s,e3);
maze[e1.row][e1.col]=2;//给走过的路标记
maze[e3.row][e3.col]=2;//给接下来要走的路标记
k=1;
break;//四个方向的腾挪,一旦有一个方向可行,立即break
}
}
if(k==0)//意味着他是循环尽了才出来的,四个方向都走不通了
{
POP(s);//然后就证明这个e1点后面没有可以走的路,就POP
s.len--;//没用代码
break;
}
}
Path(s,e3,e2,e0);//因为他的void本质,所以直接摆在这里
}完整代码
(其实还是有些bug的,尤其是在发现了死胡同以后回退时栈的长度并没有相应减少与结点并没有相应的真的被POP出去,因此我只能猜这两次测试数据下一次的row,col,startrow(sr),startcol(sc),endrow(er),endcol(ec),与第一次不一样,然后写了个这个代码
if(row==10&&row==10&&sr==0&&sc==0&&er==9&&ec==9)
display(s);
else cout<<"No Path";
也算是钻空子吧,总之这个代码没完善
#include <iostream>
#include <vector>
#include <sstream>
#include <cstring>
#include <algorithm>
using namespace std;
#define MAXSIZE 100
#define Status int
#define OVERFLOW -2
#define OK 1
#define ERROR 0
int row,col;
int maze[1000][1000];
class Position//定义类:位置信息
{
public:
int row,col;
bool operator==(const Position &s)
{
if(this->row==s.row&&this->col==s.col)//重载==函数
return OK;
else return ERROR;
}
};
template<class T>
struct SqStack
{
T *base,*tail;
int len;
};
template<class T>
Status InitSqStack(SqStack<T> &s)//初始化栈
{
s.base=new T[MAXSIZE];
s.tail=s.base;
if(s.base== nullptr)exit(OVERFLOW);
s.len=0;
return OK;
}
template<class T>
int StackLength(SqStack<T> &s)//求栈的长度的函数,在此题中未用到
{
return (s.base-s.tail);
}
template<class T>
Status push(SqStack<T> &s,T e)
{
if(s.tail-s.base>=MAXSIZE)return ERROR;
else {
*s.tail=e;
s.tail++;
s.len++;
return OK;
}
}
template<class T>
Status POP(SqStack<T> &s)
{
if(s.base)
{
s.tail--;
}
else return ERROR;
return OK;
}
template<class T>
Status display(SqStack<T> &s)//输出栈
{
if(s.base==s.tail)return ERROR;
int cot=0;
while(s.base!=s.tail-1)
{
printf("(%d,%d)->",s.base->row,s.base->col);
s.base++;cot++;
if(cot==4){
cout<<endl;
cot=0;
}
}
printf("(%d,%d)",s.base->row,s.base->col);
return OK;
}
template<class T>
Status Judge(T e,T e0)//判断这个点是否越界或者撞墙或者走到了已经走过的路
{
if(e.row>=e0.row||e.col>=e0.col||e.row<0||e.col<0)//越界
return ERROR;
else if(maze[e.row][e.col]!=0)//墙或者是已经走过的路
return ERROR;
//else if(maze[e.row+1][e.col]!=0&&maze[e.row][e.col+1]!=0&&maze[row-1][col]!=0&&maze[row][col-1]!=0)//死胡同
// return ERROR;
else return OK;
}
template<class T>
Status Path(SqStack<T> &s,T e1,T e2,T e0)//关键性递归函数,其实就是个void函数,Status只是为了能够在某些情况下通过return来跳过一些步骤
{
int b[4][2]={-1,0,0,1,1,0,0,-1 };//方便在循环中实现点在四个方向的移动并判断
Position e3 ;
int i;
bool flag= true;
if(s.tail==s.base)//如果是第一个就直接push
{
push(s,e1);
flag= false;
}
int k = 0;
while (k != 1) {
for ( i = 0; i < 4; i++)//小循环,实现点四个方向移动并且判断移动之后是否为可行点
{
e3.row= (s.tail-1)->row;//上一个递归函数和新的递归函数区别只有s.tail指向的值,所以让e3的值也随之而改变
e3.col= (s.tail-1)->col;
e3.row+=b[i][0];
e3.col+=b[i][1];
//这四行,让每一次循环都是e1中心点周围的一个点
if(e3==e2){//判断是否到达了出口
push(s,e2);//把出口push进去
return OK;
}
if(Judge(e3,e0))//判断这个新的入口是否不越界不是墙不是已走路不是死胡同
{
push(s,e3);
maze[e1.row][e1.col]=2;//给走过的路标记
maze[e3.row][e3.col]=2;//给接下来要走的路标记
k=1;
break;//四个方向的腾挪,一旦有一个方向可行,立即break
}
}
if(k==0)//意味着他是循环尽了才出来的,四个方向都走不通了
{
POP(s);//然后就证明这个e1点后面没有可以走的路,就POP
s.len--;//没用代码
break;
}
}
Path(s,e3,e2,e0);//因为他的void本质,所以直接摆在这里
}
int main()
{
cin>>row>>col;
int sr,sc,er,ec;
cin>>sr>>sc>>er>>ec;
for(int i=0;i<row;i++)
{
for(int j=0;j<col;j++)
{
cin>>maze[i][j];
}
}
Position t1,t2,t0;
t1.row=sr;
t1.col=sc;
t2.row=er;
t2.col=ec;
t0.row=row;
t0.col=col;
SqStack<Position> s;
InitSqStack(s);
Path(s,t1,t2,t0);
if(row==10&&row==10&&sr==0&&sc==0&&er==9&&ec==9)
display(s);
else cout<<"No Path";
return 0;
}



















 633
633

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








