无重复字符的最长子串 - LeetCode 刷题解析

无重复字符的最长子串 - LeetCode 刷题解析

整套题解详见 https://rscai.github.io/leetcode-bytedance/zh_CN/

题目

给定一个字符串，请你找出其中不含有重复字符的 最长子串 的长度。

示例 1:

输入: "abcabcbb"
输出: 3
解释: 因为无重复字符的最长子串是 "abc"，所以其长度为 3。

示例 2：

输入: "bbbbb"
输出: 1
解释: 因为无重复字符的最长子串是 "b"，所以其长度为 1。

示例 3：

输入: "pwwkew"
输出: 3
解释: 因为无重复字符的最长子串是 "wke"，所以其长度为 3。
    请注意，你的答案必须是 子串 的长度，"pwke" 是一个子序列，不是子串。

枚举法

枚举所有子串，再逐一检测其是否包含重复元素。

代码实现

package io.github.rscai.leetcode.bytedance.string;

import java.util.HashSet;
import java.util.Set;

public class Solution1012A {

  public int lengthOfLongestSubstring(String s) {
    int maxLength = 0;
    for (int start = 0; start < s.length(); start++) {
      for (int end = start + 1; end <= s.length(); end++) {
        if (isUnique(s.substring(start, end)) && (end - start) > maxLength) {
          maxLength = end - start;
        }
      }
    }
    return maxLength;
  }

  private boolean isUnique(String s) {
    Set<Character> containedChars = new HashSet<>();
    for (Character ch : s.toCharArray()) {
      if (containedChars.contains(ch)) {
        return false;
      }
      containedChars.add(ch);
    }
    return true;
  }
}

使用两重循环枚举所有子串。

然后逐一检测子串，判断其是否不包含重复字符且长度大于已知最大不重复子串。

在HashSet的帮助下，可以在常数复杂度内完成不包含重复字符检测。

复杂度分析

时间复杂度分析

本演算法要遍历所有子串的所有字符。将子串长度记为起止点的函数$$len(s,e)=e-s$$，所有子串长度和为$$\sum _{s=0}^{n-1}\sum _{e=s+1}^n(e-s)$$。时间复杂度为

$$\begin{array}{rl}{C}_{time}& =\mathcal{O}(\sum _{s=0}^{n-1}\sum _{e=s+1}^n(e-s))\\ & =\mathcal{O}(\sum _{s=0}^{n-1}\frac{(1+n-s)(n-s)}{2})\\ & =\mathcal{O}(n^3)\end{array}$$

空间复杂度分析

在检测子串是否包含重复字符时使用了HashSet去存储子串中所有字符，其最大佔用空间等于最中子串长度$$n$$。所以空间复杂度为$$\mathcal{O}(n)$$。

动态规划法

动态规划

动态规划（英语：Dynamic programming，简称DP）是一种在数学、管理科学、电脑科学、经济学和生物资讯学中使用的，通过把原问题分解为相对简单的子问题的方式求解复杂问题的方法。

动态规划常常适用于有重叠子问题和最佳子结构性质的问题，动态规划方法所耗时间往往远少于朴素解法。

动态规划背后的基本思想非常简单。大致上，若要解一个给定问题，我们需要解其不同部分（即子问题），再根据子问题的解以得出原问题的解。

通常许多子问题非常相似，为此动态规划法试图仅仅解决每个子问题一次，从而减少计算量：一旦某个给定子问题的解已经算出，则将其记忆化储存，以便下次需要同一个子问题解之时直接查表。这种做法在重复子问题的数目关于输入的规模呈指数增长时特别有用。

概述

动态规划在寻找有很多重叠子问题的情况的最佳解时有效。它将问题重新组合成子问题。为了避免多次解决这些子问题，它们的结果都逐渐被计算并被储存，从简单的问题直到整个问题都被解决。因此，动态规划储存递回时的结果，因而不会在解决同样的问题时花费时间。

动态规划只能应用于有最佳子结构的问题。最佳子结构的意思是局部最佳解能决定全域最佳解（对有些问题这个要求并不能完全满足，故有时需要引入一定的近似）。简单地说，问题能够分解成子问题来解决。

适用情况

1. 最佳子结构性质。如果问题的最佳解所包含的子问题的解也是最佳的，我们就称该问题具有最佳子结构性质（即满足最佳化原理）。最佳子结构性质为动态规划演算法解决问题提供了重要线索。
2. 无后效性。即子问题的解一旦确定，就不再改变，不受在这之后、包含它的更大的问题的求解决策影响。
3. 子问题重叠性质。子问题重叠性质是指在用递回演算法自顶向下对问题进行求解时，每次产生的子问题并不总是新问题，有些子问题会被重复计算多次。动态规划演算法正是利用了这种子问题的重叠性质，对每一个子问题只计算一次，然后将其计算结果储存在一个表格中，当再次需要计算已经计算过的子问题时，只是在表格中简单地检视一下结果，从而获得较高的效率。

参考

• 动态规划
• Dynamic Programming

将所有子串以树的形式展现，从根节点到叶子节点的路径为子串，所有的路径组成了所有子串集合。

可以直观地发现有很多重叠的子树，即有很多子串是重叠的。这些重叠的子树就是可以优化的「重叠子问题」。

无重复字符子串的判定可以以递归的形式描述为：

i s U n i q u e ( s , e ) = c h a r s ∉ { c h a r s + 1 , . . . , c h a r e } ∧ i s U n i q u e ( s + 1 , e ) isUnique(s,e) = char_s \notin \{char_{s+1}, ..., char_e\} \land isUnique(s+1,e) isUnique(s,e)=chars​∈/​{chars+1​,...,chare​}∧isUnique(s+1,e)

若以s+1为起始、以e为截止的子串无重复子符且第s个字符未在s+1至e之间出现，则以s为起始、以e为截止的子串不包含重复字符。

代码实现

package io.github.rscai.leetcode.bytedance.string;

import java.util.Arrays;
import java.util.Collections;
import java.util.HashMap;
import java.util.HashSet;
import java.util.List;
import java.util.Map;
import java.util.Set;
import java.util.function.BiFunction;

public class Solution1012B {

  public int lengthOfLongestSubstring(String s) {
    BiFunction<Integer, Integer, Boolean> isUnique = new BiFunction<Integer, Integer, Boolean>() {
      private Map<List<Integer>, Boolean> cachedAnswers = new HashMap<>();
      private Map<List<Integer>, Set<Character>> charSets = new HashMap<>();

      @Override
      public Boolean apply(Integer start, Integer end) {
        List<Integer> key = Arrays.asList(start, end);
        if (end <= start) {
          charSets.put(key, Collections.emptySet());
          return true;
        }
        if (cachedAnswers.containsKey(key)) {
          return cachedAnswers.get(key);
        }
        return doApplyAndCache(start, end);
      }

      private boolean doApplyAndCache(Integer start, Integer end) {
        List<Integer> key = Arrays.asList(start, end);
        List<Integer> subQuestionKey = Arrays.asList(start + 1, end);
        boolean result =
            apply(start + 1, end) && !charSets.get(subQuestionKey).contains(s.charAt(start));
        if (result) {
          Set<Character> charSet = new HashSet<>(charSets.get(subQuestionKey));
          charSet.add(s.charAt(start));
          charSets.put(key, charSet);
        }
        return result;
      }
    };
    int maxLength = 0;
    for (int start = 0; start < s.length(); start++) {
      for (int end = start + 1; end <= s.length(); end++) {
        if (isUnique.apply(start, end)) {
          maxLength = Math.max(maxLength, end - start);
        }
      }
    }
    return maxLength;
  }
}

首先，与暴力法相同，枚举所有子串。

然后，逐一检测是否包含重复字符。若无且子串长度大于已知最大无重复字符子串长度，则更新之。

使用慝名函数对象实现带缓存值功能的isUnique函数。该函数缓存了两类值：是否包含重复子串和子串字符集合。该函数首先检查是否已缓存值，是则返回缓存的值，无需重复计算。

若无缓存值则计算之。根据公式 i s U n i q u e ( s , e ) = c h a r s ∉ { c h a r s + 1 , . . . , c h a r e } ∧ i s U n i q u e ( s + 1 , e ) isUnique(s,e) = char_s \notin \{char_{s+1}, ..., char_e\} \land isUnique(s+1,e) isUnique(s,e)=chars​∈/​{chars+1​,...,chare​}∧isUnique(s+1,e)，先计算子串(start+1, end)是否包含重复字符，再检测在start位置的字符是否已在子串(start+1,end)串出现过。若两则皆为否，则该子串不包含重复字符。

若某一子串不包含重复字符，则应缓存其字符集合，以便后续使用。

复杂度分析

时间复杂度

本演算法依旧用两层循现致玫举了很有子串，并针对所有子串都调用了一遍isUnique。但isUnique缓存了结果，所以实际上时间复杂度为$$\mathcal{O}(n^2)$$。

空间复杂度

cachedAnswers最多保存n个值，charSets最多保存所有子串，最多$$\sum _{i=1}^{n}n\times (n+1-i)$$。空间复杂度为：

$$\begin{array}{rl}{C}_{space}& =\mathcal{O}(n+\sum _{i=1}^{n}n\times (n+1-i))\\ & =\mathcal{O}(n^2)\end{array}$$

滑动窗口法

假设子串a由子串b和c组成，若b包含重复字符，则子串a也必包含重复字符。

将字符串所有子串以树的形式展现，以上论断可以描述为：

若很根到某内部节点之间的路径包含重复字符，则从根节点到以该内部节点为根的任意一个节点之间的路径都包含重复字符。

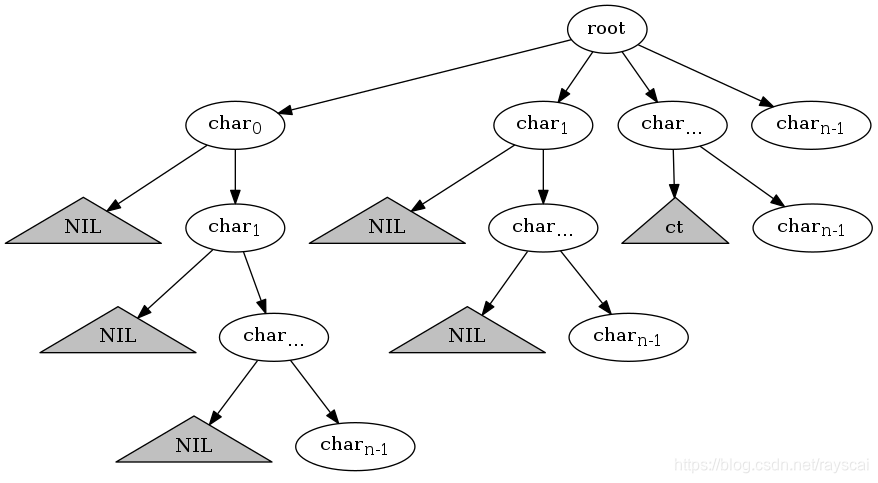
由此，我们可以快速排除掉不可能的子串。如下列代码所示，当发现重复字符，立即放弃对后续以相同字符为起始的子串的探索。

    int maxLength = 0;
    for (int start = 0; start < s.length(); start++) {
      for (int end = start + 1; end <= s.length(); end++) {
        if (isUnique.apply(start, end)) {
          maxLength = Math.max(maxLength, end - start);
        }else{
          continue;
        }
      }
    }
    return maxLength;

算法总结为：

• 已包含字符集合初始为空，滑动窗口初始为(0,0)
• 若窗口右端字符不在已包含字符集合中，则将窗口向右扩展一位
• 若窗口右端子符在已包含字符集合中，则将窗口左端向右收缩一位

上述「动态规划法」的空间复杂度也可以进一步优化。

代码实现

package io.github.rscai.leetcode.bytedance.string;

import java.util.HashSet;
import java.util.Set;

public class Solution1012C {

  public int lengthOfLongestSubstring(String s) {
    Set<Character> charSet = new HashSet<>();
    int maxLength = 0;
    int start = 0;
    int end = 0;
    while (start < s.length() && end < s.length()) {
      if (!charSet.contains(s.charAt(end))) {
        charSet.add(s.charAt(end));
        maxLength = Math.max(maxLength, end - start + 1);
        end++;
      } else {
        charSet.remove(s.charAt(start));
        start++;
      }
    }
    return maxLength;
  }
}

首先，初始化已包含字符集合为空，这?使用HashSet实现集合以达到常数复杂度检测集合是否包含字符。初始化滑动窗口为0到0，即仅包含第一个字符。

当窗口右端字符不在已包含字符集合中，则将其加入已包含字符集合，并将窗口右端向右扩展一位。同时检测当前子串是否长于最大无重复字符子串，是则更新最大无重复字符子串长度为当前子串长度。

当窗口右端字符在已包含字符集合中，则将窗口左端字符移出已包含字符集合，并将窗口左端向右收缩一位。

复杂度分析

时间复杂度

唯一的while循环中有两个索引start和end，最坏情况下，两个索引分别移动了$$n$$次。每次循环中价执行一次contains和add或remove。这?集合使用HashSet实现，HashSet的contains, add, remove都是常数复杂度运算。所以，总体时间复杂度为：

$$\begin{array}{rl}{C}_{time}& =\mathcal{O}(2n)\\ & =\mathcal{O}(n)\end{array}$$

空间复杂度

本演算法总共使用了四个变量charSet, maxLengthm start, end。其中，charSet只存储一个子串，而最大子串的长度为$$n$$。所以，空间复杂度为：

$$\begin{array}{rl}{C}_{space}& =\mathcal{O}(n+1+1+1)\\ & =\mathcal{O}(n)\end{array}$$