目录
stack专题:
32 Longest Valid Parentheses
给定一个只包含
'('和')'的字符串,找出最长的包含有效括号的子串的长度。示例 1:
输入: "(()" 输出: 2 解释: 最长有效括号子串为"()"示例 2:
输入: ")()())" 输出: 4 解释: 最长有效括号子串为"()()"
注意这题栈的使用技巧:
1.stack里面永远只有(,而没有 )。所以paranStack.pop()弹出的一定是(。
2.保存进stack里的并不是(,而是( 的下标,所以paranStack.top()的值是( 的下标。
基本思路:
遍历一遍数组
如果遇到左括号,把当前左括号的下标装进stack里面。
如果遇到右括号,则判断当前栈是否为空,如果为空,说明没有可以匹配的左括号,则跳过这个右括号,如果栈不为空,说明栈中还有左括号可以匹配,那么弹出一个左括号。弹出后如果栈为空。说明,从lastValidIndx开始就一直都是合法的括号匹配。那么maxLength=max(maxLength, indx-lastValidIndx+1);如果栈不为空,说明当前只是匹配成功了一部分,并不是从一开始就一直匹配成功,在中间有个左括号没有匹配到,那么对于此时的情况来说,maxLength等于这个被卡住的左括号之后的匹配成功的括号数。比如输入()((),此时lastValidIndx = 0,paranStack.top()为2.
class Solution {
public:
int longestValidParentheses(string s) {
stack<int> paranStack;
int maxLength=0;
int lastValidIndx=0;
for (int indx=0; indx<s.length(); indx++) {
if (s[indx]=='(') //遇到左括号,直接存入。
paranStack.push(indx);
else { //遇到右括号,分情况讨论
if (paranStack.empty()) //如果此时栈里左括号已经被消耗完了,没有额外的左括号用来配对当前的右括号了,那么当前的右括号就被单出来了,表明当前子串可以结束了,此时的右括号也成为了下一个group的分界点,此时右括号下标为index,所以下一个group的起始点为index+1,相当于skip掉当前的右括号。
lastValidIndx=indx+1;
else { //如果此时栈不空,可能有两种情况,1)栈正好剩下1个左括号和当前右括号配对 2)栈剩下不止1个左括号,
paranStack.pop();
if (paranStack.empty()) //栈pop()之前正好剩下1个左括号,pop()之后,栈空了,此时group长度为indx-lastValidIndx
maxLength=max(maxLength, indx-lastValidIndx+1);
else //栈有pop()之前剩下不止1个左括号,此时额外多出的左括号使得新的group形成。如()(()())中index=4时,stack中有2个左括号
maxLength=max(maxLength, indx-paranStack.top());
}
}
}
return maxLength;
}
};
技巧题:
31. Next Permutation
实现获取下一个排列的函数,算法需要将给定数字序列重新排列成字典序中下一个更大的排列。
如果不存在下一个更大的排列,则将数字重新排列成最小的排列(即升序排列)。
必须原地修改,只允许使用额外常数空间。
以下是一些例子,输入位于左侧列,其相应输出位于右侧列。
1,2,3→1,3,23,2,1→1,2,31,1,5→1,5,1
思路:从后向前扫描,碰到后一个数比前一个数更小,则记下这个数,并从这里向后扫描(或者从末尾往前扫描也行),寻找刚好比这个数大的数,即让头变得更大。 然后反转这个数之后的其他位置的数。让尾巴更小。

public class Solution {
public void nextPermutation(int[] nums) {
int i = nums.length - 2;
while (i >= 0 && nums[i + 1] <= nums[i]) {
i--;
}
if (i >= 0) {
int j = nums.length - 1;
while (j >= 0 && nums[j] <= nums[i]) {
j--;
}
swap(nums, i, j);
}
reverse(nums, i + 1);
}
private void reverse(int[] nums, int start) {
int i = start, j = nums.length - 1;
while (i < j) {
swap(nums, i, j);
i++;
j--;
}
}
private void swap(int[] nums, int i, int j) {
int temp = nums[i];
nums[i] = nums[j];
nums[j] = temp;
}
}桶排序:
41 First Missing Positive
给定一个未排序的整数数组,找出其中没有出现的最小的正整数。
示例 1:
输入: [1,2,0] 输出: 3示例 2:
输入: [3,4,-1,1] 输出: 2示例 3:
输入: [7,8,9,11,12] 输出: 1
思路:先把数值小于数组长度的数安排在i+1的位置上。然后剩下超出数组长度的值不要管。直接重新遍历一遍数组,找出没有安排在合适位置上的数,返回最先找到的数的下标
比如
【3,4,5,6】
第一个for循环后,3被安排在了下标3的位置
【6,4,5,3】
重新扫描一遍数组,发现6 != 1,所以返回1
class Solution
{
public:
int firstMissingPositive(int A[], int n)
{
for(int i = 0; i < n; ++ i)
while(A[i] > 0 && A[i] <= n && A[A[i] - 1] != A[i])
swap(A[i], A[A[i] - 1]);
for(int i = 0; i < n; ++ i)
if(A[i] != i + 1)
return i + 1;
return n + 1;
}
};贪心算法:
42.Trapping Rain Water
给定 n 个非负整数表示每个宽度为 1 的柱子的高度图,计算按此排列的柱子,下雨之后能接多少雨水。
上面是由数组 [0,1,0,2,1,0,1,3,2,1,2,1] 表示的高度图,在这种情况下,可以接 6 个单位的雨水(蓝色部分表示雨水)。 感谢 Marcos 贡献此图。
示例:
输入: [0,1,0,2,1,0,1,3,2,1,2,1] 输出: 6
这题可以归类为贪心
【分析】
1. 从左往右扫描一遍,对于每个柱子,求取左边最大值,保存进数组;
2. 从右往左扫描一遍,对于每个柱子,求最大右值,保存进数组;
3. 再扫描一遍,把每个柱子的面积并累加。
对于每个柱子,找到其左右两边最高的柱子,该柱子能容纳的面积就是 min(leftMostHeight[i],rightMostHeight[i]) - A[i];
class Solution {
public:
int trap(int A[], int n) {
if(A == NULL || n < 1)return 0;
int i;
int* leftMostHeight = (int*)malloc(sizeof(int)*n);
int* rightMostHeight = (int*)malloc(sizeof(int)*n);
int maxHeight = 0;
for(i = 0; i < n;i++){
leftMostHeight[i] = maxHeight;
if(maxHeight < A[i]){
maxHeight = A[i];
}
}
maxHeight = 0;
for(i = n-1;i >= 0;i--){
rightMostHeight[i] = maxHeight;
if(maxHeight < A[i]){
maxHeight = A[i];
}
}
int water = 0;
for(i =0; i < n; i++){
int curWater = min(leftMostHeight[i],rightMostHeight[i]) - A[i];
if(curWater > 0){
water += curWater;
}
}
return water;
}
};
45 Jump Game II
这题思路就是贪心算法,贪心原则是 在上一个最远距离的范围内找到下一跳的最远距离
比如【2,3,7,1,1,1,1】
第一跳在数字2的基础上往后跳,到7的位置,那么我现在要找下标是1-2这个范围内的下一跳最大能跳多远。
class Solution {
public:
int jump(int A[], int n) {
int ret = 0;//当前跳数
int last = 0;//上一跳可达最远距离
int cur = 0;//当前一跳可达最远距
for (int i = 0; i < n; ++i) {
//无法向前继跳直接返回
if(i>cur){ //有可能无论怎么跳,都不能到达终点或者越过终点,比如[3,2,1,0,4]。
return -1;
}
//需要进行下次跳跃,则更新last和当执行的跳数ret
if (i > last) {
last = cur;
++ret;
}
//记录当前可达的最远点
cur = max(cur, i+A[i]);
}
return ret;
}
};
回溯法专题:
回溯法框架:子集问题
78. Subsets
给定一组不含重复元素的整数数组 nums,返回该数组所有可能的子集(幂集)。
说明:解集不能包含重复的子集。
示例:
输入: nums = [1,2,3] 输出: [ [3], [1], [2], [1,2,3], [1,3], [2,3], [1,2], [] ]
public List<List<Integer>> subsets(int[] nums) {
List<List<Integer>> list = new ArrayList<>();
backtrack(list, new ArrayList<>(), nums, 0);
return list;
}
private void backtrack(List<List<Integer>> list , List<Integer> tempList, int [] nums, int start){
list.add(new ArrayList<>(tempList));
for(int i = start; i < nums.length; i++){
tempList.add(nums[i]);
backtrack(list, tempList, nums, i + 1);
tempList.remove(tempList.size() - 1);
}
}解法二:
public List<List<Integer>> subsets(int[] nums) {
List<List<Integer>> result = new ArrayList<>();
backtrack(result, new ArrayList<Integer>(), nums, 0);
return result;
}
void backtrack(List<List<Integer>> result, List<Integer> tempList, int[] nums, int start){
if(nums.length == start){
result.add(new ArrayList<>(tempList));
return;
}
tempList.add(nums[start]);
backtrack(result, tempList, nums, start+1);
tempList.remove(tempList.size()-1);
backtrack(result, tempList, nums, start+1);
}
90. Subsets II(去除重复子集)
利用排序思想去重
public List<List<Integer>> subsetsWithDup(int[] nums) {
List<List<Integer>> list = new ArrayList<>();
Arrays.sort(nums);
backtrack(list, new ArrayList<>(), nums, 0);
return list;
}
private void backtrack(List<List<Integer>> list, List<Integer> tempList, int [] nums, int start){
list.add(new ArrayList<>(tempList));
for(int i = start; i < nums.length; i++){
if(i > start && nums[i] == nums[i-1]) continue; // skip duplicates
tempList.add(nums[i]);
backtrack(list, tempList, nums, i + 1);
tempList.remove(tempList.size() - 1);
}
} 46. Permutations (全排列问题)
Given a collection of distinct integers, return all possible permutations.
Example:
Input: [1,2,3] Output: [ [1,2,3], [1,3,2], [2,1,3], [2,3,1], [3,1,2], [3,2,1] ]
错误解法:
class Solution {
public List<List<Integer>> permute(int[] nums) {
List<List<Integer>> list = new ArrayList<>();
backtrack(list, new ArrayList<>(), nums);
return list;
}
private void backtrack(List<List<Integer>> list, List<Integer> tempList, int [] nums){
if(tempList.size() == nums.length){
list.add(new ArrayList<>(tempList));
} else{
for(int i = 0; i < nums.length; i++){
tempList.add(nums[i]);
backtrack(list, tempList, nums);
tempList.remove(tempList.size() - 1);
}
}
}
}如果是这样写,则输出:
Input
[1,2,3]
Output
[[1,1,1],[1,1,2],[1,1,3],[1,2,1],[1,2,2],[1,2,3],[1,3,1],[1,3,2],[1,3,3],[2,1,1],[2,1,2],[2,1,3],[2,2,1],[2,2,2],[2,2,3],[2,3,1],[2,3,2],[2,3,3],[3,1,1],[3,1,2],[3,1,3],[3,2,1],[3,2,2],[3,2,3],[3,3,1],[3,3,2],[3,3,3]]
Expected
[[1,2,3],[1,3,2],[2,1,3],[2,3,1],[3,1,2],[3,2,1]]
-----
相当于打印了一个矩阵
[1, 2, 3]
1. 1 1
2. 2. 2
3. 3 3
如图:
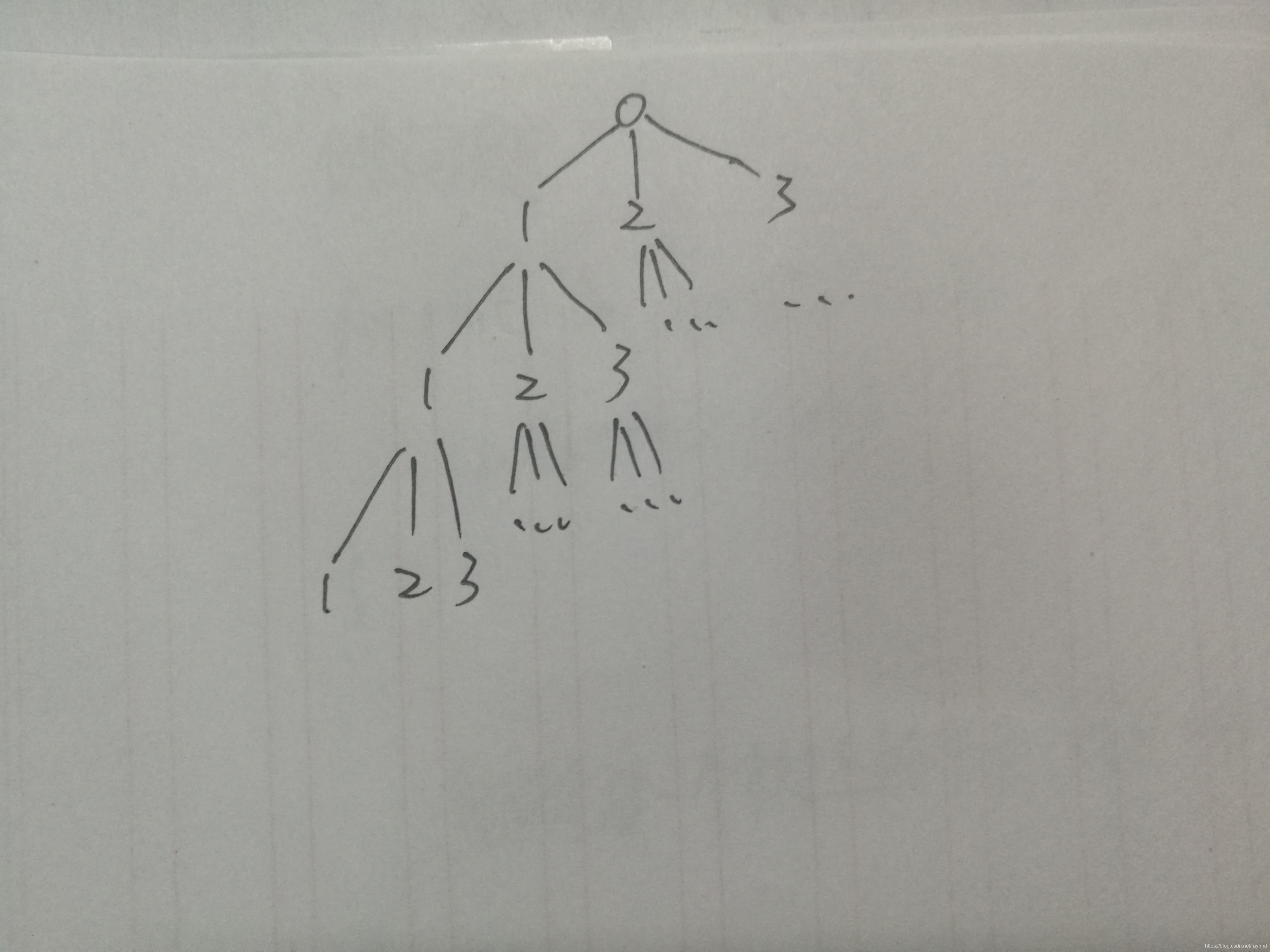
正确解法:
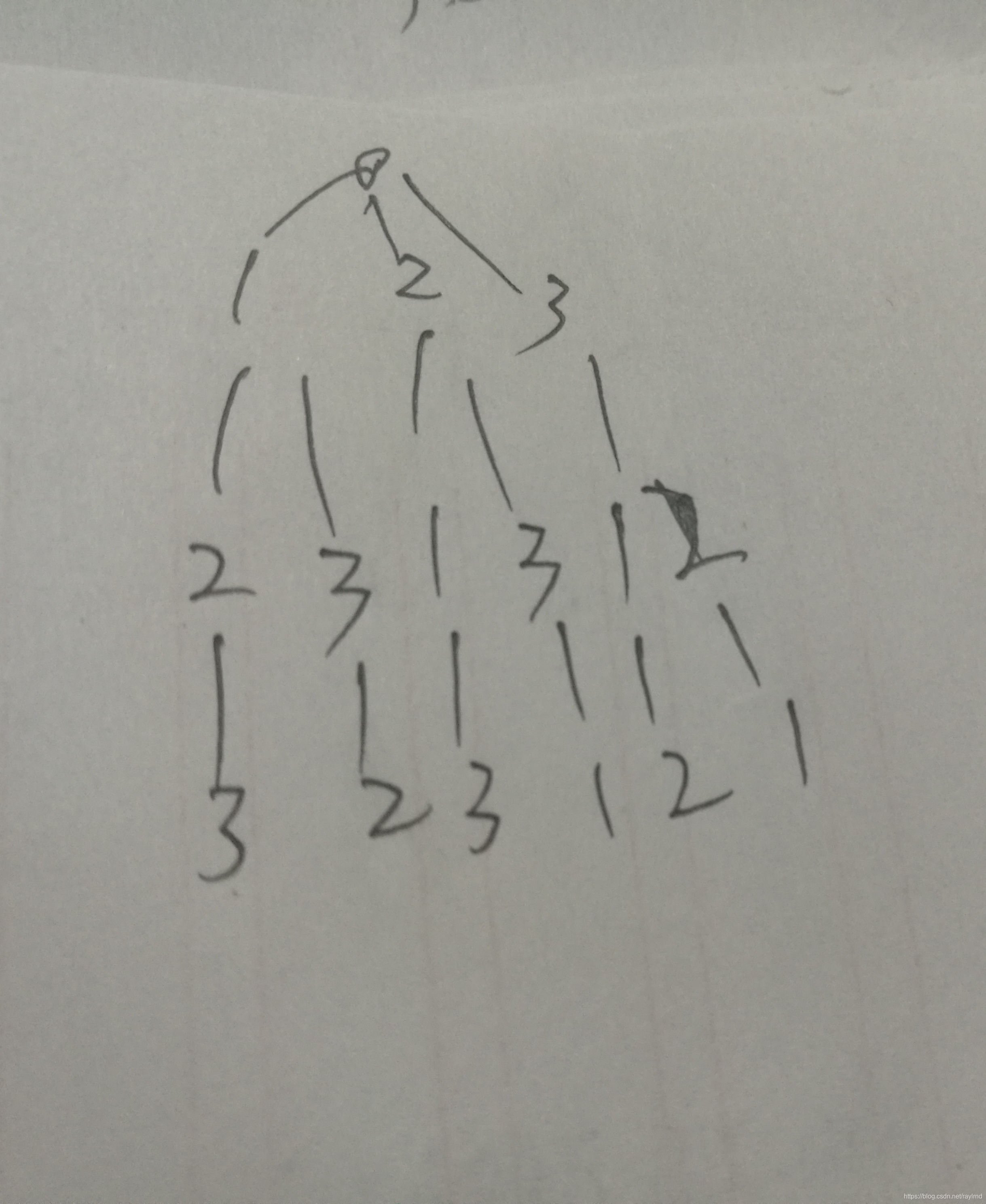
class Solution {
public List<List<Integer>> permute(int[] nums) {
List<List<Integer>> list = new ArrayList<>();
backtrack(list, new ArrayList<>(), nums);
return list;
}
private void backtrack(List<List<Integer>> list, List<Integer> tempList, int [] nums){
if(tempList.size() == nums.length){
list.add(new ArrayList<>(tempList));
} else{
for(int i = 0; i < nums.length; i++){
if(tempList.contains(nums[i])) continue; // element already exists, skip
tempList.add(nums[i]);
backtrack(list, tempList, nums);
tempList.remove(tempList.size() - 1);
}
}
}
}标准解法:
class Solution {
public:
vector<vector<int> > permute(vector<int> &num) {
vector<vector<int> > result;
permuteRecursive(num, 0, result);
return result;
}
void permuteRecursive(vector<int> &num, int begin, vector<vector<int>> &result) {
if (begin >= num.size()) {
result.push_back(num);
return;
}
for (int i = begin; i < num.size(); i++) {
swap(num[begin], num[i]);
permuteRecursive(num, begin + 1, result);
swap(num[begin], num[i]);
}
}
};40 Combination Sum II
给定一个数组
candidates和一个目标数target,找出candidates中所有可以使数字和为target的组合。
candidates中的每个数字在每个组合中只能使用一次。说明:
- 所有数字(包括目标数)都是正整数。
- 解集不能包含重复的组合。
示例 1:
输入: candidates =[10,1,2,7,6,1,5], target =8, 所求解集为: [ [1, 7], [1, 2, 5], [2, 6], [1, 1, 6] ]示例 2:
输入: candidates = [2,5,2,1,2], target = 5, 所求解集为: [ [1,2,2], [5] ]
这题是用的标准的回溯法子集数框架写的
比如:输入[1,2,3,4]
那么中间结果是:
1,2,3,4
1,3,4
1,4
2,3,4
2,4
3,4
4
列出了所有的组合情况,然后去筛选,满足条件的就保存起来。
class Solution {
public:
vector<vector<int> > combinationSum2(vector<int> &num, int target) {
sort(num.begin(), num.end());
vector<vector<int> > ret;
vector<int> cur;
Helper(ret, cur, num, target, 0);
return ret;
}
void Helper(vector<vector<int> > &ret, vector<int> cur, vector<int> &num, int target, int position)
{
if(target == 0)
ret.push_back(cur);
else
{
for(int i = position; i < num.size() && num[i] <= target; i ++)
{
if(i != position && num[i] == num[i-1])
continue;
cur.push_back(num[i]);
Helper(ret, cur, num, target-num[i], i+1);
cur.pop_back();
}
}
}
};这题的解法可以用在京东18笔试题上:
神奇数(京东2018校招C/C++工程师笔试大题第二道)
“
废话
上周末被学长远程抓壮丁答狗东2018的C++笔试题。2个小时4道大题,一个人做确实时间紧,记录一下学长甩给我第二题的神奇数。
想来自从6月份毕业就没再做过题,手生写的慢,好赖算是ac了,后来听说这题现场ac率10%我也是挺吃鲸的 =、=
闲话不多说,看题。
“
神奇数(京东2018校招C/C++工程师笔试大题第二道)
时间限制:1秒
空间限制:32768K
题目描述:
东东在一本古籍上看到有一种神奇数,如果能够将一个数的数字分成两组,其中一组数字的和等于另一组数字的和,我们就将这个数成为神奇数。例如242就是一个神奇数,我们能够将这个数的数字分成两组,分别是{2, 2}以及{4},而且这两组数的和都是4。东东现在需要统计给定区间内中有多少个神奇数,即给定区间(l, r),统计这个区间中有多少个神奇数,请你来帮助他。分析及解法
先把题目对神奇数的描述翻译成人话:“给你一个数,按位拆开后分成两堆儿,两堆儿的和相等”。我们把区间内的数字按位拆开可以得到一个n位的数组,然后求其组合:
CmnCnm (m = 1, 2, … n/2)
对组合结果求和,判断是否等于按位总和的一半。
这题用DP很难想出来,所以说不要在笔试的时候用DP,除非这题就是专门考你DP
#include <iostream>
#include <vector>
using namespace std;
int l=0,r=0;
//动态规划
bool canPartition(vector<int>&dicts,int n,int sum)
{
vector<vector<bool>> dp(n+1,vector<bool>(sum+1,false));
for(int i=0; i<=n; i++)
dp[i][0] = true;
for(int j=1; j<=sum; j++){
for(int i=1; i<=n; i++){
dp[i][j] = dp[i-1][j]; //不选第i个元素
if(j>=dicts[i-1]) //选第i个元素
dp[i][j] = dp[i][j] || dp[i-1][j-dicts[i-1]];
}
}
return dp[n][sum];
}
bool isSqs(int num)
{
vector<int> dicts(10,0);
int k=0,sum=0;
while(num!=0){
dicts[k++] = num%10;
num /= 10;
sum += dicts[k-1];
}
if(sum & 1)
return false;
return canPartition(dicts,k,sum>>1);
}
int sqs()
{
if(r<11)
return 0;
if(r==11)
return 1;
int cnt = 1;
for(int i=12; i<=r; i++){
if(isSqs(i))
cnt++;
}
return cnt;
}
int main()
{
cin>>l>>r;
cout<<sqs();
return 0;
}这题回溯法跟上一题有所不同
bool res1 = isfind( nums, sum, cur+nums[begin], begin+1 );
bool res2 = isfind( nums, sum, cur, begin+1 );
这两个递归式表达了一个数取还是不取两种情况,联想一下二叉树的左右分支。
bool isfind(vector<int>& nums, int sum, int cur, int begin)
{
if( begin == nums.size() ) return false;
if( cur == sum / 2 ) return true;
bool res1 = isfind( nums, sum, cur+nums[begin], begin+1 );
if( res1 ) return true;
bool res2 = isfind( nums, sum, cur, begin+1 );
if( res2 ) return true;
return res1 || res2;
}
当然也可以用回溯法框架做。
验证该数是否是神奇数
bool func(int *a,int l,int size,int num,int sum)
{
bool ans=false;
for(int i=l; i<r; i++)
{
if((num+a[i])*2<=sum)
{
if((num+a[i])*2==sum) return true;
else ans = ans || func(a,i+1,size,num+a[i],sum);
}
}
return ans;
}bool fenjie(long long n)
{
vector<int> dig;
int sum = 0;
if(n==0)
{
dig.push_back(0);
return false;
}
int t =0;
while(n>0)
{
t = n%10;
n/=10;
dig.push_back(t);
sum+=t;
}
sort(dig.begin(),dig.end());
if(sum&1)return false;
return isfind(dig,sum,0,0);
}
void core()
{
int n,m,ret =0;
cin>>n>>m;
for( int i = n; i <= m; i++ )
{
if (fenjie(i))ret++;
}
cout<<ret<<endl;
}
int main()
{
core();
}
#include <bits/stdc++.h>
using namespace std;
//这里实现了统计这个数有多少种组合方式。
int func(int *a,int l,int size,int num,int sum)
{
int ans=0;
for(int i=l; i<r; i++)
{
if((num+a[i])*2<=sum)
{
if((num+a[i])*2==sum) return 1;
else ans+=func(a,i+1,size,num+a[i],sum);
}
}
return ans;
}
/*
bool func(int *a,int l,int size,int num,int sum)
{
bool ans=false;
for(int i=l; i<r; i++)
{
if((num+a[i])*2<=sum)
{
if((num+a[i])*2==sum) return true;
else ans = ans || func(a,i+1,size,num+a[i],sum);
}
}
return ans;
}
*/
int main()
{
int ans=0,l,r;
scanf("%d%d",&l,&r);
for(int i=l; i<=r; i++)
{
int sum=0,now=i,a[10],count=0;
while(now)
{
sum+=now%10;
a[count++]=now%10;
now/=10;
}
if(sum&1) continue;
if(func(a,0,count,0,sum)) ans++;
}
printf("%d\n",ans);
return 0;
}
来看一道相似解法的回溯问题:
494. Target Sum
Root
/ \
+1 -1
/\ /\
+2 -2 +2 -2
/\ /\ /\ /\
+3 -3 ... +3 -3class Solution {
public:
int result;
int findTargetSumWays(vector<int>& nums, int S) {
rec(0, 0, nums, S);
return result;
}
void rec(int sum, int count, vector<int>& nums, int S) {
if(count == nums.size()) {
if(sum == S)
result++;
return ;
}
rec(sum + nums[count], count + 1, nums, S);
rec(sum - nums[count], count + 1, nums, S);
}
};
带备忘录的版本:
public class Solution {
public int findTargetSumWays(int[] nums, int S) {
if (nums == null || nums.length == 0){
return 0;
}
return helper(nums, 0, 0, S, new HashMap<>());
}
private int helper(int[] nums, int index, int sum, int S, Map<String, Integer> map){
String encodeString = index + "->" + sum;
if (map.containsKey(encodeString)){
return map.get(encodeString);
}
if (index == nums.length){
if (sum == S){
return 1;
}else {
return 0;
}
}
int curNum = nums[index];
int add = helper(nums, index + 1, sum - curNum, S, map);
int minus = helper(nums, index + 1, sum + curNum, S, map);
map.put(encodeString, add + minus);
return add + minus;
}
}路径问题(DFS,BFS,并查集)
130. Surrounded Regions
给定一个二维的矩阵,包含
'X'和'O'(字母 O)。找到所有被
'X'围绕的区域,并将这些区域里所有的'O'用'X'填充。示例:
X X X X X O O X X X O X X O X X运行你的函数后,矩阵变为:
X X X X X X X X X X X X X O X X解释:
被围绕的区间不会存在于边界上,换句话说,任何边界上的
'O'都不会被填充为'X'。 任何不在边界上,或不与边界上的'O'相连的'O'最终都会被填充为'X'。如果两个元素在水平或垂直方向相邻,则称它们是“相连”的。
用DFS做:
先把最外面的一圈元素遍历一遍,查找是否有连通的‘O’的路径,如果有,则全部变为‘1’。然后再整体遍历数组,将剩下的‘O’变为‘X’,把‘1’变为‘O’。
void solve(char **board, int rowSize, int colSize)
{
int row, col;
if (!board || !rowSize || !colSize)
return;
for (row = 0; row < rowSize; row++) {
check(board, row, 0, rowSize, colSize);
check(board, row, colSize - 1, rowSize, colSize);
}
for (col = 1; col + 1 < colSize; ++col) {
check(board, 0, col, rowSize, colSize);
check(board, rowSize - 1, col, rowSize, colSize);
}
for (row = 0; row < rowSize; ++row)
for (col = 0; col < colSize; ++col)
board[row][col] = board[row][col] == '1' ? 'O' : 'X';
}
void check(char **board, int row, int col, int rowSize, int colSize)
{
if (row < 0 || col < 0 || row >= rowSize || col >= colSize || board[row][col] != 'O')
return;
board[row][col] = '1';
check(board, row, col - 1, rowSize, colSize);
check(board, row, col + 1, rowSize, colSize);
check(board, row + 1, col, rowSize, colSize);
check(board, row - 1, col, rowSize, colSize);
}BFS版本:
跟上面的不同是每个边界点按广度优先遍历
void bfs(int i, int j, vector<vector<char>> &board) {
int m = board.size();
int n = board[0].size();
queue<pair<int, int> > q;
q.push(make_pair(i, j));
while (!q.empty()) {
pair<int, int> elem = q.front();
q.pop();
i = elem.first;
j = elem.second;
if (i >= 0 && i < m && j >=0 && j < n && board[i][j] == 'O') {
board[i][j] = '#';
q.push(make_pair(i - 1, j));
q.push(make_pair(i + 1, j));
q.push(make_pair(i, j - 1));
q.push(make_pair(i, j + 1));
}
}
}用并查集做(C 语言版):
#define MAXN 100005
typedef struct DisjointSet{
int par,rank;
}DS;
DS ds[MAXN];
int dir[4][2] = {{1,0},{-1,0},{0,1},{0,-1}};
void init(int n)
{
for(int i = 0;i <= n;i++){
ds[i].par = i;
ds[i].rank = 0;
}
}
int find(int x)
{
if(x == ds[x].par)
return x;
else return ds[x].par = find(ds[x].par);
}
void unite(int x, int y)
{
x = find(x);
y = find(y);
if(x == y) return ;
if(ds[x].rank < ds[y].rank)
ds[x].par = y;
else if(ds[x].rank == ds[y].rank){
ds[y].rank++;
ds[x].par = y;
}else{
ds[y].par = x;
}
return ;
}
int same(int x, int y)
{
return find(x) == find(y);
}
void solve(char** board, int boardRowSize, int boardColSize) {
int brs = boardRowSize;
int bcs = boardColSize;
init(bcs * brs);
for(int i = 0;i < brs;i++){
for(int j = 0;j < bcs;j++){
if((i == 0 || i == brs-1 || j == 0 || j == bcs-1) && board[i][j] == 'O')
unite(i*brs+j, brs*bcs);
else if(board[i][j] == 'O'){
for(int k = 0;k < 4;k++){
int x = i + dir[k][0];
int y = j + dir[k][1];
if(board[x][y] == 'O')
unite(i*brs+j, x*brs+y);
}
}
}
}
for(int i = 0;i < brs;i++){
for(int j = 0;j < bcs;j++){
if(!same(i*brs+j, brs*bcs)) board[i][j] = 'X';
}
}
return ;
}单调栈和单调队列
单调队列用于找区间的最值问题,还可用于优化DP算法,如果DP表达式里有min{区间}或max{区间}这样的式子。
单调栈用于找第i个数左/右边第一个比他大的元素。
比如:
239. Sliding Window Maximum
就是用单调队列做
当扫描到一个元素的时候,就进入了一个循环,每个循环都要维护队列的性质
即维护
1. 队列中最多只能有三个元素
2. 把比第i个元素小的pop出队列
//双向单调队列
class Solution {
public:
vector<int> maxSlidingWindow(vector<int>& nums, int k) {
//双向队列是从大到小的 单调队列
vector<int> res;
deque<int> Q;
for(int i=0; i<nums.size(); i++){
if(!Q.empty() && Q.front() == i-k) Q.pop_front(); //队列中队首元素到当前的位置差是不是大于K,
while (!Q.empty() && nums[Q.back()] < nums[i]) {
Q.pop_back();
}
Q.push_back(i);
if(i >= k-1) res.push_back(nums[Q.front()]);
}
return res;
}
};比如:
42.Trapping Rain Water
可用单调栈做





 本文深入解析了多种经典算法问题,包括括号匹配、下一个排列、桶排序、贪心算法、回溯法、路径问题以及单调栈和单调队列的应用。通过具体示例,详细介绍了每种算法的实现思路和代码实现。
本文深入解析了多种经典算法问题,包括括号匹配、下一个排列、桶排序、贪心算法、回溯法、路径问题以及单调栈和单调队列的应用。通过具体示例,详细介绍了每种算法的实现思路和代码实现。

















 1万+
1万+

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








