本篇文章是博主在学习计算机组成原理后总结的一些知识点,文章中有误或者讲的不太明白请见谅,留言评论,博主看到后查询资料核实后会修改的。
目录
目录
一、数制与编码
1.进位计数法和各常见进制
(1)进位计数法
若一个r进制数(![]() )主要公式如下:
)主要公式如下:
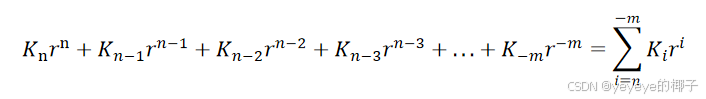
其中r为基数,是第i位的位权,
![]() 的值可以是0或者1。
的值可以是0或者1。
二进制是基数为2的计数制,其中只有0或者1两种。切记里面没有2!同样的8进制里面没有8也是一样的。
2.各进制的互相转换
(1)二进制转八进制数或者十六进制
二进制数转八或者十六进制数还是比较简单的。把一串二进制数分成3位(八进制)或者4位(十六进制),如果位数不够则需要在最左边补0即可。然后根据基数和位权相乘就可以得到对应的进制了,列如二进制数 111001010的转换:

(2)八进制或十六进制转二进制
同样的八进制或者十六进制可以转化为特定的二进制,过程就是二进制转八进制数或者十六进制的逆过程。
(3)任意进制转十进制
任意进制可以根据他们的权值和各位码数相乘,再把乘积相加即可。列如二进制11011运算如下:
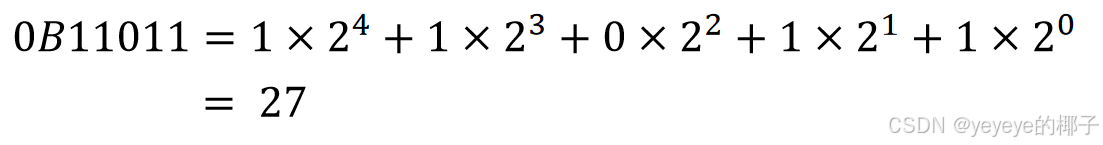
(4)十进制转任意进制
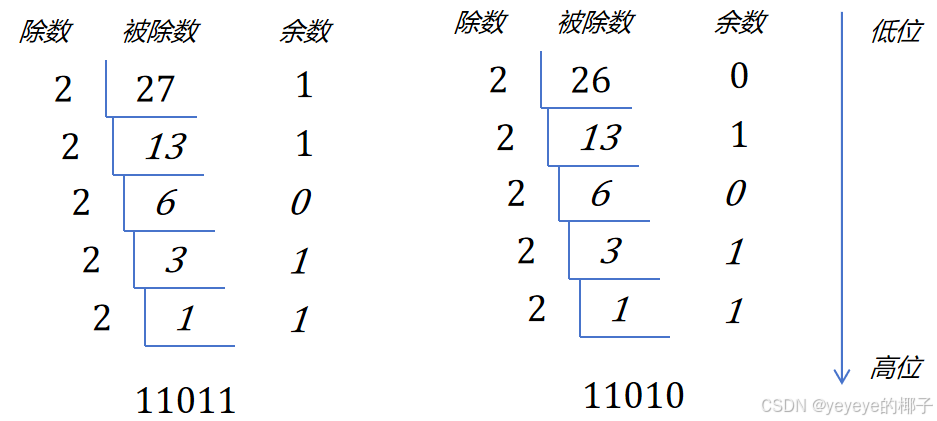
根据十进制来对其他进制进行转换,一般采取除基取余法,整数部分除基取余,最先取得的余数为最低位,最后取得的余数为最高位(即除基取余,先余为低,后余为高),列如:
3.真值和机器数
在日常生活中,通常使用正号、负号来分别正数和负数,列如:“+1”、“-4”。真值一般所代表的是机器数的实际值
在计算机中,一般将数的符号和数值部分一起编码,将符号数字化。通常用“0”代表“正”,用“1”代表“负”,这种将符号数字化的数被称为机器数。常用的由原码、补码、反码等。
4.无符号整数
一个编码的全部二进制均为数值为而没有符号位时,改编就是无符号整数。
5.定点整数和定点小数
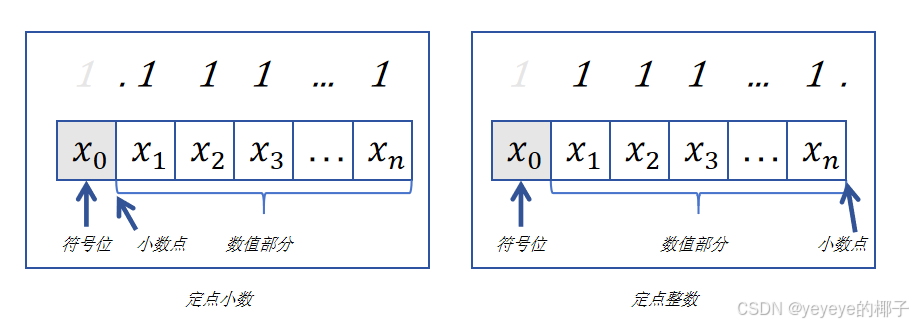
定点整数是计算机中表示整数的数值类型,其小数点固定在数值的最低位之后(实际上不显式表示小数点),仅用于存储整数部分。数值范围和精度受计算机字长限制。其中拓展位从左边开始。
定点小数则是计算机中表示小数的数值类型,小数点位置固定且隐含在数值中,能够表示纯小数。同样,其数值范围和精度也受计算机字长限制。其中拓展位从右边开始。
6.原码、补码、反码、移码
(这边仅作简单介绍)后面部分有总结
(1)原码表示法
用机器数的最高位表示数的符号位,其余各位表示数的绝对值,列如:
二进制:
=-1110,
=+1110
原码 :
=1,0001110,
=0,0001110 (字长为8位)
其中原码表示法有两个0分别是正0和负0
(2)反码表示法
反码表示对正负数有不同的处理方法,正数的反码就是正数本身,负数的反码处理为符号位不变,数值部分取反。
二进制:
=-1110,
=+1110
原码 :
=1,0001110,
=0,0001110 (字长为8位)
反码 :
=1,1110001,
=0,0001110 (字长为8位)
(3)补码表示法
补码表示对正负数有不同的处理方法,正数的补码就是正数本身,负数的补码处理为符号位不变,数值部分取反,最后再加上1。
二进制:
=-1110,
=+1110
原码 :
=1,0001110,
=0,0001110 (字长为8位)
反码 :
=1,1110001,
=0,0001110 (字长为8位)
补码 :
=1,1110010,
=0,0001110 (字长为8位)
(4)移码表示法
移码常用于表示浮点数的阶码部分,他只能表示整数
移码是在补码的基础上再将符号位取反。移码的最大特点是保持了数据原有的大小顺序,移码大真值就越大,移码小真值就越小。
二进制:
=-1110,
=+1110
原码 :
=1,0001110,
=0,0001110 (字长为8位)
反码 :
=1,1110001,
=0,0001110 (字长为8位)
补码 :
=1,1110010,
=0,0001110 (字长为8位)
移码 :
=0,1110010,
=1,0001110 (字长为8位)
(5)原码、反码、补码、移码总结
1)各码之间的转换
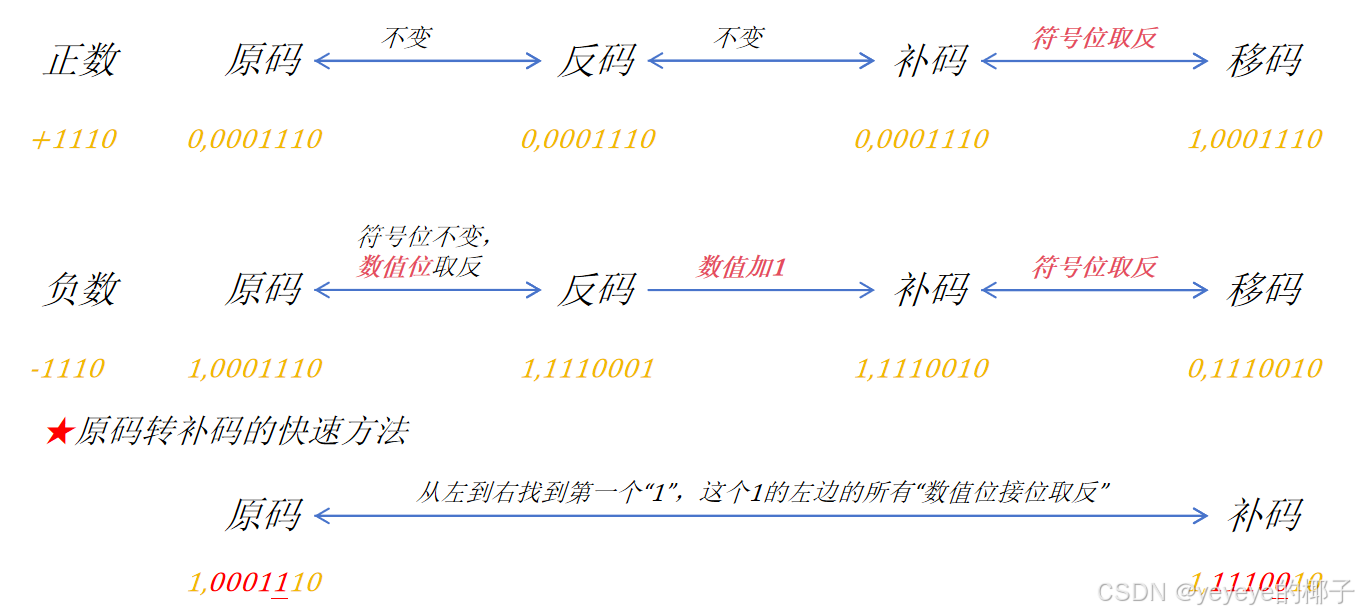
2)各码之间的特性
| n+1bit | 合法表示范围 | 最大的数 | 最小的数 | 真值0的表示 |
| 带符号整数:原码 | | [+0]=0,000...000 [-0]=1,000...000 | ||
| 带符号整数:反码 | [+0]=0,000...000 [ -0] =1,111...111 | |||
| 带符号整数:补码 | [0]=0,000...000 真值0只有一种补码 | |||
| 带符号整数:移码 | [0]=0,000...000 真值0只有一种移码 | |||
| 无符号整数 | 0000...000 |
原码和补码的合法表示范围完全相同,都有两种表示真值0,补码的合法表示范围比原码多一个页数,只有一种方法表示真值0。
若在8bit中,补码最小值为-128,原码反码最小值为-127。列如:(-64)+(-64)在原码中会溢出,但是在补码中不会。
| 行数 | 机器数 | 无符号数 | 原码 | 反码 | 补码 | 移码 |
| 1 | 0000 0000 | 0 | +0 | +0 | +0、-0 | -128 |
| 2 | 0000 0001 | 1 | +1 | +1 | +1 | -127 |
| 3 | 0000 0010 | 2 | +2 | +2 | +2 | -126 |
| ... | ... | ... | ... | ... | ... | ... |
| 126 | 0111 1101 | 125 | +125 | +125 | +125 | -3 |
| 127 | 0111 1110 | 126 | +126 | +126 | +126 | -2 |
| 128 | 0111 1111 | 127 | +127 | +127 | +127 | -1 |
| 129 | 1000 0000 | 128 | -0 | -127 | -128 | 0 |
| 130 | 1000 0001 | 129 | -1 | -126 | -127 | 1 |
| 131 | 1000 0010 | 130 | -2 | -125 | -126 | 2 |
| ... | ... | ... | ... | ... | ... | ... |
| 253 | 1111 1100 | 252 | -124 | -3 | -4 | 124 |
| 254 | 1111 1101 | 253 | -125 | -2 | -3 | 125 |
| 255 | 1111 1110 | 254 | -126 | -1 | -2 | 126 |
| 256 | 1111 1111 | 255 | -127 | -0 | -1 | 127 |
二、运算方法和运算电路
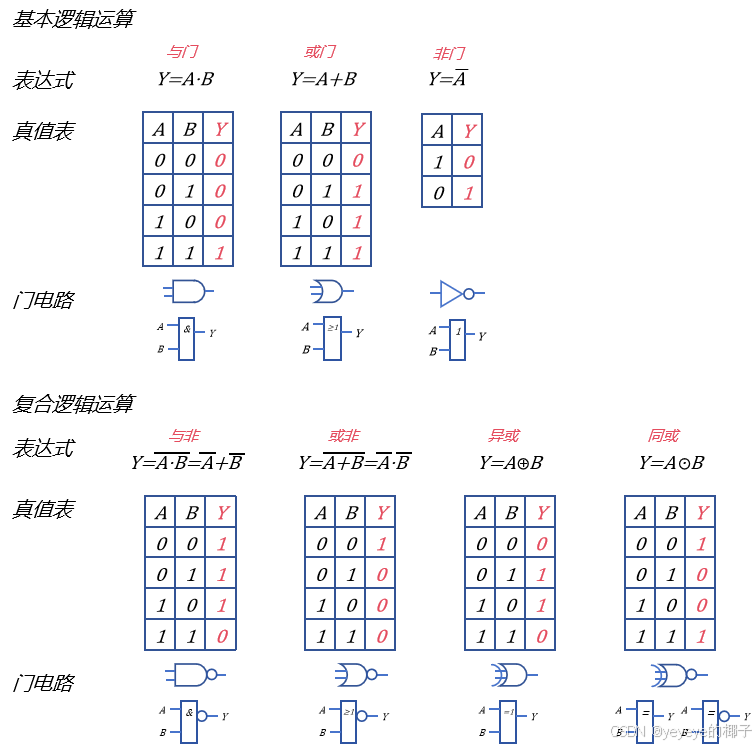
1.逻辑运算符
2.溢出的判别方法
补码定点数加减运算溢出判断的方法有3种
(1)采用1位符号位,对其进行计算。其中满足参加两个操作的数值的符号位相同,而计算结果的数值符号位产生了变化,则说明溢出。
(2)采用双符号位,也称为模4补码,在用于表示符号的符号位从1位变成2位。
类如:
其中有
:表示结果为正数,无溢出。
:表示结果正溢出。
:表示结果负溢出。
:表示结果为负数,无溢出。
(3)采用一位符号位根据数值位的进位情况进行判断溢出
若符号位(最高位)的进位
与最高数位(次高位)的进位
相同,说明无溢出,否则说明有溢出。相当于
与
的异或,如果结果为1(说明不相同),则溢出,否则不溢出。
3.标志符
| 符号名称 | 英文表示 | 意义 |
| 零标志 | ZF [Zero Flag] | 表示运算结果是否为0。 ZF=0表示运算结果为非零,ZF=1表示运算结果为0。 |
| 溢出标志 | OF [Overflow] | 判断有符号数是否溢出。如果时无符号整数的话,OF标志位无意义 OF=0表示没有溢出,OF=1表示溢出。 |
| 符号标志 | SF [Sign Flag] | 表示结果的符号。如果时无符号整数的话,OF标志位无意义 SF=0表示为正数或0,SF=1表示为负数 |
| 进/借位标志 | CF [Carry Flag] | 表示无符号整数运算时是否进行进位/借位 CF=0表示有进/借位,CF=1表示没有进/借位 |
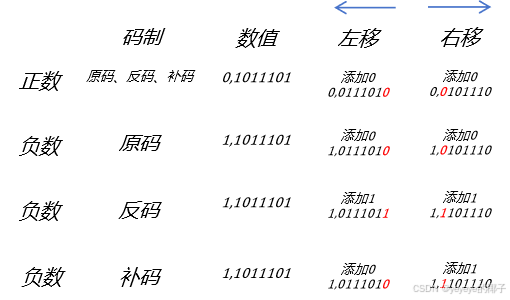
4.定点数的移位计算
(1)逻辑移位
逻辑移位将操作数视为无符号整数。逻辑移位规则:左移时,高位移除,低位补0;右移时,低位移除,高位补0。对于无符号整数逻辑左移,若高位的1移出,则发生溢出。
(2)算数移位
算数移位需要考虑符号位的问题,操作数位有符号整数
计算机中有符号整数一般使用补码表示的,因此对于符号位的移位操作应该采用补码算术移位的方式。算数移位的规则:左移时,高位移出,低位补0,若移除的高位不同于移位后的符号位,则发生溢出;右移时,低位移除,高位补符号位,若低位的1移出,影响精度。
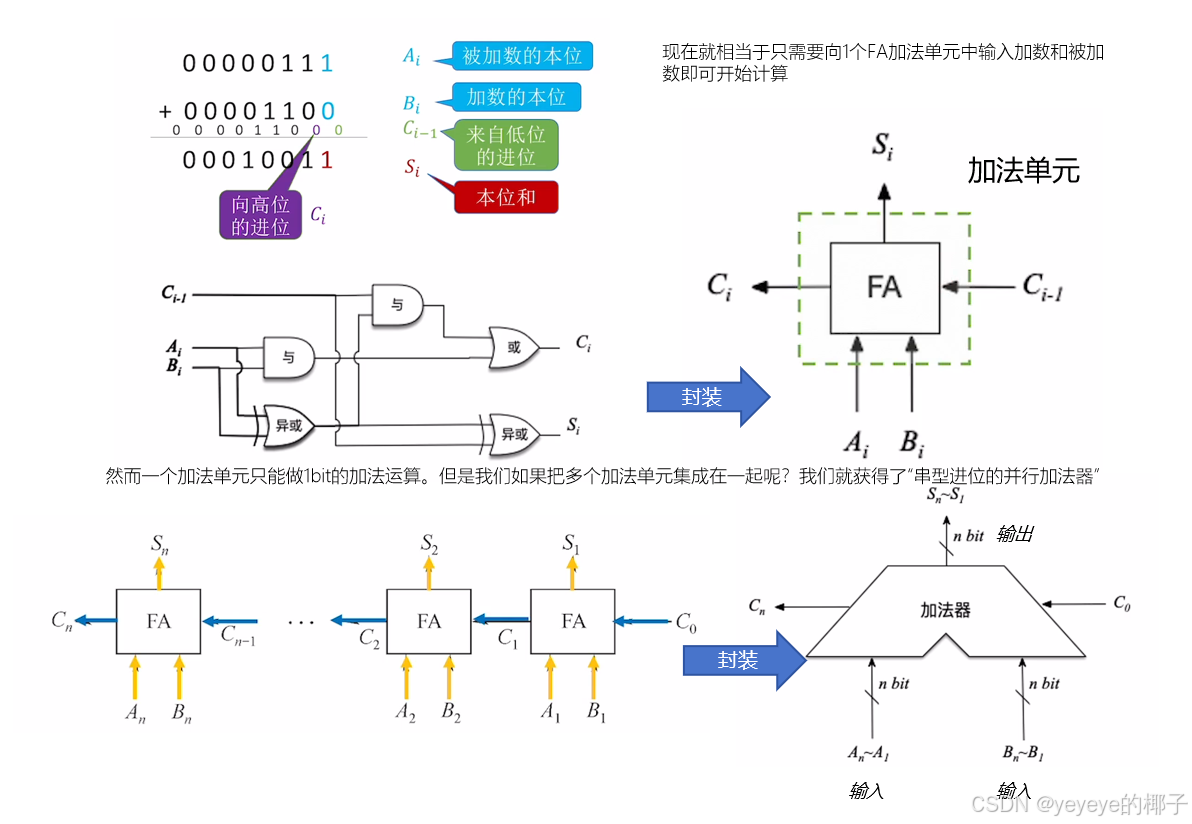
5.加法和减法手算模拟
(1)加法器的内部构造
众所周知,在算数逻辑单元(ALU)中核心为加法器,加法器中想要实现的功能必然是输入两个数,输出相加的结果。主要过程看下述图
(2)原码的加减法运算
该方法其实和我们日常做加减运算是一样的,但是在加法器中,如果还需要识别该数为正数还是负数,并且还要根据不同的情况来确定符号位的值,这是不实际的,所以在加法器中做加法运算还是使用补码来实现的。

如果采用下述规则中原码计算方法则不会出错
| 情况 | 应对方法 |
| 正+正 | 绝对值做加法,结果为正 【可能溢出】 |
| 负+负 | 绝对值做加法,结果为负 【可能溢出】 |
| 正+负 | 绝对值大的减绝对值小的,符号同绝对值大的数 |
| 负+正 | 绝对值大的减绝对值小的,符号同绝对值大的数 |

(3)补码的加减法运算
直接只有两个步骤:
①转补码
②按位相加
下面是一个例子:
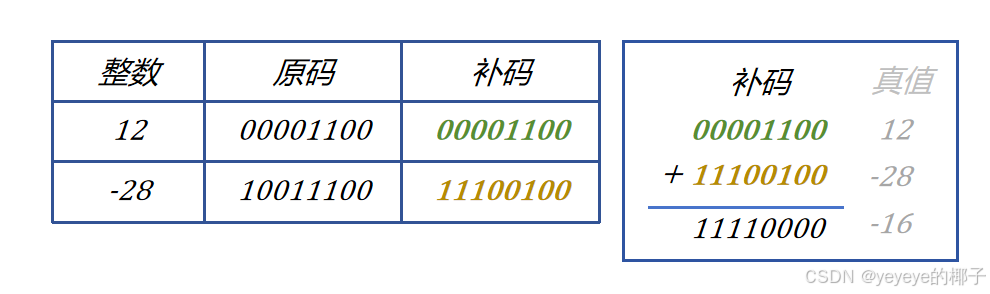
(4)无符号数加减法

6.乘法手算模拟
(1)原码的乘法手算模拟
原码的手算模拟步骤:ACC用于放高位的结果,MQ用于放低位部分积/乘数
①由乘数的最低位来判断,如果是1则让通用寄存器表示位+,即加上被乘数。如果是0,则就加上一串0就好。
②加法完毕后,需要把高位部分积和低位部分积的部分向右移1位,右移移除的位为丢弃位(移除的部分是刚刚代表通用寄存器的部分,已经乘过了,失去意义了,丢弃了也没有关系)右移符号位不动,补0即可。
③重复①②两个步骤即可,直到所有的乘数被丢弃。最后高位部分积和低位部分积的拼接在一起,就是相乘后的结果。
④根据乘数和被乘数的符号位异或的结果,就是乘数后的符号位的值。
(即1和1为0,1和0为1,0和0为0)
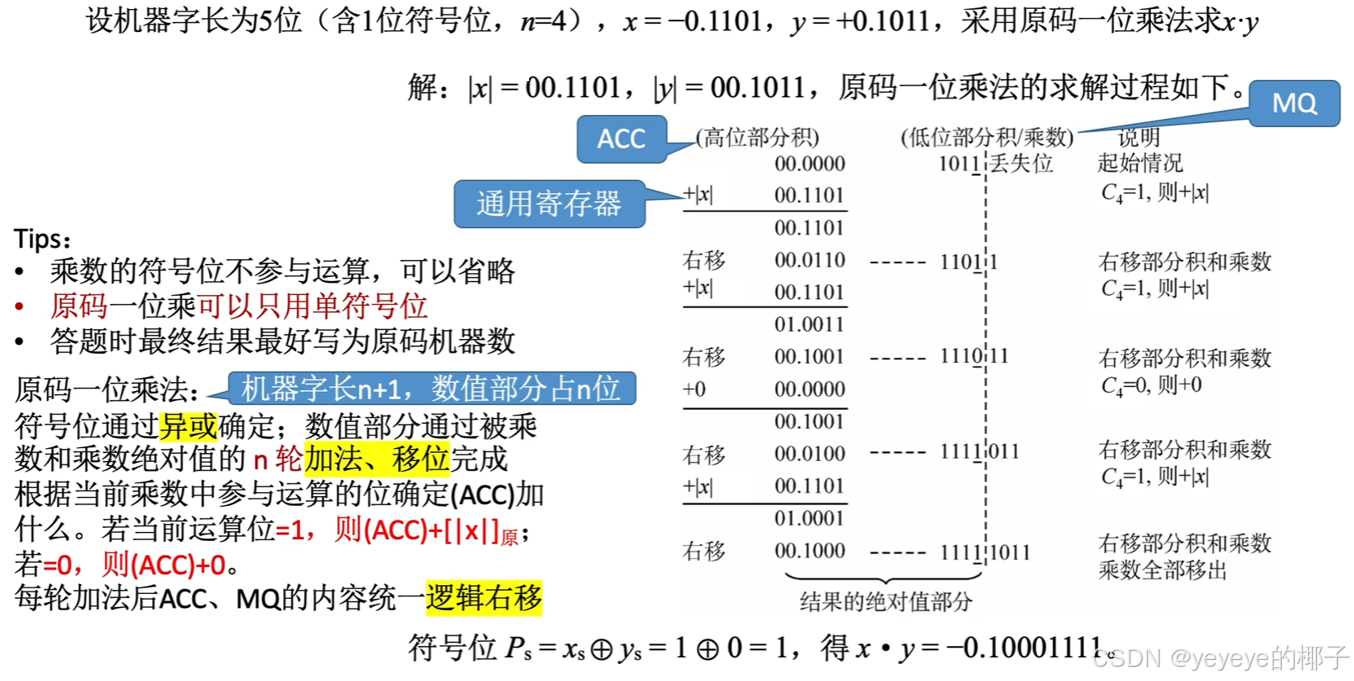
(2)补码的手算模拟
原码的手算模拟步骤:ACC用于放高位的结果,MQ用于放低位部分积/乘数
①通过辅助位-MQ中最低位的情况不同,根据加法规则来进行不同的反应,加法规则下图中有。
②加法完毕后,需要把高位部分积和低位部分积的部分向右移位,右移移除的位为丢弃位(移除的部分是刚刚代表通用寄存器的部分,已经乘过了,失去意义了,丢弃了也没有关系)右移符号位不动,补符号的数值即可。
③重复①②两个步骤即可,直到所有的乘数被丢弃(其中不包括符号位)。最后高位部分积和低位部分积的拼接在一起,就是相乘后的结果。
④将最后结果(高位部分积和低位部分积拼接起来)经过补码转原码即可。

7.除法手算模拟
(1)原码除法:恢复余数法与加减交替法
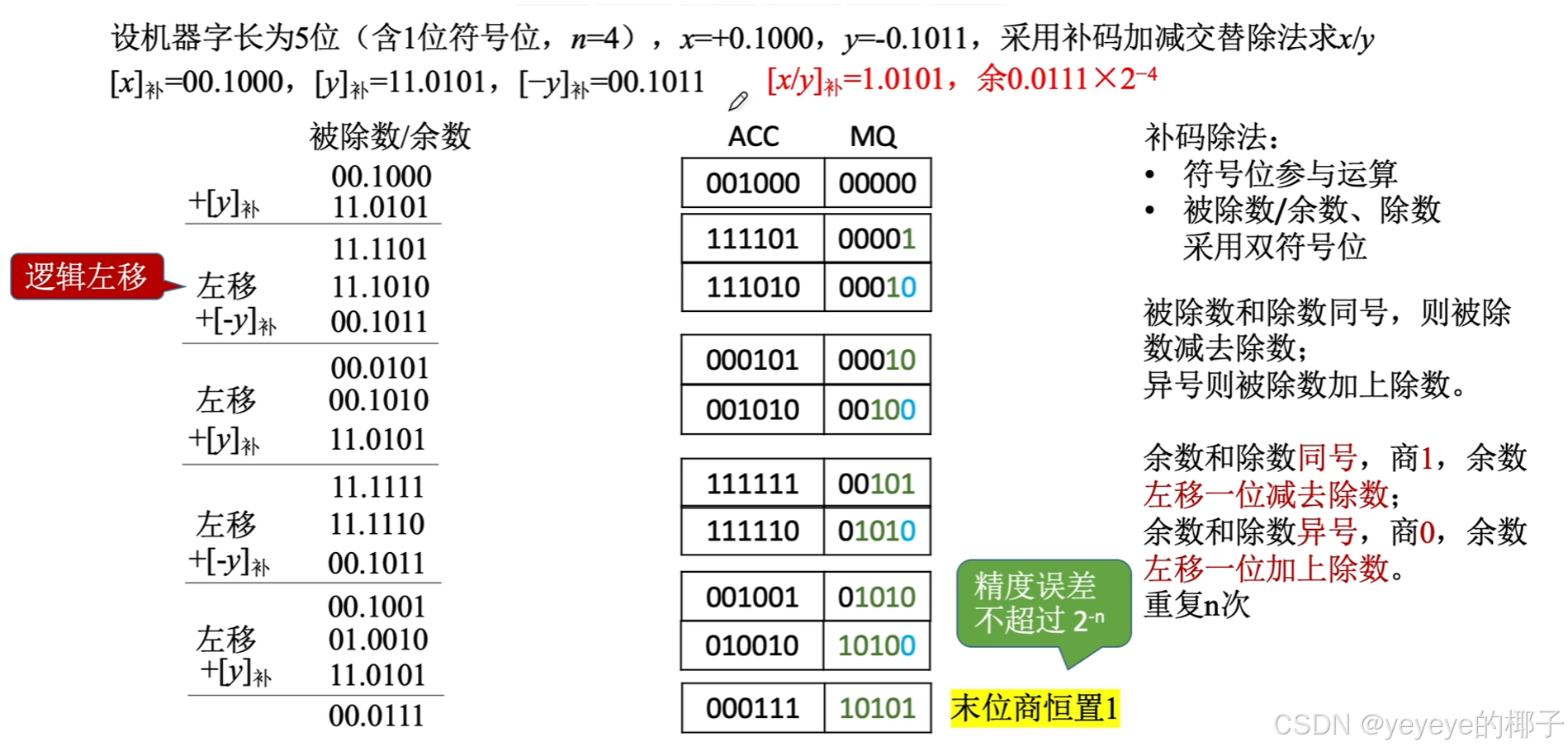
恢复余数法:是先对被除数,先尝试减一下,如果结果为负数,则商0,把之前尝试的减还原一下;如果为正数,则商1。符号位还是和乘法一样采用异或运算。
加减交替法:这个方法和恢复余数法的区别在于简化了新余数判正负后面的处理使得原先需要恢复后再做处理,变得一步到位了。符号位还是和乘法一样采用异或运算。流程图如下:
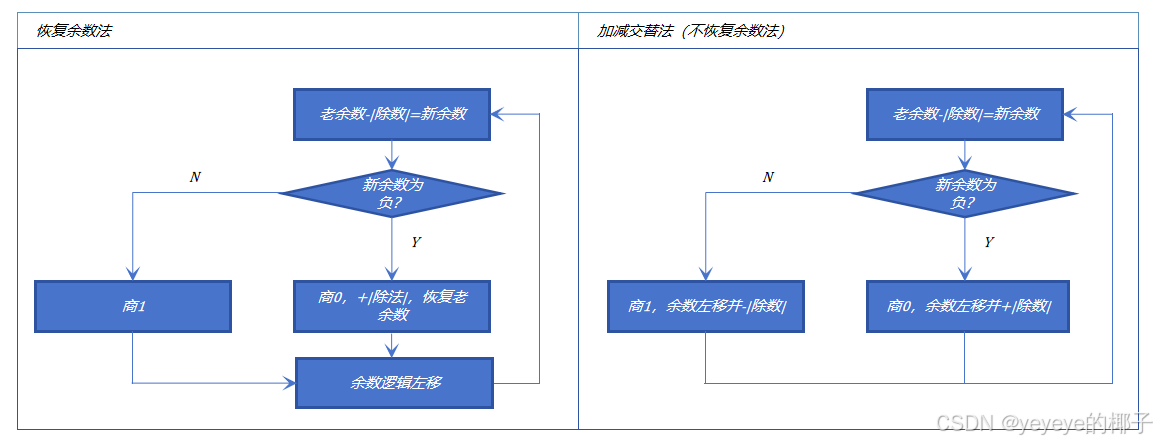
例题对比:
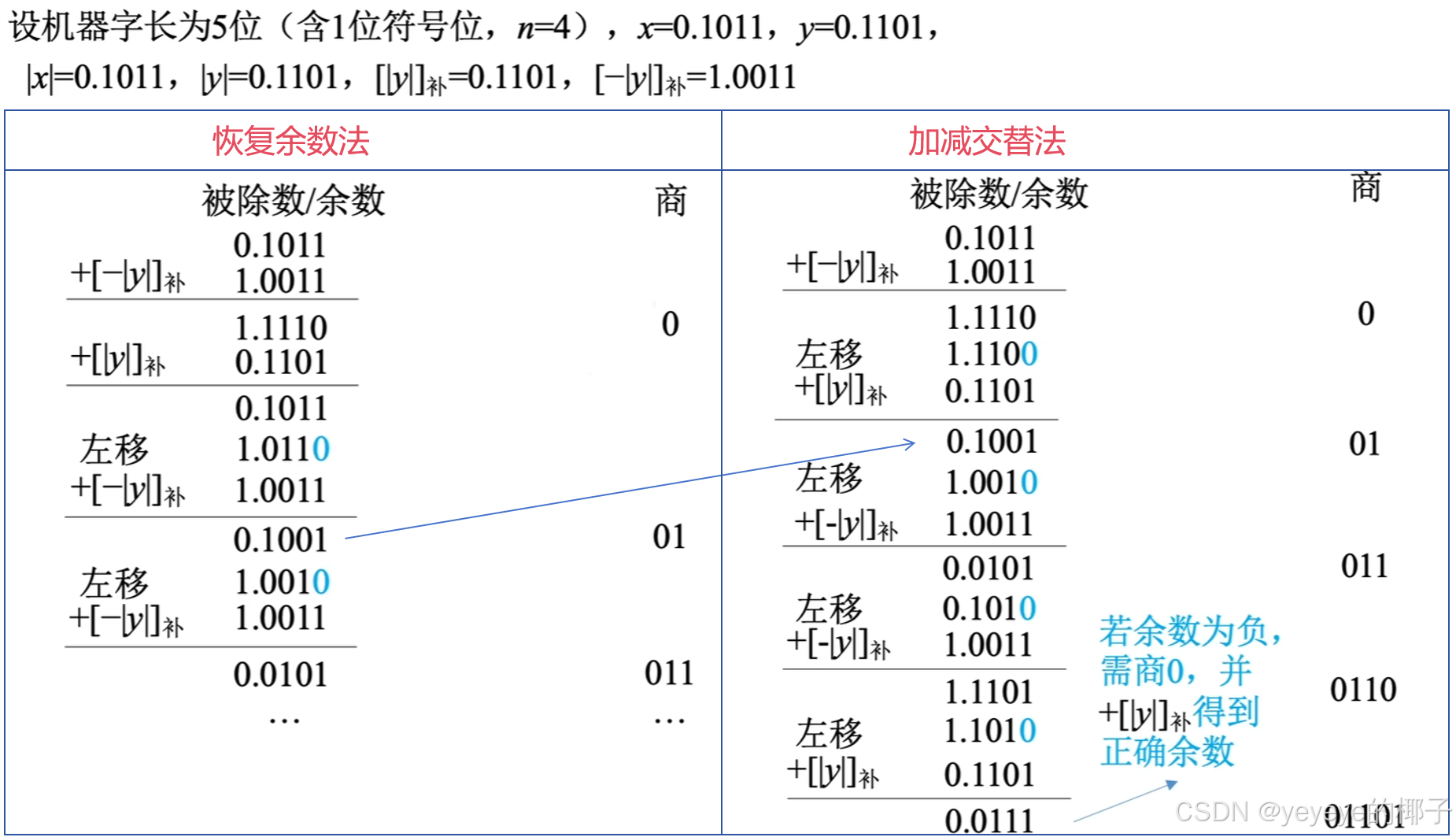
(2)补码除法:加减交替法
三、浮点数的表示和运算
1.浮点数的表示
(1)浮点数的表述形式
浮点数一般表示为:
- S取值0或1,用来决定浮点数的符号;
- M是一个二进制定点小数,称为尾数,一般用于原码小数表示;
- E是一个二进制定点整数,称为阶码或者指数,用移码表示。
- R是基数(隐含),可以约定为2、4、16等。
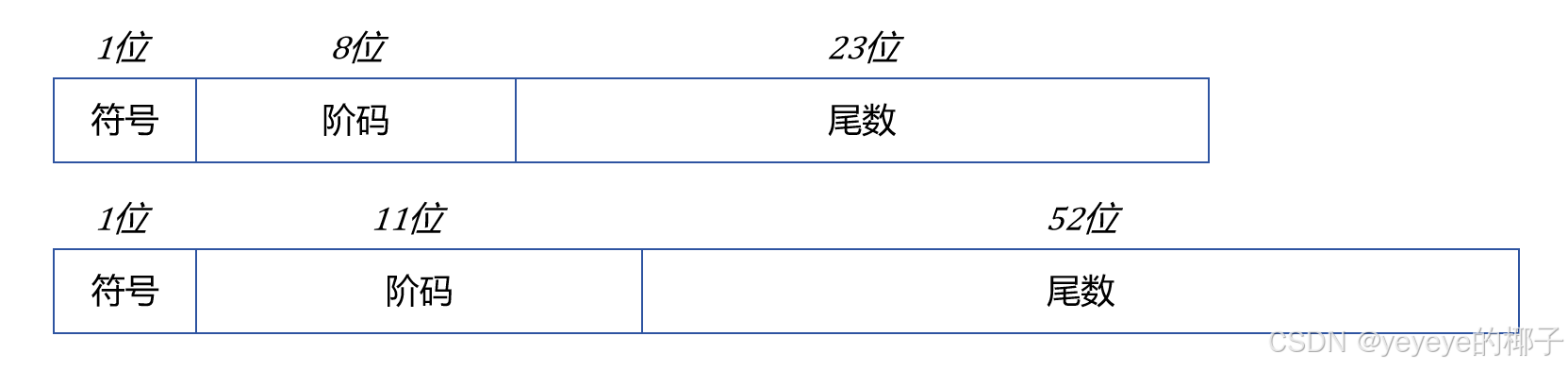
(2)IEEE754标准浮点数表示
IEEE754标准常用形式如下:
| 类型 | 符号s | 阶码e | 尾数f | 总位数 | 偏置值 | |
| 十六进制 | 十进制 | |||||
| 单精度 | 1 | 8 | 23 | 32 | 7FH | 127 |
| 双精度 | 1 | 11 | 52 | 64 | 3FFH | 1023 |
对于规格化的二进制浮点数,尾数的最高位总是1,为了能使尾数多表示一位有效位。在IEEE654规定隐藏位1的位置在小数点之前, 其整数部分的“1”将不存储在23位尾数内。
偏置值的作用是使得一个真数加上偏置值,即可得到移码的真值。偏置值为
.(其中n表示的是当前为n位移码)。列如一个浮点数的阶码为3,因此在单精度浮点数中,移码表示的阶码就是127+3=130(82H),在双精度浮点数中,阶码为1023+3=1026(402H)。
在其中对于阶码和尾数的不同情况下的解读:
- 全0阶码全0尾数:+0/-0。零的符号取决于符号s,一般情况下+0和-0是等效的。
- 全1阶码全0尾数:+∞/-∞。+∞在数值上大于所有有限数,-∞则小于所有有限数。引入无穷大数的目的是,在计算过程中出现异常情况可以使得程序继续进行下去。
- 全1阶码非0尾数:NaN(Not a Number)。表示一个没有定义的数,称为非数。
- 全0阶码非0尾数:非规格化数。非规格化数的隐藏位为0,尾数高位右一个或几个连续的0,但不全为0.因此,非规格化数的隐藏位为0,且单精度和双精度浮点数的指数分别是-126和-1022。非规格化数可以用于处理阶码下溢。
(3)浮点数的规格化
规格化的意义:为了在浮点数运算过程中尽可能多地保留有效数字地位数,使有效数字尽量占满尾数数位。
规格化操作:是指通过调整一个非规格化浮点数的尾数和阶码大小,使非零浮点数在尾数的最高数位上保证是一个有效值。
规格化的形式:有分为左规、右规来调整尾数和阶码。
左规:当运算结果的尾数的最高数位不是有效位时,需要进行左规。左规时,尾数每左移一位,阶码减1(基数为2时)。左规可能需要进行多次。列如:
右规:当运算结果的尾数的有效位进到小数点前面时,需要进行右规,右规只需要进行一次。将尾数右移一位、阶码加1(基数为2时)。右规时,阶码增加可能导致溢出。列如:
2.浮点数的加减法
浮点数的加减法主要分为下述几个步骤:
①对阶:对阶是让两个操作数的小数位置对齐,即使得两个数的阶码相等。
②尾数加减:在尾数相加减的时候需要先还原一下隐藏位“1”,再进行相加减。
③尾数规格化:在两个数相加减完毕后,其尾数不一定是规格化,需要进行左规或者右规。
④舍入:在对阶和尾数右规时,可能对尾数进行右移,可能会抛弃一些数值,影响精度,详细的舍入方法见下。
⑤溢出判断:查看左规或右规后,阶码部分是否是全1或者全0来判断的。
| 方法名 | 说明 |
| “0”舍“1”入 | 如果在右移的时候,被移除的最高数值为“0”,则舍去;被移除的最高数值为“1”,则在末尾加1。 |
| 恒置“1”法 | 尾数右移的时候,不论丢掉的最高数值位“1”还是“0”,都使右移后的尾数末尾恒置“1”。 |
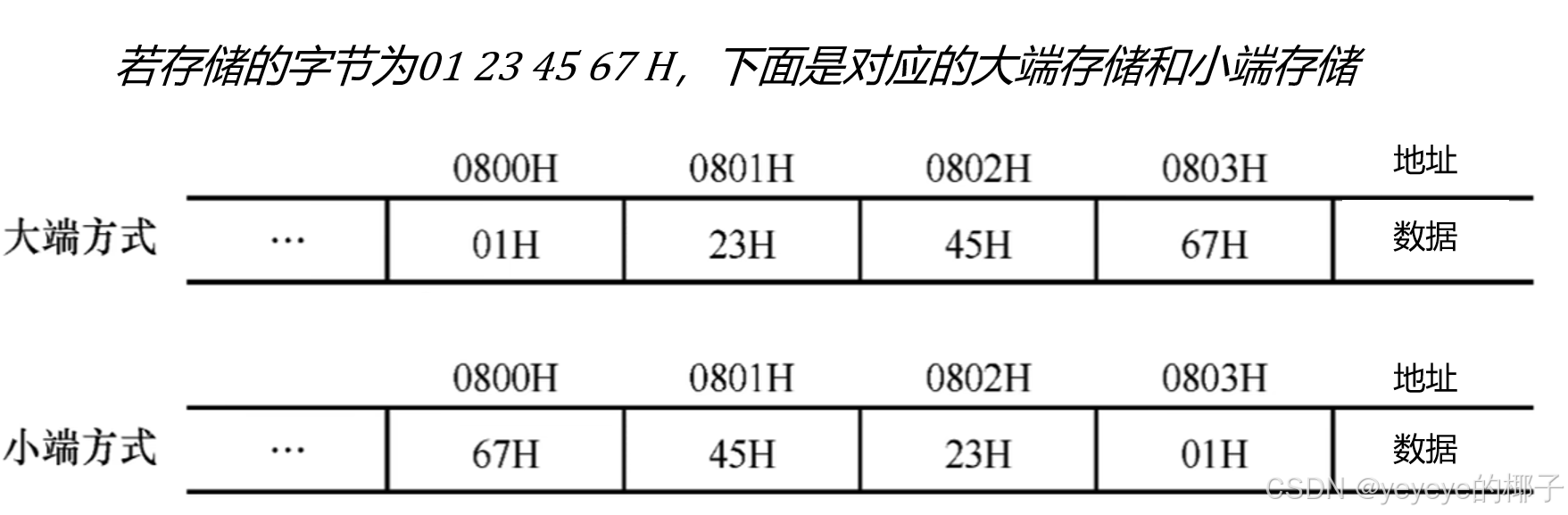
3.数据的大小端
- 大端存储:最高有效字节存储在低地址部分,最低有效字节存储在高地址部分,有利于人类阅读。字中字节顺序和原序列的相同。
- 小端存储:最低有效字节存储在低地址部分,最高有效字节存储在高地址部分,有利于机器处理。字中字节顺序和原序列的相反。
四、博主遇到题目的一些错误点
1.数值与编码
(1)对真值0表现形式唯一的是补码和移码
(2) 转反码的时候符号位不需要取反
(3)采用补码表示的时候,想要数值最大,就要让符号位为0,且把“1”放在最高位;要是使数值最小,就要让符号位为1,且把“1”放在低位
(4)若采用移码表示,要使数值最大,应该把“1”放在高位;要使数值最小,应该把“1”放在低位。移码的数值表示就是数值的实际大小。
(5)在计算机中通常用无符号数表示主存地址,因为主存地址一般都是正数,不需要符号位。
(6)当涉及到补码的位扩展的时候(列如:8位扩展到16位),是向8位的右侧,填充符号位的数值。列如:10100000 00000000(16位)拓展至11111111 11111111 10100000 00000000
(7)当涉及到无符号位扩展时,右侧填充相对应的“0” 即可
(8)在C语言中数据在内存中为补码表示形式。
(9)在题中遇到比大小这类问题,不要目测,如果考察补码之间比大小,一定要转换为原码来看下,别偷懒
2.运算方法和运算电路
(1)运算器由
算术逻辑单元(ALU
)、累加器
、状态寄存器
、通用寄存器
组等组成。地址寄存器是属于存储器部分。
(2)算术逻辑单元既可以做算数运算(加、减、乘等),也可以做逻辑运算(或、与、非等)
(3)负数补码进行算数移位的时候,左移补0(低位补0),右移补1(高位补1),(左0右1,同左0右火)。
(4)当遇到判断两个数做算术运算后有无溢出的题,可以先把两个数转为真值,看看是否可以在当前的位数下表示出来,超过表示范围则溢出。
(5)模4补码具有模2补码的全部优点且更容易姜茶加减运算中的溢出问题。储存模4码仅需要一个符号位。在正常情况下,模4补码的两个符号位总是相同的。
(6)当采用进位位来判断溢出时,当最高有效进位和符号位进位的值不相同时才产生溢出。
(7)原码乘法是先取操作数绝对值相乘,符号位单独处理
(8)在做减法时,是采用减数补码加上减数的负数的补码,低位的sub为1。
(9)对一个二进制左移,相当于对这个二进制乘上2;对一个二进制右移,相当于对这个二进制除上2。
五、结语
本文大多参考2025年计算机组成原理--王道考研辅导书






















 6038
6038

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








