高速显式非线性MPC实现

高速显式非线性模型预测控制

摘要

本文提出了一种面向电路的显式非线性模型预测控制 （NMPC）问题的近似解，该方法基于在单纯形域划分上定义的分段仿射函数。所得到的控制器适用于在可编程器件（如微控制器或现场可编程门阵列）中进行电路实现，从而使得 NMPC能够应用于采样时间较短的系统。所提出的方法通过硬件在环仿真进行了验证。

引言

模型预测控制（MPC）是一种成熟的基于模型的控制技术，适用于调节具有多个输入和输出的受约束系统[1],[2]。
在每个采样时刻，必须通过在线最小化成本指标来求解一个约束优化问题，以计算控制函数。对于线性系统，该优化问题是一个二次或线性规划（QP/LP）问题；而对于分段仿射（PWA）模型，它则是一个混合整数二次或线性规划问题。在这些情况下，可以通过多参数规划[3]–[5]在给定域内离线执行优化（显式模型预测控制）。所得到的控制律被证明是一个分段仿射函数。显式模型预测控制能够显著减少控制器的计算时间，因为在每个采样时刻仅需对一个分段仿射函数进行求值，而无需求解优化问题。
此外，已有许多技术被开发出来，以使显式模型预测控制更快，并适用于在具有较短采样时间的嵌入式系统上进行电路实现[6],[7]。例如，在[8]中，使用了定义在规则单纯形划分上的分段仿射函数来逼近精确的显式控制函数，这种结构特别适合快速电路实现。
对于非线性系统，与成本指标相关的优化问题是一个非线性规划（NLP）问题，该问题可能是非凸的并具有多个极小值，其求解在计算上可能过于复杂，难以在线实施。
人们已开发出多种用于非线性模型预测控制（NMPC）的算法：综述请参见[9],[10]及其参考文献。
在[11]中提出了一种高效的方法，用于求解最优反馈控制优化问题的在线近似解，称为实时迭代（RTI）方案。
在[12]中已为非线性规划（NLP）提供了显式的分段仿射（PWA）近似解。该技术允许实现通过二叉搜索树获得的控制器，从而避免了实时优化。
尽管已提出多种用于显式线性模型预测控制硬件实现的电路架构[13],[14]，但对于非线性模型预测控制，目前仅有少数隐式实现被提出[6],[15],[16]。
本文利用文献[8]中提出的方法，通过在一组点上计算精确的NMPC控制函数，并构建定义在单纯形域划分上的插值PWA函数（即分段仿射函数（PWAS）），实现近似。用于分段仿射函数（PWAS）的FPGA实现的电路架构已存在[13]，并且已有自动生成VHDL文件的自动化工具[17]。这使得获得能够实现极高的采样率（达到数十MHz量级）的近似嵌入式非线性模型预测控制成为可能。
所提出的近似分段仿射函数控制器已通过对受控范德波尔振荡器进行不同控制器复杂度的硬件在环仿真进行了测试。

II. 非线性模型预测控制

考虑一个非线性离散时间系统
$$ x_{k+1} = f(x_k, u_k) \tag{1} $$
受非线性约束
$$ h(x_k, u_k) \leq 0 \tag{2} $$
其中 $ x_k \in \mathbb{R}^n $ 和 $ u_k \in \mathbb{R}^m $ 分别表示在时间 $ kT_s $ 时的系统状态和输入，$ T_s $ 为系统的采样周期。

通过在每个采样时刻求解以下带有非线性约束的二次优化问题，可以获得用于跟踪系统状态至期望参考 $ x_r $ 的非线性模型预测控制控制动作：
$$
\min_U \sum_{i=0}^{N} e_{k+i|k}^T Q e_{k+i|k} + \sum_{i=0}^{N-1} u_{k+i}^T R u_{k+i} + \rho \varepsilon^2 \tag{3a}
$$
s.t.
$$
x_{k+i+1|k} = f(x_{k+i|k}, u_{k+i}), \quad i = 0,\dots,N \tag{3b}
$$
$$
h(x_{k+i|k}, u_{k+i}) \leq \varepsilon, \quad i = 0,\dots,N \tag{3c}
$$
$$
\varepsilon \geq 0 \tag{3d}
$$
其中 $ e = x - x_r $，符号 $ x_{k+i|k} $ 表示在给定时刻 $ kT_s $ 的状态下，时刻 $ (k+i)T_s $ 的预测状态。

从当前状态 $ x_k $ 和参考值 $ x_{r,k} $ 的测量值1出发，该问题的解是一个向量 $ U = [u_k, …, u_{k+N-1}] $，包含在给定时间范围 $ N $ 内的预测控制动作。仅第一个控制量 $ u_k $ 被实际施加到系统上，并在下一个采样时刻重复进行优化。其中，$ \varepsilon $ 是用于松弛约束的松弛变量，$ \rho $ 是一个较大的权重。引入 soft 约束使得解在任意域中可行，这是执行下一节所述的分段仿射函数（PWAS）近似的一个理想特性。连续时间系统在设计模型预测控制（MPC）控制器之前必须先进行离散化。第四节给出了一个示例。

可以采用多种策略来求解非线性规划问题[9]。在本文中，我们采用最简单的一种方法，称为逐次线性化方法。
代表非线性问题约束的方程(3b)和(3c)，在点 $ (x_k, u_k) $ 处通过一阶泰勒展开进行线性化，得到：
$$
x_{k+i+1|k} = J_x f(x_k, u_k)x_{k+i|k} + J_u f(x_k, u_k)u_{k+i} + f(x_k, u_k) - J_x f(x_k, u_k)x_k - J_u f(x_k, u_k)u_k \tag{4}
$$
$$
J_x h(x_k, u_k)x_{k+i|k} + J_u h(x_k, u_k)u_{k+i} \leq -h(x_k, u_k) + J_x h(x_k, u_k)x_k + J_u h(x_k, u_k)u_k + \varepsilon \tag{5}
$$
其中，$ J_x f $ 和 $ J_x h $ 分别表示函数 $ f $ 和 $ h $ 的雅可比矩阵中涉及系统状态的部分，而 $ J_u f $ 和 $ J_u h $ 是涉及系统输入的部分。

通过将式(4)和式(5)代入式(3b)和式(3c)，并在 $ f $ 和 $ h $ 相对于 $ u_k $ 为线性的条件下，问题(3)转化为一个带约束的二次规划问题，该问题可利用任意二次规划算法轻松求解。
需要指出的是，下一节所述的近似显式控制器的设计与求解非线性规划问题所采用的方法无关。

III. 近似显式非线性模型预测控制

分段仿射函数（PWAS）是定义在被划分为单纯形的域上的分段仿射函数。一个超矩形域 $ D \subset \mathbb{R}^n $ 按如下方式被划分为单纯形：$ D $ 的每个维度分量被划分为 $ p_i $ 个子区间；因此，该域被划分为 $ \prod_{i=1}^{n} p_i $ 个超矩形，其 $ V $ 个顶点表示为 $ v_i $、$ i = 1,…, V $。每个超矩形再通过一类三角剖分[8]被进一步划分为 $ n! $ 个互不重叠的单纯形。如果所有超矩形均相同，则该单纯形划分为均匀的。本文仅使用均匀划分，其中每个域分量被划分为 $ p_i = P $（$ i = 1,…,n $）个段。这使得能够在不引入不必要复杂性的情况下更好地描述该方法。推广到任意单纯形划分是直接的。

分段仿射函数（PWAS）$ \hat{u}: D \rightarrow \mathbb{R}^m $ 可以表示为分段仿射基函数的线性组合：
$$
\hat{u}(z) = \sum_{i=1}^{V} w_i \alpha_i(z) \tag{6}
$$
如果系统状态无法测量，则必须采用观测器对其进行估计。

第 $ i $ 个函数 $ \alpha_i $ 是以单纯形划分的第 $ i $ 个顶点 $ v_i $ 为中心的超锥体。该函数在 $ v_i $ 处取值为1，在所有其他顶点处取值为0。采用此类基函数时，有[8]：
$$
w_i = \hat{u}(v_i) \tag{7}
$$
一旦确定了划分，分段仿射函数（PWAS）即由权重 $ w_i $ 唯一确定。在[8]中，分段仿射函数（PWAS）被用于近似显式模型预测控制的控制函数，该控制函数本身是定义在多面体划分上的分段仿射函数。在该论文中，通过最小化表示精确控制律与近似控制律之间距离的二次代价函数来获得权重 $ w_i $。由于需要计算涉及多次评估精确显式控制函数的积分，该方法计算量较大。

由于在非线性模型预测控制中，精确控制函数的求值需要求解问题(3)，本文采用了一种更简单的方法，基于插值而非逼近。优化问题的输入为状态 $ x_k $ 和参考值 $ x_{r,k} $，因此所得的分段仿射函数将定义为 $ \hat{u} k(x_k, x {r,k}) $。一旦每维的细分数量 $ P $ 确定，单纯形划分的顶点 $ v_i $ 即可自动获得。
在顶点 $ v_i $ 处求解问题(3)，得到精确的控制值 $ u_i = u(v_i) $。
根据公式(7)，权重 $ w_i $（从而分段仿射函数）被确定为 $ w_i = u_i $。需要注意的是，由于引入了软约束，问题(3)的解始终是可行的，因此精确控制函数在所有划分顶点上均有定义。

用于分段仿射函数控制函数的FPGA实现的电路架构在[13]中有所描述，这些架构也可用于本应用，从而实现快速嵌入式非线性模型预测控制控制器的设计。

然而，插值必然导致控制性能的下降。此外，一般来说，精确控制器的稳定性和鲁棒性保证也会丧失。该方法的另一个问题，也是任何显式模型预测控制解决方案普遍存在的问题，即所谓的维数灾难，因为顶点数量（以及相应的存储空间）随着域维度的增加呈指数增长，使得该方法仅适用于相对较小的系统（最多4‐5个维度），且要求较低的采样周期。这一问题可以通过采用非均匀单纯形划分[18]来部分克服。

IV. 结果

上一节所述技术应用于阻尼范德波尔振荡器的控制，其连续时间状态方程为[19]
$$
\begin{cases}
\dot{x}_1 = x_2 \
\dot{x}_2 = \mu(1 - x_1^2)x_2 - Bx_2 - x_1 + k_f u
\end{cases}
\tag{8}
$$
其中 $ \mu = 1 $、$ B = 0.1 $ 和 $ k_f = 100 $。控制器的目标是确保状态 $ x_1 $ 跟踪一个期望参考 $ r $，而 $ x_2 $ 被调节为0（即 $ x_r = [r\ 0]^T $）。为了验证精确和近似 NMPC 处理约束的能力，已对系统状态和输入施加了以下限制：
$$
0 \leq x_1 \leq 5 \tag{9a}
$$
$$
-8 \leq x_2 \leq 8 \tag{9b}
$$
$$
-1 \leq u \leq 1 \tag{9c}
$$

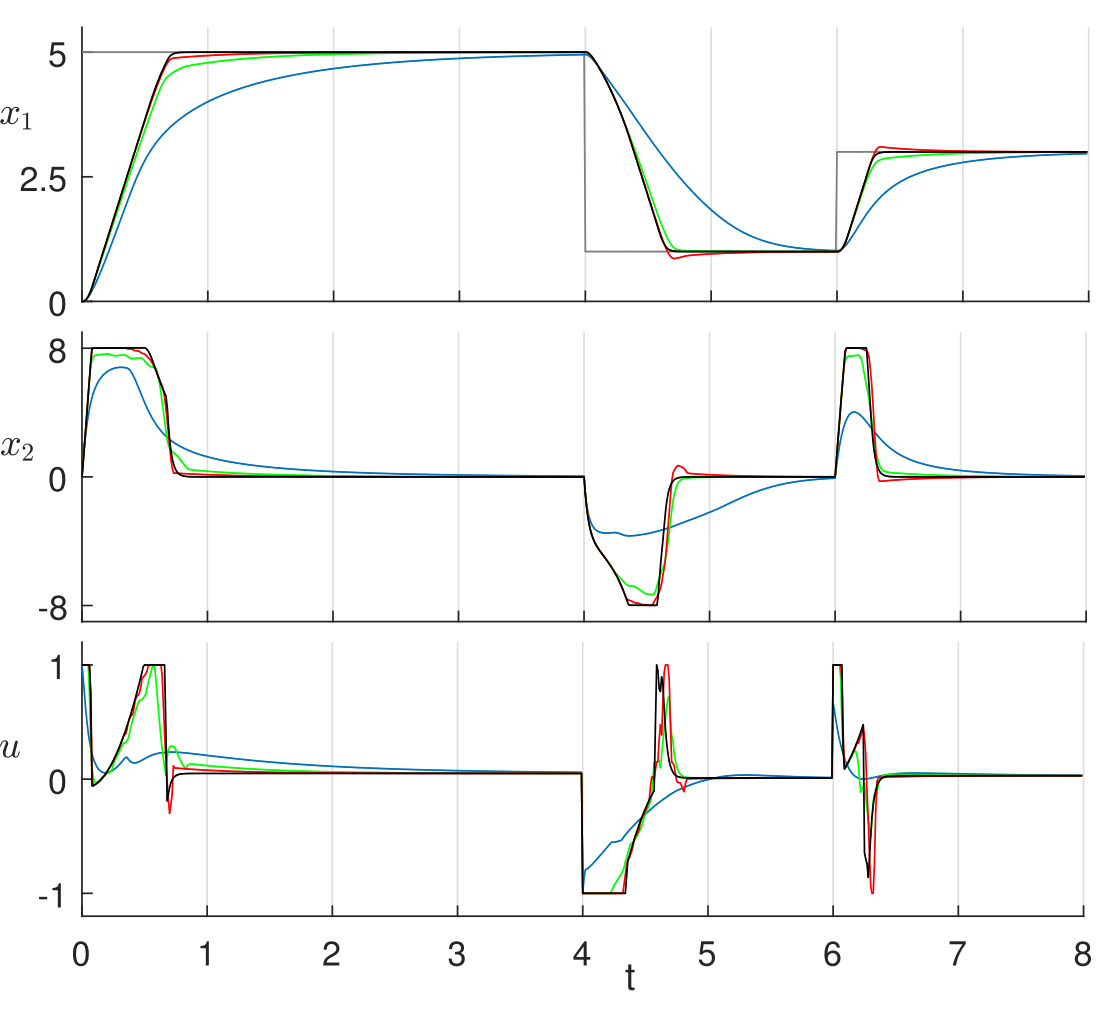
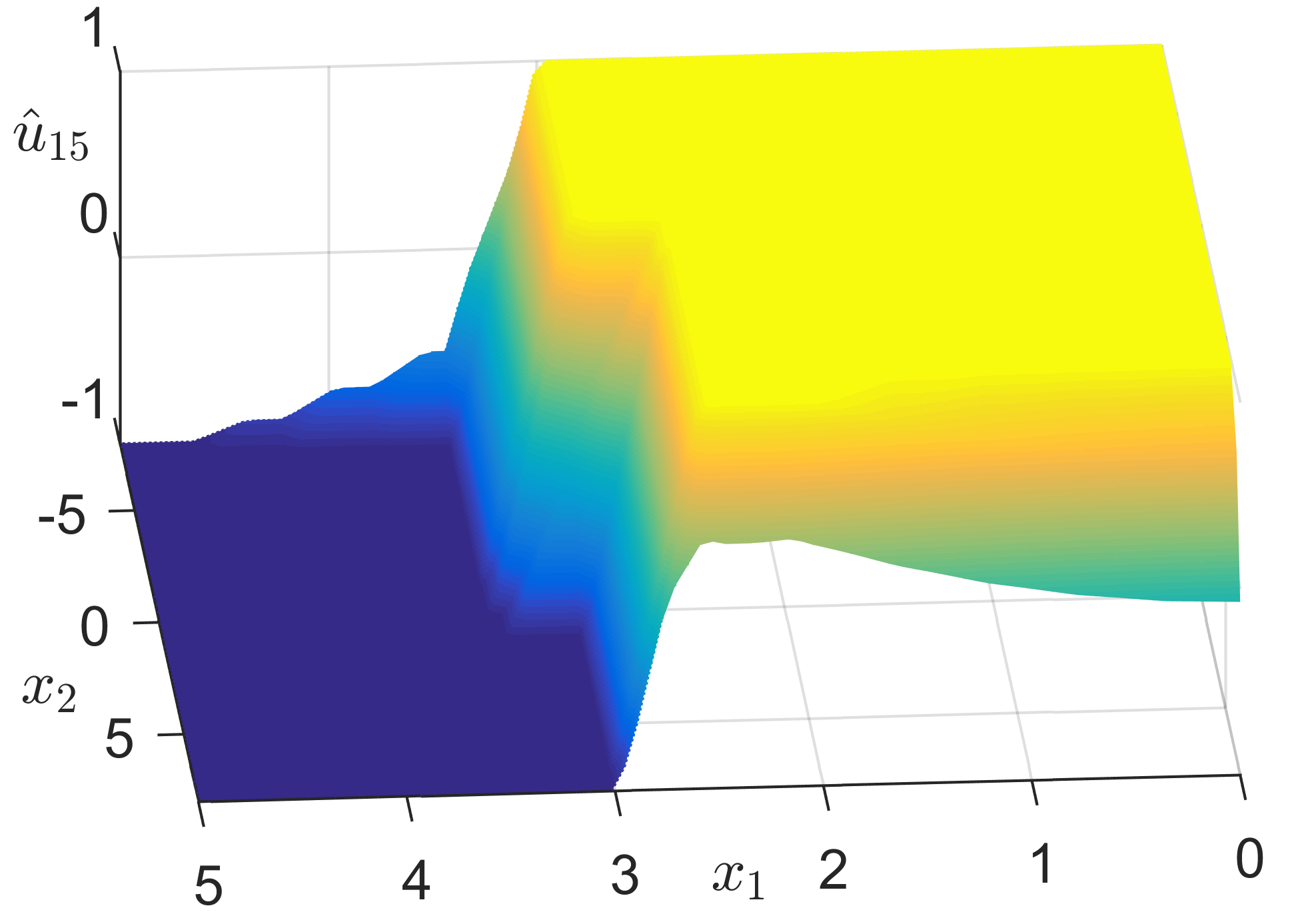
在以采样时间 0.01 秒对范德波尔系统方程进行离散化后，通过在当前状态下对系统动态进行线性化，并设置 $ N = 5 $、$ Q = \begin{bmatrix} 10^3 & 0 \ 0 & 1 \end{bmatrix} $、$ R = 10^{-3} $ 和 $ \rho = 10^6 $，求解了非线性模型预测控制（NMPC）问题（3）。选择这些值的目的是实现快速收敛且无超调，如图1所示，其中显示了由精确NMPC控制函数控制的闭环系统的状态和输入随时间的变化（黑色线条）。优化问题的输入为 $ x_1 $、$ x_2 $ 和 $ r $，因此任何近似的分段仿射函数（PWAS）控制函数均定义在一个三维域上。设计了三个定义在均匀单纯形划分上的分段仿射函数 $ \hat{u} 3 $、$ \hat{u}_7 $ 和 $ \hat{u} {15} $，其划分节点数分别为 $ P = 3 $、7 和 15。图2展示了函数 $ \hat{u}_{15} $ 在 $ r = 3 $ 的二维截面上的图像。

用于控制函数的FPGA实现的VHDL文件已通过 MOBY-DIC 工具箱[17]生成，所得到的电路架构（在[13]中描述）已在低成本的 Spartan 3 XC3S200 FPGA 上实现。电路输入、输出和系数采用定点12位分辨率。所有电路均使用4个12位乘法器，并具有12个时钟周期的延迟。

函数	% 片段	最大频率	延迟	最大 $ f_s $
$ \hat{u}_3 $	19	100 MHz	120 ns	8.3 MHz
$ \hat{u}_7 $	24	95 MHz	126 ns	7.9 MHz
$ \hat{u}_{15} $	46	70 MHz	171 ns	5.8 MHz

表 I 三种PWAS控制器的电路性能

表I显示了占用的现场可编程门阵列切片百分比、可达到的最大时钟频率、相应的电路延迟以及可达到的最大采样频率 $ f_s = 1/T_s $。所有功能均适配于所选的小型现场可编程门阵列，并能够实现非常低的计算时间。

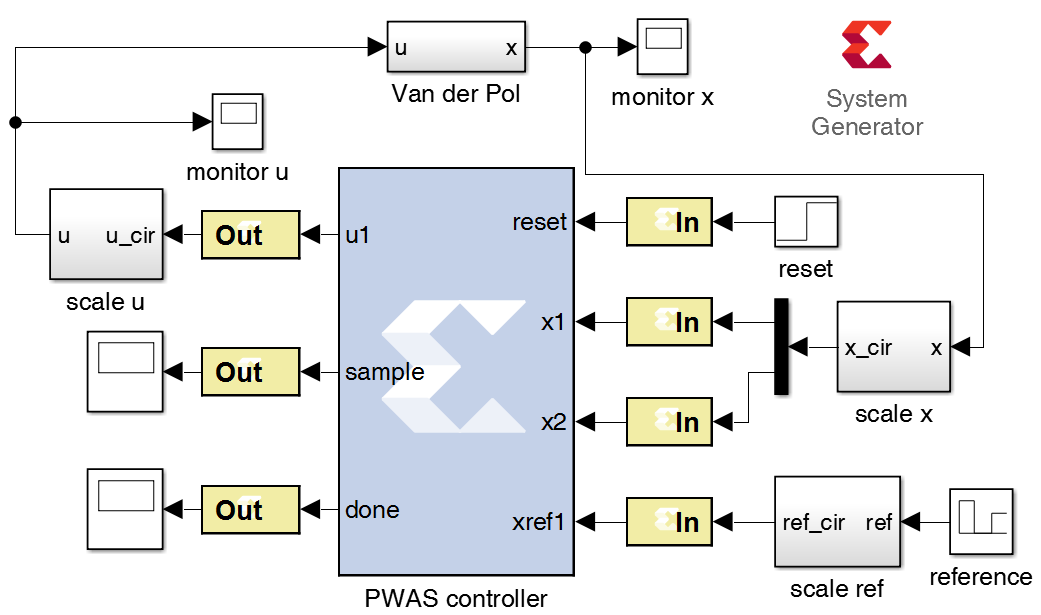
通过Simulink和Xilinx系统生成器进行了硬件在环（HIL）仿真，其模块示意图如图3所示。由函数 $ \hat{u} 3 $、$ \hat{u}_7 $ 和 $ \hat{u} {15} $ 控制的系统(8)的硬件在环（HIL）仿真结果分别用蓝色、绿色和红色线条表示，如图1所示。顶部图中的灰色线条为参考状态 $ r $。

首先可以看出，所有控制器都能通过满足约束(9)将系统状态调节至其参考值。控制函数 $ \hat{u} 3 $ 实现了最快且最小的电路架构，但在调节速度方面的性能表现较差。使用 $ \hat{u}_7 $ 可获得更好的结果。控制函数 $ \hat{u} {15} $ 能够实现几乎相同的控制性能与精确控制律相同，仅在调节 $ x_1 $ 至 $ r = 1 $ 和 $ r = 3 $ 时存在小幅超调。因此，在所考虑的三种近似方法中，分段仿射函数（PWAS）$ \hat{u}_7 $ 在控制精度和电路复杂度之间实现了最佳折衷。

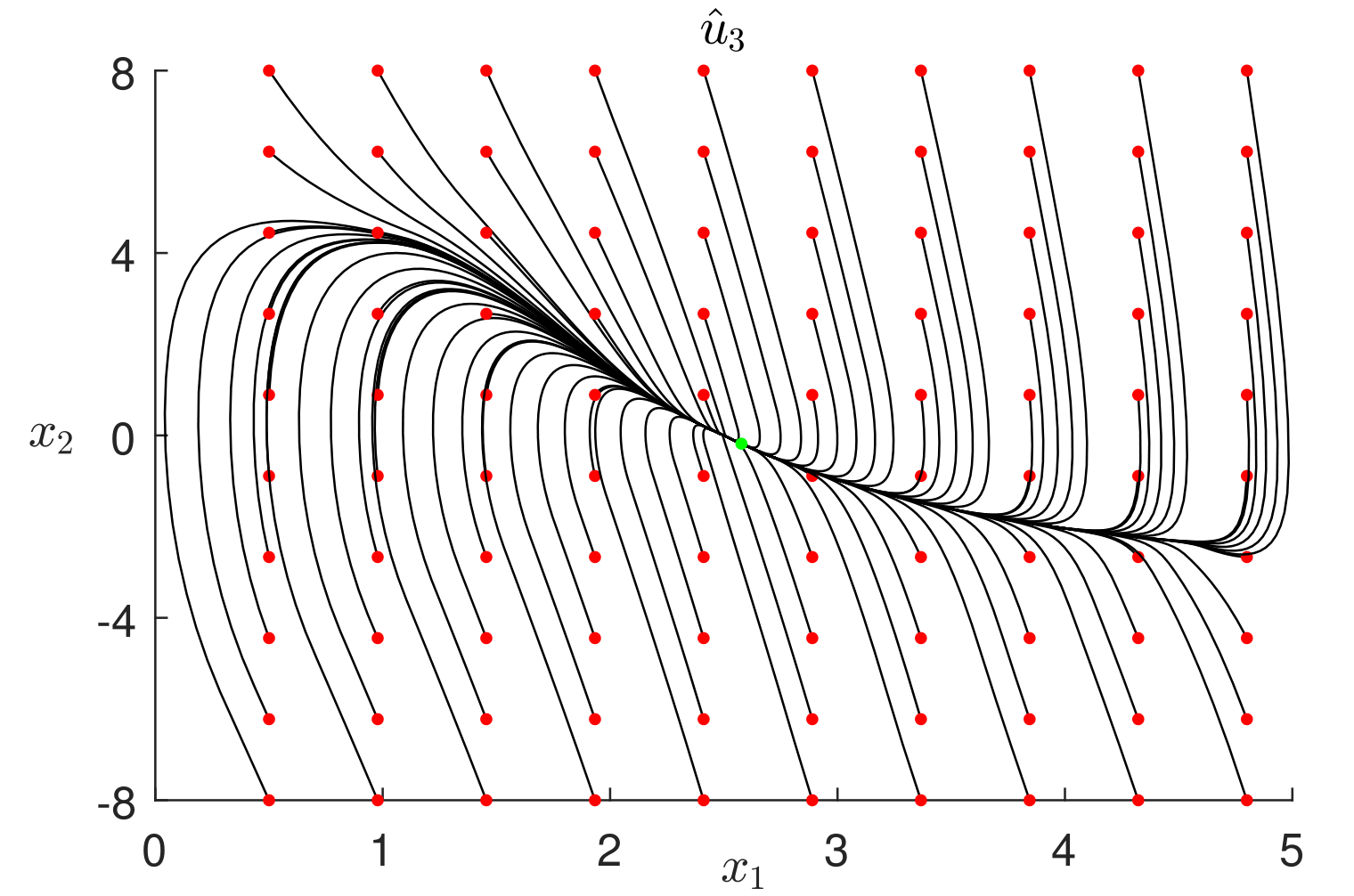
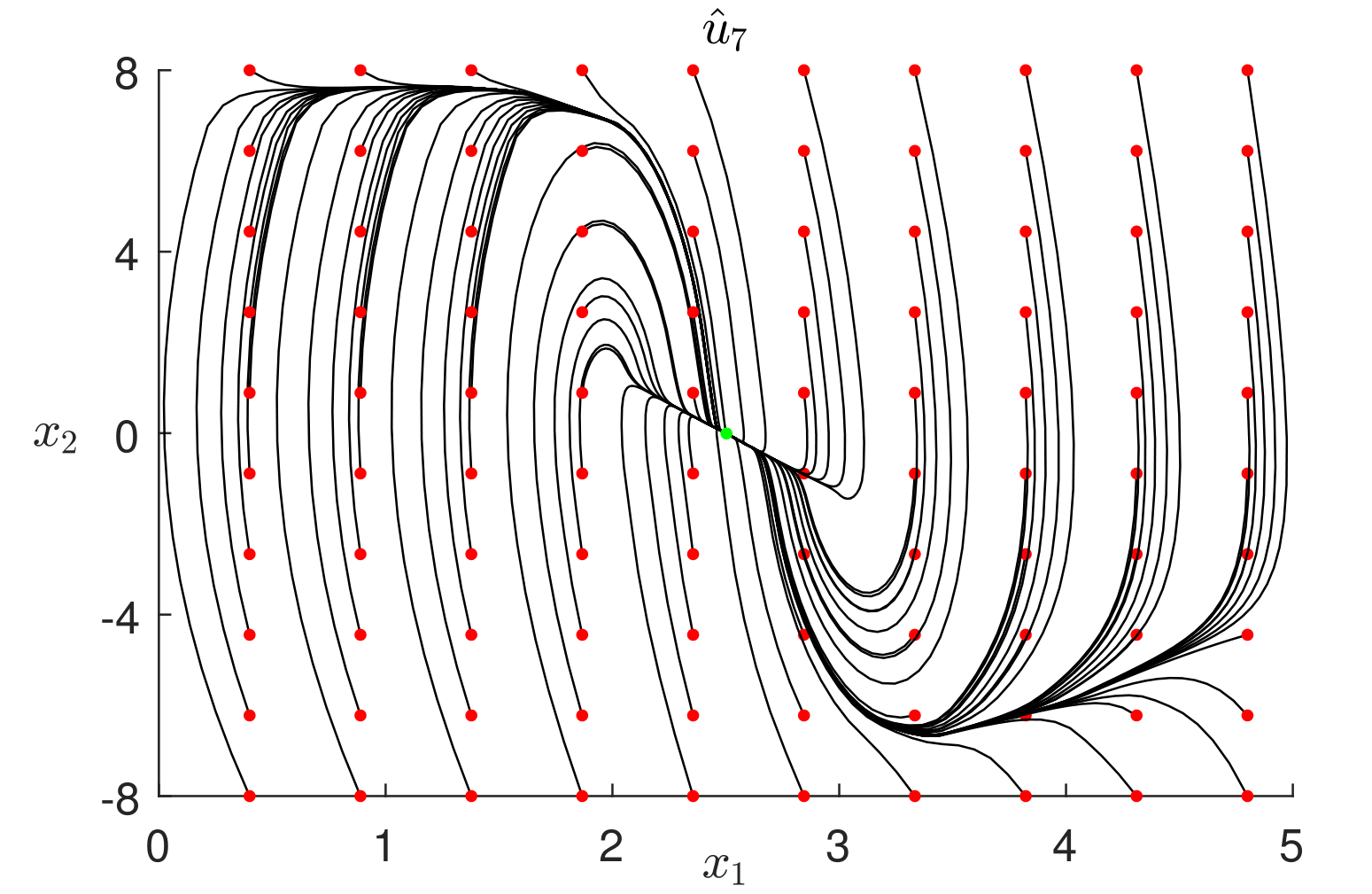
通过改变初始条件（绿点 $ r = 2.5 $）进行了进一步的仿真。图4和图5分别展示了从系统(8)的100个不同初始条件（红点）出发，在控制律 $ \hat{u}_3 $ 和 $ \hat{u}_7 $ 作用下的状态相图。
在所有情况下，调节均正确执行，并满足所施加的约束条件。

五、结论

分段仿射函数（PWAS）已成功应用于求解非线性模型预测控制问题的近似显式解。已有文献中的电路架构被用于在现场可编程门阵列上实现近似控制器。所提出的方法通过涉及Simulink和Spartan3 FPGA的硬件在环仿真，对Van der Pol振荡器的跟踪进行了测试。设计了三个精度逐步提高的近似控制器，复杂度，并比较了它们的控制和电路性能。

一方面，所得到的结果表明，该方法能够以非常低的计算时间实现正确的控制动作。这是所提出策略的主要优势。另一方面，这种近似会带来控制性能的损失。此外，稳定性与鲁棒性保证可能不再得到确保。