决策树

1 决策树

分类决策树模型是一种描述对实例进行分类的树形结构。决策树由结点（node）和有向边（directed edge）组成。结点有两种类型：内结点（internal node）和叶子结点（leaf node）。内部结点表示一个特征或属性，叶结点表示一个类。

用决策树分类，从根结点开始，对实例的某一特征进行测试，根据测试结果，将实例分配到其子结点；这时，每一个子结点对应着该特征的一个取值。如此递归地对实例进行测试并分配，直至达到叶结点。最后将实例分到叶结点的类中。

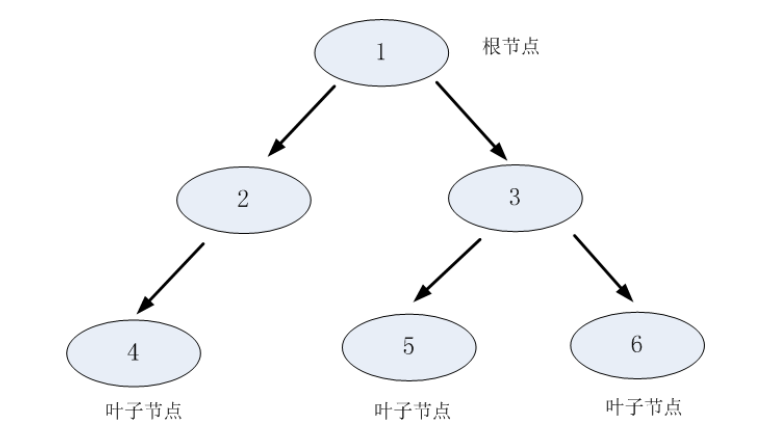
决策树的构建是数据逐步分裂的过程，构建的步骤如下:

1. 将所有的数据看成是一个节点，进入步骤2；
2. 从所有的数据特征中挑选一个数据特征对节点进行分割，进入步骤3；
3. 生成若干子节点，对每一个子节点进行判断，如果满足停止分裂的条件，进入步骤4；否则，进入步骤2；
4. 设置该节点是子节点，其输出的结果为该节点数量占比最大的类别。

通过以上步骤，我们可以看出需要解决的两个问题：如何选择分裂的特征；停止分裂的条件是什么。

2 信息论基本概念

• 熵
  在信息论与概率统计中，熵（entropy）是表示随机变量不确定性的度量。设$X$是一个取有限个值的离散随机变量，其概率分布为$P\left(X=x_i\right)=p_i$，则随机变量X的熵定义为：$$H(X)=-\sum _{i=1}^n{p}_i\log p_i$$
• 条件熵
  条件熵$H(Y|X)$表示在已知随机变量X的条件下随机变量Y的不确定性。随机变量X给定的条件下随机变量Y的条件熵（conditional entropy）$H(Y|X)$，定义为X给定条件下Y的条件概率分布的熵对X的数学期望：$$H(Y|X)=\sum _{i=1}^{n}P\left(X=x_i\right)H(Y|X=x_i)$$
• 信息增益
  特征A对训练数据集D的信息增益$g(D,A)$，定义为集合D的经验熵$H(D)$与特征A给定条件下D的条件熵$H(D|A)$之差$$g(D,A)=H(D)-H(D|A)$$
• 信息增益比
  特征A对训练数据集D的信息增益比$g_R(D,A)$定义为其信息增益$g(D,A)$与训练数据集D的经验熵H(D)之比$$g_R(D,A)=\frac{g(D,A)}{H(D)}$$
• 基尼指数
  分类问题中，假设有K个类，样本点属于第k类的概率为$p_k$，则概率分布的基尼指数定义为$$\mathrm{Gini}(p)=\sum _{k=1}^K{p}_k\left(1-p_k\right)=1-\sum _{k=1}^K{p}_k^2$$对于给定的样本集合D，$C_k$是D中属于第k类的样本子集，K是类的个数，则其基尼指数为$$\mathrm{Gini}(D)=1-\sum _{k=1}^K{\left(\frac{\left|C_k\right|}{|D|}\right)}^2$$如果样本集合D根据特征A是否取某一可能值a被分割成D1和D2两部分，则在特征a的条件下，集合D的基尼指数定义为$$\mathrm{Gini}(D,A)=\frac{\left|D_1\right|}{|D|}\mathrm{Gini}\left(D_1\right)+\frac{\left|D_2\right|}{|D|}\mathrm{Gini}\left(D_2\right)$$基尼指数值越大，样本集合的不确定性也就越大，这一点与熵相似，但是Gini指数的计算不需要对数运算，更加高效，同时Gini 指数更偏向于连续属性，而熵更偏向于离散属性。

3 ID3算法

ID3算法的核心是在决策树各个结点上应应信息增益准则选择特征，递归地构建决策树。

具体方法是：

1. 从根结点(root node)开始，对结点计算所有可能的特征的信息增益，选择信息增益最大的特征作为结点的特征。
2. 由该特征的不同取值建立子节点，再对子结点递归地调用以上方法，构建决策树；直到所有特征的信息增益均很小或没有特征可以选择为止；
3. 最后得到一个决策树。

假设我们有训练数据集D，特征集A，阈值$\sigma$，输出决策树为T，则ID3算法如下：

1. 若D中所有实例属于同一类$C_k$，则T为单结点树，并将类$C_k$作为该结点的类标记，返回T；
2. 若A＝Ø，则T为单结点树，并将D中实例数最大的类Ck作为该结点的类标记，返回T；
3. 否则，计算A中各特征对D的信息增益$g(D,A)$，选择信息增益最大的特征$A_g$；
4. 如果$A_g$的信息增益小于阈值$\sigma$，则置T为单结点树，并将D中实例数最大的类$C_k$作为该结点的类标记，返回T；
5. 否则，对$A_g$的每一可能值$a_i$，依$A_g=a_i$将D分割为若干非空子集$D_i$，将$D_i$中实例数最大的类作为标记，构建子结点，由结点及其子结点构成树T，返回T；
6. 对第i个子结点，以$D_i$为训练集，以$A-A_g$为特征集，递归地调用步（1）～步（5）得到子树Ti，返回Ti。

优点：结构简单、清晰易懂、灵活方便
缺点：分裂精确度不够高；不能处理缺省值；没有对决策树进行剪枝处理，很可能会出现过拟合的问题；不能对连续数据进行处理，只能通过连续数据离散化进行处理

4 C4.5算法

C4.5在ID3的基础上对上述三个方面进行了相应的改进：

• C4.5对节点进行分裂时采用信息增益率作为分裂的依据；
• 能够对连续数据进行处理，能够处理具有缺失属性值的训练数据
• C4.5采用剪枝的策略，对完全生长的决策树进行剪枝处理，一定程度上降低过拟合的影响

5 CART

根据训练数据集，从根结点开始，递归地对每个结点进行以下操作，构建二叉决策树：

1. 设结点的训练数据集为D，计算现有特征对该数据集的基尼指数。此时，对每一个特征A，对其可能取的每个值a，根据样本点对A＝a的测试为“是”或“否”将D分割成D1和D2两部分，并计算A＝a时的基尼指数。
2. 在所有可能的特征A以及它们所有可能的切分点a中，选择基尼指数最小的特征及其对应的切分点作为最优特征与最优切分点。依最优特征与最优切分点，从现结点生成两个子结点，将训练数据集依特征分配到两个子结点中去。
3. 对两个子结点递归地调用（1），（2），直至满足停止条件。
4. 生成CART决策树。
   算法停止计算的条件是结点中的样本个数小于预定阈值，或样本集的基尼指数小于预定阈值（样本基本属于同一类），或者没有更多特征。

CART的剪枝：

1. 设$\mathrm{k}=0,\mathrm{T}={\mathrm{T}}_0，\alpha =+\infty$ 。
2. 自下而上地对各内部结点t计算$C(T_t)$，$|T_t|$以及$g(t)=\frac{C(t)-C\left(T_t\right)}{|T_t|-1}$，$\alpha =\min (\alpha ,g(t))$
3. 自上而下地访问内部结点t，如果有$g(t)＝\alpha$，进行剪枝，并对叶结点t以多数表决法决定其类，得到树T。
4. 设$\mathrm{k}=\mathrm{k}+1$,${\alpha }_{\mathrm{k}}=\alpha$,${\mathrm{T}}_{\mathrm{k}}=\mathrm{T}$
5. 如果T不是由根结点单独构成的树，则回到步骤3
6. 采用交叉验证法在子树序列中选取最优子树$T_{\alpha }$

6 剪枝

剪枝是指从已经生成的树上裁掉一些子树或叶节点，并将其根节点或父节点作为新的叶子节点，从而简化分类树模型。通过极小化决策树整体的损失函数或代价函数来实现，即选择损失函数最小的子树。

决策树学习的损失函数定义为：$$C_{\alpha }(T)=\sum _{t=1}^{|T|}{N}_t{H}_t(T)+\alpha |T|$$其中，各项代表的意义如下：

• T：表示这棵子树的叶子节点，
• $H_t(T)$：表示第t个叶子的熵$H_t(T)=-{\sum }_k\frac{N_{tk}}{N_t}\log \frac{N_{tk}}{N_t}$
• $N_t$：表示该叶子所含的训练样例的个数

决策树的剪枝过程（泛化过程）就是从叶子节点开始递归，记其父节点将所有子节点回缩后的子树为$T_b$（分类值取类别比例最大的特征值），未回缩的子树为$T_a$，如果$C_{\alpha }\left(T_a\right)\ge C_{\alpha }\left(T_b\right)$说明回缩后使得损失函数减小了，那么应该使这棵子树回缩，递归直到无法回缩为止，这样使用“贪心”的思想进行剪枝可以降低损失函数值，也使决策树得到泛化。

7 Sklearn

sklearn.tree.DecisionTreeClassifier

• criterion
  特征选择标准 ‘gini’ or ‘entropy’ (default=”gini”)
  前者是基尼系数，后者是信息熵。两种算法差异不大对准确率无影响，信息墒云孙效率低一点，因为它有对数运算.一般说使用默认的基尼系数”gini”就可以了，即CART算法。除非你更喜欢类似ID3, C4.5的最优特征选择方法。
• splitter
  特征划分标准 ‘best’ or ‘random’ (default=”best”)
  前者在特征的所有划分点中找出最优的划分点。后者是随机的在部分划分点中找局部最优的划分点。 默认的”best”适合样本量不大的时候，而如果样本数据量非常大，此时决策树构建推荐”random” 。
• max_depth
  决策树最大深度 int or None, optional (default=None)
  一般来说，数据少或者特征少的时候可以不管这个值。如果模型样本量多，特征也多的情况下，推荐限制这个最大深度，具体的取值取决于数据的分布。常用的可以取值10-100之间。常用来解决过拟合
• min_impurity_decrease
  节点划分最小不纯度 float, optional (default=0.)
  这个值限制了决策树的增长，如果某节点的不纯度(基尼系数，信息增益，均方差，绝对差)小于这个阈值，则该节点不再生成子节点。 sklearn 0.19.1版本之前叫 min_impurity_split
• min_samples_split
  内部节点再划分所需最小样本数 int, float, optional (default=2)
  如果是 int，则取传入值本身作为最小样本数； 如果是 float，则去 ceil(min_samples_split * 样本数量) 的值作为最小样本数，即向上取整。
• min_samples_leaf
  叶子节点最少样本数
  如果是 int，则取传入值本身作为最小样本数； 如果是 float，则去 ceil(min_samples_leaf * 样本数量) 的值作为最小样本数，即向上取整。 这个值限制了叶子节点最少的样本数，如果某叶子节点数目小于样本数，则会和兄弟节点一起被剪枝。
• max_leaf_nodes
  最大叶子节点数 int or None, optional (default=None)
  通过限制最大叶子节点数，可以防止过拟合，默认是”None”，即不限制最大的叶子节点数。如果加了限制，算法会建立在最大叶子节点数内最优的决策树。如果特征不多，可以不考虑这个值，但是如果特征分成多的话，可以加以限制，具体的值可以通过交叉验证得到。
• min_impurity_split
• 信息增益的阀值 决策树在创建分支时，信息增益必须大于这个阀值，否则不分裂
  min_weight_fraction_leaf 叶子节点最小的样本权重和 float, optional (default=0.) 这个值限制了叶子节点所有样本权重和的最小值，如果小于这个值，则会和兄弟节点一起被剪枝。 默认是0，就是不考虑权重问题。一般来说，如果我们有较多样本有缺失值，或者分类树样本的分布类别偏差很大，就会引入样本权重，这时我们就要注意这个值了。
• class_weight
  类别权重 dict, list of dicts, “balanced” or None, default=None
  指定样本各类别的的权重，主要是为了防止训练集某些类别的样本过多，导致训练的决策树过于偏向这些类别。这里可以自己指定各个样本的权重，或者用“balanced”，如果使用“balanced”，则算法会自己计算权重，样本量少的类别所对应的样本权重会高。当然，如果你的样本类别分布没有明显的偏倚，则可以不管这个参数，选择默认的”None” 不适用于回归树