数据结构（十 八）之字符串类的实现

1.1 字符串类的设计
1.1.1 继承关系图

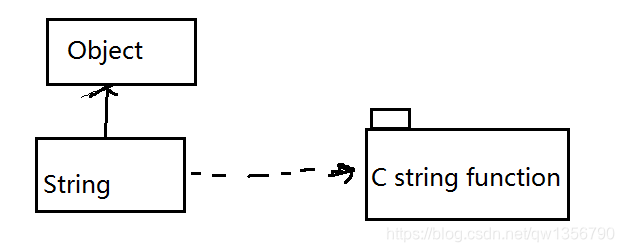
1.1.2 字符串类的实现

1.1.3 注意事项

• 无缝实现String对象和 char * 字符串的互操作
• 操作符重载函数需要考虑是否支持const 版本
• 通过C语言中的字符串函数实现String的成员函数

1.2字符串中常用的成员函数

1.2.1成员函数

成员函数	功能描述
operator[]	操作符重载函数，访问指定下标的字符
startWith(s)	判断字符串是否以s开头
endOf(s)	判断字符串是否以S结尾
insert(i,s)	在字符串的位置i处插入s
trim()	去掉字符串两端的空白

1.2.2操作符重载函数

    char& operator[](int i);
    char operator[](int i) const;

• 注意事项
  • 当i的取值不合法时，抛出异常
  • 合法范围： （ 0 <= i） && （i < m_length）

1.2.3 函数声明

class String : public Object
{
protected:
   char* m_str;
   int m_length;

   void init(const char* s);
   bool equal(const char* l, const char* r, int len) const;
public:
    String();
    String(char c);
    String(const char* s);
    String(const String&s);

    int length() const;
    const char* str() const;

    bool operator == (const String& s)const;
    bool operator == (const char* s)const;
    bool operator != (const String& s)const;
    bool operator != (const char* s)const;
    bool operator > (const String& s)const;
    bool operator > (const char* s)const;
    bool operator < (const String& s)const;
    bool operator < (const char* s)const;
    bool operator >= (const String& s)const;
    bool operator >= (const char* s)const;
    bool operator <= (const String& s)const;
    bool operator <= (const char* s)const;

    String operator + (const String& s) const;
    String operator + (const char* s) const;
    String& operator += (const String& s);
    String& operator += (const char* s);

    String& operator = (const String& s);
    String& operator = (const char* s);
    String& operator = (char c);

    char& operator[](int i);
    char operator[](int i) const;

    bool startWith(const char* s) const;
    bool startWith(const String&s) const;

    bool endOf(const char* s) const;
    bool endOf(const String&s) const;

    String& insert(int i, const char* s);
    String& insert(int i, const String&s);

    String& trim();     // 为啥是返回引用，因为可以这样使用 s2.trim().str()


    ~String();

};

1.2.4 思考

• 如何在目标字符重查找是否存在指定的子串 ?

String s = "zhangsan";
int pos = s.indexof("san"); // pos = 5 

1.3KMP 算法

1.3.1

• 如何在目标字符重查找是否存在指定的子串 ?
  

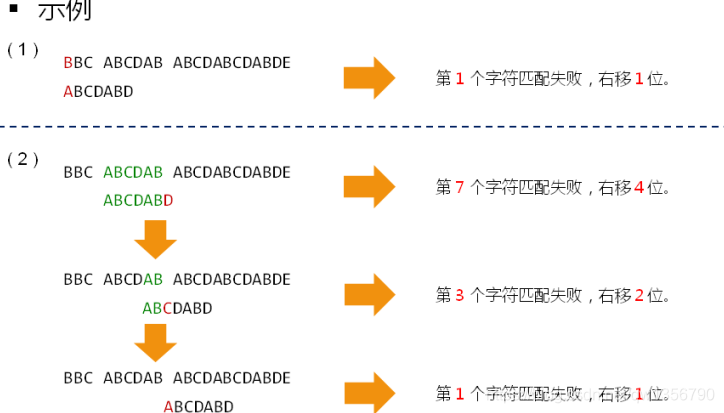
1.3.2 伟大的发现

• 匹配失败时的右移位数与子串本身相关， 和目标串无关
• 移动位数 = 已匹配的字符数 - 对应的部分匹配值
• 任意子串都存在一个唯一的部分匹配值

1.3.3 部分匹配表示例

1	2	3	4	5	6	7
A	B	C	D	A	B	D
0	0	0	0	1	2	0

• 用法
  
• 第7 位 匹配失败----> 前6 位匹配成功----> 查表PMT[6]
  ----> 右移位数6 - PMT[6] = 6 - 2 = 4;
• 当我们知道部分匹配表就可以很清楚的知道，当匹配失败的时候，我们可以知道跳过几个字符

1.3.4 部分匹配如何获取

• 前缀： 除了最后一个字符以外，一个字符串的全部头部组合
• 后缀： 除了第一个字符以外，一个字符串的全部尾部组合
• 部分匹配值： 前缀和后缀最长共有元素的长度
• 举例：
  
• 示例：

0	字符	前缀	后缀	交集	匹配值
1	A	空	空	空	0
2	AB	A	B	空	0
3	ABC	A，AB	C,BC	空	0
4	ABCD	A，AB，ABC	D，CD，BCD	空	0
5	ABCDA	A,AB,ABC,ABCD	BCDA,CDA,DA,A	A	1
6	ABCDAB	A,AB,ABC,ABCD,ABCDA	BCDAB,CDAB,DAB,AB,B	AB	2
7	ABCDABD	A,AB,ABC,ABCD,ABCDA,ABCDAB	省略	空	0

1.3.5 部分匹配如何产生

• 实现关键
  • PMT[1] =0 （下标为0 的元素匹配值为0）
  • 从第二个字符开始递推（从下标为1的字符开始递推）
  • 假设PMT[N] = PMT[n - 1] + 1 (·最长共有元素的长度）
  • 当假设不成立，PMT[n]在PMT[n - 1]的基础上减小

1.4
1.4.1部分匹配表实现

• 代码实现

int* make_pmt(const char* p)
{
    int len = strlen(p);
    int* ret = static_cast<int*> (malloc(sizeof(int) * len));
    if(ret != NULL)
    {
        int ll = 0;  // longest length
        ret[0] = 0;
        for(int i =1; i < len; i++)
        {
            while((ll > 0) && (p[ll] != p[i]))
            {
                ll = ret[ll - 1];
            }
            if(p[ll] == p[i])
            {
                ll++;
            }
            ret[i] = ll;
        }
    }

    return ret;
}
int main()
{
    // ababax
    int* pmt = make_pmt("ABCDABD");
    for(int i = 0; i < strlen("ABCDABD"); i++)
    {
        cout << i << " : " << pmt[i] << endl;
    }
    return 0;
}

1.4.2 KMP的实现

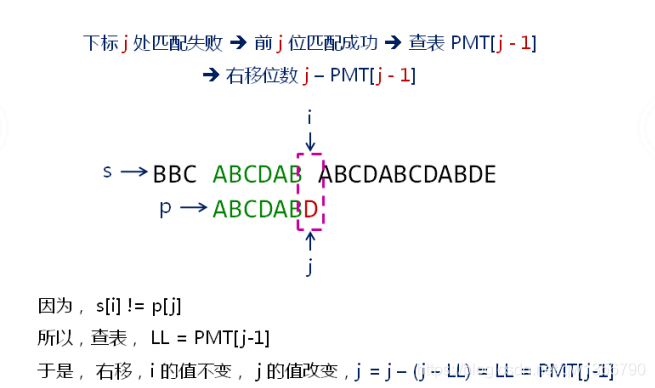
• 代码实现

int kmp(const char* s, const char* p)
{
    int ret = -1;
    int sl =strlen(s);
    int pl =strlen(p);
    
    int * pmt = make_pmt(p);
    if((pmt != NULL) && (0 < pl) && ( pl < sl))
    {
        for(int i =0,j =0; i < sl; i++)
        {
            while((j > 0) && (s[i] != p[j]))
            {
                j = pmt[j - 1];
            }
            if(s[i] = p[j])
            {
                j++;
            }
            if( j == pl)
            {
                ret = i + 1 - pl;
                break;
            }
        
        }    
    }
    free(pmt);
    
    return ret; 

}

int main()
{
    cout << kmp("zhangsan","zhangsan") << endl;
    return 0;
}

1.5 KMP算法的应用
1.5.1 字符串类中的新功能

成员函数	功能
indexOf(s)	查找子串s在字符串中位置
remove(s)	将字符串中的子串s删除
operator - (s)	定义字符串减法
replace(s,t)	将字符串中的子串替换为t
sub(i, len)	从字符串中创建子串

参考一 : 狄泰软件课程

如有侵权：请联系邮箱 1986005934@qq.com