计算器
首先要设置相应的按键
包括±*/()AC CE等运算符
步骤一:
以下为设置按键
void buttonZeroClicked();
void buttonOneClicked();
void buttonTwoClicked();
void buttonThreeClicked();
void buttonFourClicked();
void buttonFiveClicked();
void buttonSixClicked();
void buttonSevenClicked();
void buttonEightClicked();
void buttonNineClicked();
void buttonAddClicked();//+
void buttonSubClicked();//-
void buttonMulClicked();//乘
void buttonDivClicked();//除
void buttonTimClicked(); //时间
void buttonDecClicked();//小数点
void buttonBotClicked(); //加减号
void buttonEquClicked();//等于号
void buttonLefClicked();//左括号
void buttonRigClicked();//右括号
void buttonCEClicked();//CE
void buttonACClicked();//AC
步骤二:
设置优先级
int level(char ch) {//给每一个运算符附上优先级
switch(ch) {
case ‘(’ :
return 5;
case ‘*’ :
return 4;
case ‘/’ :
return 4;
case ‘+’ :
return 3;
case ‘-’ :
return 3;
case ‘)’:
return 2;
}
}
步骤三:
中缀表达式转为后缀表达式
核心思想:
大致思路是
要先给运算符定义相应的优先级。然后取出最开始输入的式子,依次判断式子中的数字和运算符。
如果是数字则直接放入v中。
如果栈为空则压入栈中
如果是运算符则要分情况讨论
1如果当前的运算符是),则之前压在地下的运算符必须依次弹出到v中,直到遇到(,然后把(删掉并且)也不压入。
2如果当前的运算符不是(,则遇到比自己小的,下面的运算符也要弹出到v中。
3如果当前的运算符比之前的大,则压入栈中
最终,栈中剩余的运算符依次弹到v中
/由中缀表达式得到后缀表达式, 向量V存储结果/
vector midToPost(string s) {
stack S; /符号栈/
vector V; /后缀表达式/
int i = 0;
while(i < s.length()) {
if(isNum(s[i])) { //如果这个字符属于整数、浮点数或复数的表示,返回True,否则返回False.
string str = “”;//定义一个新的字符串
while(isNum(s[i]) || s[i] == ‘.’) {
str += s[i];//字符串拼接
i++;
}//可以得到两位及以上或带小数点的数
V.push_back(str);//在vector的末尾插入一个元素
}
else if(isOperate(s[i])){//如果这个字符属于操作符返回true
/负数情况/
if(s[i] == ‘-’ && (i == 0 || !isNum(s[i-1]))) { //如果-为首位或者-前面的值不为数字
string str = “-”; i++;
while(isNum(s[i]) || s[i] == ‘.’) {
str += s[i]; i++;
}
V.push_back(str);
}else{
if(S.empty()){ //栈为空
S.push(s[i]); i++;
}else {
int initial = level(s[i]);//当前s[i]的优先级
if(initial == 2) { //情况一:如果符号为)优先级最低
while(level(S.top()) != 5 && !s.empty()) {//把栈中存放的除(外的运算符均弹到v中
string str = “”;
str += S.top();//把栈顶元素赋值给str
V.push_back(str);
S.pop();//消除栈顶元素
}
if(S.top() == ‘(’) S.pop();//当)刚好碰到优先级最高的(
i++;
} else {
while(!S.empty() && initial <= level(S.top()) && level(S.top()) != 5) {//情况二:倘若优先级不为)且当前的s[i]比栈中的优先级要小
string str = “”;
str += S.top();
V.push_back(str);
S.pop();
}
S.push(s[i]);//情况三:当前s[i]优先级比栈中的情况要大
i++;//符号压栈
}
}//对应的是判断运算符
}//栈为空和判断运算符
}
else{//不满足以上则代表有问题
cout << "表达式出错" << endl;
V.clear();
return V;
}
}
while(!S.empty()) {//最后留在栈中的也要逐一弹到v中
string str = ""; str += S.top();
S.pop();
V.push_back(str);
}
//for(int i = 0; i < V.size(); i++) cout << V[i] << "[]";
return V;
}
步骤四:
后缀表达式输出最后结果:
大致思想
通过不断遍历v,先把v中的元素全部从字符变成数值型,然后依次压入新定义的s栈中,之后通过遍历s中的栈顶弹出依次取出相应的数和运算符。
/后缀表达式得到最终结果/
double getValue(vector V) { //vector是一个能够存放任意类型的动态数组
stack S;
for(int i = 0; i < V.size(); i++) {
/操作运算符/
if(V[i].length() == 1 && isOperate(V[i][0])) {//v[i]为一个字符时,并且是数字
double a = 0, b = 0;
if(!S.empty()) { //如果栈不为空
a = S.top(); S.pop();
}else return INT_MAX;
if(!S.empty()) {//如果堆栈不为空
b = S.top(); S.pop();
}else return INT_MAX;
switch(V[i][0]) { //数后面必为运算符
case ‘+’:
S.push(b+a);
break;
case ‘-’:
S.push(b-a);
break;
case '’:
S.push(ba);
break;
case ‘/’:
S.push(b/a);
break;
default:
return INT_MAX;
}
}else {//栈为空时
if(scd(V[i]) == INT_MAX) return INT_MAX;
else S.push(scd(V[i]));//把v中的全部压入栈中
}
}//操作V
if(S.empty()) return INT_MAX;
double value = S.top();
S.pop();
return value;
}
/字符串转数字/
double scd(string s) { //
if(s.length() == 0) return INT_MAX;
bool flag = false;
for(int i = 0; i < s.length(); i++) {
if(i == 0 && s[i] == ‘-’) continue;//负数的情况
else if(s[i] == ‘.’ && !flag) {
if(i > 0 && isNum(s[i-1])) {//小数点
flag = true;
continue;
}
else return INT_MAX;
}
else if(isNum(s[i])) continue;//数值
else return INT_MAX;
}
double result = atof(s.c_str());//把字符串转为浮点数
return result;
}
结果展示:
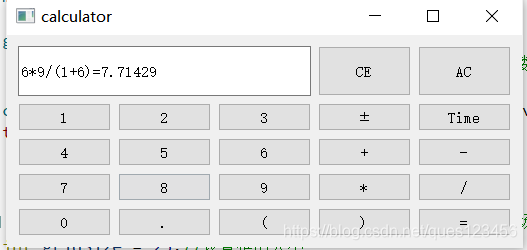




 本文介绍了计算器的实现过程,包括设置按键、定义运算符优先级、中缀表达式转后缀表达式以及后缀表达式求值的核心算法。通过解析输入的中缀表达式,将其转换为后缀表达式,再计算得出结果。
本文介绍了计算器的实现过程,包括设置按键、定义运算符优先级、中缀表达式转后缀表达式以及后缀表达式求值的核心算法。通过解析输入的中缀表达式,将其转换为后缀表达式,再计算得出结果。
















 788
788

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








