Datawhale X 李宏毅苹果书 AI夏令营《深度学习详解》第一章机器学习基础-优快云博客

本文链接：https://blog.youkuaiyun.com/qq_74869852/article/details/141575382

机器学习，顾名思义，机器具备有学习的能力。具体来讲，机器学习就是让机器具备找一个函数的能力。随着要找的函数不同，机器学习有不同的类别：

回归（输出是一个数值，一个标量）
分类（输出是从设定好的选项里面选择一个当作输出）结构化学习（机器不只是要做选择题或输出一个数字，而是产生一个有结构的物体，比如让机器画一张图，写一篇文章）

1.1 案例学习

机器学习找函数的过程分为三个步骤：

1、写出一个带有未知参数的函数f

比如将函数写成 $y=b+wx_{1}$ ， $y$ 是准备要预测的东西， $b$ 和 $w$ 是未知的参数， $b$ 称为偏置（bias）， $w$ 称为权重（weight），特征 $x_{1}$ 是函数里面已知的变量。我们将带有未知的参数（parameter）的函数称为模型（model）。

2、定义损失（loss）

损失也是一个函数，这个函数的输入是模型里面的参数，由上可知模型为 $y=b+wx_{1}$ ，由于 $b$ 和 $w$ 是未知的，所以损失函数是 $L(b,w)$

其中， $N$ 代表训验数据的个数，即 3 年来的训练数据，就 365 乘以 3，计算出一个 $L$ ， $L$ 是每一笔训练数据的误差 $e$ 相加以后的结果。 $L$ 越大，代表现在这一组参数越不好， $L$ 越小，代表现在这一组参数越好。

估测的值其实和实际的值之间的差距其实有不同的算法：

平均绝对误差（Mean Absolute Error，MAE）公式为： $e=\left | \hat{y} -y\right |$ ；
均方误差（Mean SquaredError，MSE）公式为： $e=\left ( \hat{y}-y \right )^{2}$ ;
有一些任务中 $y$ 和 $\hat{y}$ 都是概率分布，这个时候可能会选择交叉熵（cross entropy）

也可以画出等高线图，越偏红色系，代表计算出来的损失越大；如果越偏蓝色系，就代表损失越小，尝试不同的参数计算损失画出来的等高线图称为误差表面（error surface）

3、解一个最优化的问题

找到使得损失 $L$ 最小的参数 $b$ 和 $w$ ，代表他们是最优的一组，通常优化采用梯度下降（gradient descent）的方法，以一个参数变化为例先进行解释。

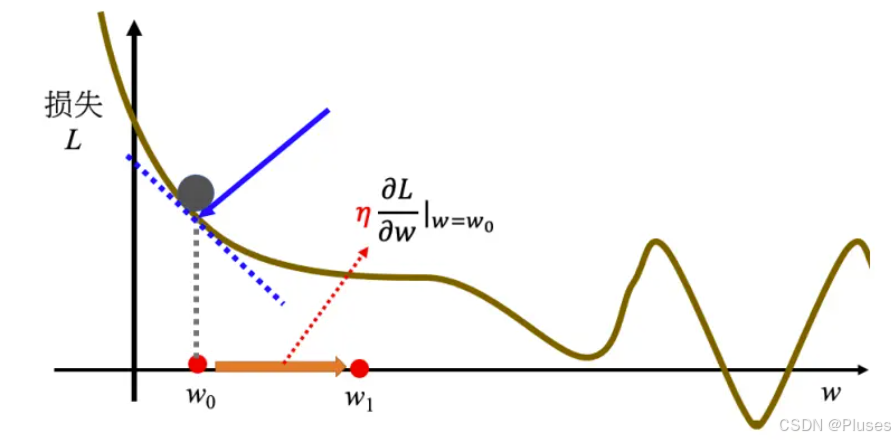
首先要随机选取一个初始的点 $w^{0}$ 。

接下来计算 $\frac{\partial L}{\partial w}|_{w=w^{0}}$ ，在 $w$ 等于 $w^{0}$ 的时候，参数 $w$ 对损失的微分。计算在这一个点，在 $w^{0}$ 这个位置的误差表面的切线斜率，也就是这一条蓝色的虚线它的斜率。

如果这一条虚线的斜率是负的，代表说左边比较高，右边比较低，就把 $w$ 的值变大，就可以让损失变小；
如果算出来的斜率是正的，就代表左边比较低，右边比较高，就代表把 $w$ 变小， $w$ 往左边移，可以让损失的值变小。

其中， $w$ 变化的大小取决于两个事情：

这个点的斜率，斜率越大 $w$ 越大，斜率越小 $w$ 越小
学习率（learning rate） $\eta$ 也会对其产生影响。学习率是自己设定的，如果 $\eta$ 设大一点，每次参数更新就会量大，学习可能就比较快；如果 $\eta$ 设小一点，参数更新就很慢，每次只会改变一点点参数的数值。这种在做机器学习，需要自己设定，不是机器自己找出来的，称为超参数（hyperparameter）

把 $w^{0}$ 往右移一步，新的位置为 $w^{1}$ ，这一步的步伐是 $\eta$ 乘上微分的结果，即：

$w^{1}\leftarrow w^{0}-\eta \frac{\partial L}{\partial w}|_{w=w^{0}}$

接下来反复进行刚才的操作，计算一下 $w^{1}$ 微分的结果，再决定现在要把 $w^{1}$ 移动多少，再移动到 $w^{2}$ ，再继续反复做同样的操作，不断地移动 $w$ 的位置，最后会有两种情况停下来：

一种情况是最开始将更新次数设定成了超参数
还有另外一种理想上的，当不断调整参数，调整到一个地方，它的微分的值就是这一项，算出来正好是 0 的时候，如果这一项正好算出来是 0，0 乘上学习率 $\eta$ 还是 0，所以参数就不会再移动位置。假设是这个理想的情况，把 $w^{0}$ 更新到 $w^{1}$ ，再更新到 $w^{2}$ ，最后更新到 $w^{T}$ 有点卡， $w^{T}$ 卡住了，也就是算出来这个微分的值是 0 了，参数的位置就不会再更新。

梯度下降法会有一个问题，可能走到 $w^{T}$ 时，训练就停止了，但是 $w^{T}$ 只是一个局部最小值（local minima），其左右两边都比这个地方的损失还要高一点，但是它不是整个误差表面上面的最低点，即 $w^{T}$ 这个点还不是全局最小值（global minima）

将梯度下降的方法推广到两个参数变化：

假设有两个参数，随机初始值为 $w^{0}$ ， $b^{0}$ 。要计算 $w$ ， $b$ 跟损失的微分，计算在 $w=w^{0}$ 的位置， $b=b^{0}$ 的位置，要计算 $w$ 对 $L$ 的微分，计算 $b$ 对 $L$ 的微分：

$\frac{\partial L}{\partial b}|_{w=w^{0} ,b=b^{0}}$ ， $\frac{\partial L}{\partial w}|_{w=w^{0},b=b^{0}}$

计算完后更新 $w$ 跟 $b$ ，把 $w^{0}$ 减掉学习率乘上微分的结果得到 $w^{1}$ ，把 $b^{0}$ 减掉学习率乘上微分的结果得到 $b^{1}$ ：

$w^{1}\leftarrow w^{0}-\eta \frac{\partial L}{\partial w}|_{w=w^{0},b=b^{0}}$ ， $b^{1}\leftarrow b^{0}-\eta \frac{\partial L}{\partial b}|_{w=w^{0},b=b^{0}}$

1.2 线性模型

把输入的特征 x 乘上一个权重，再加上一个偏置就得到预测的结果，这样的模型称为线性模型（linear model）

1、分段线性曲线

线性模型有很大的限制，这种来自于模型的限制称为模型的偏差，无法模拟真实的情况。所以需要写一个更复杂的、更有灵活性的、有未知参数的函数。

所以红色线，即分段线性曲线（piecewise linear curve）可以看作是一个常数，再加上一堆蓝色的函数。

也许要考虑的x跟y的关系不是分段线性曲线，而是一条曲线。可以在这样的曲线上面，先取一些点，再把这些点点起来，变成一个分段线性曲线。而这个分段线性曲线跟原来的曲线，它会非常接近，如果点取的够多或点取的位置适当，分段线性曲线就可以逼近这一个连续的、有角度的、有弧度的这一条曲线。

所以可以用分段线性曲线去逼近任何的连续的曲线，而每个分段线性曲线都可以用一大堆蓝色的函数组合起来。也就是说，只要有足够的蓝色函数把它加起来，就可以变成任何连续的曲线。

假设 $x$ 跟 $y$ 的关系非常复杂也没关系，就想办法写一个带有未知数的函数。直接写 Hard Sigmoid 不是很容易，但是可以用一条曲线来理解它，用 Sigmoid 函数（S型的函数）来逼近 Hard Sigmoid。

Sigmoid 函数的表达式为： $y=c\frac{1}{1+e^{-\left ( b+wx_{1} \right )}}$ ，其横轴输入是 $x_{1}$ ，输出是 $y$ ， $c$ 为常数。如果 $x_{1}$ 的值，趋近于无穷大的时候， $e^{-\left ( b+wx_{1} \right )}$ 这一项就会消失，当 $x_{1}$ 非常大的时候，这一条就会收敛在高度为 $c$ 的地方。如果 $x_{1}$ 负的非常大的时候，分母的地方就会非常大， $y$ 的值就会趋近于 0。

调整函数中的 $b$ ， $w$ 和 $c$ 可以制造各种不同形状的Sigmoid 函数，把不同的Sigmoid 函数叠起来以后就可以去逼近各种不同的分段线性函数，各种不同的分段线性函数就可以用来近似各种不同的连续的函数。

此外，我们可以不只用一个特征 $x_{1}$ ，可以用多个特征代入不同的 $c$ , $b$ , $w$ ，组合出各种不同的函数，从而得到更有灵活性（flexibility）的函数。Sigmoid 越多可以产生有越多段线的分段线性函数，可以逼近越复杂的函数。Sigmoid 的数量也是一个超参数。

利用矩阵和向量相乘的方法计算更加具有灵活性的函数。

接下来要定义损失。现在未知的参数多了，再把它一个一个列出来太累了，所以直接用 $\theta$ 来统设所有的参数，所以损失函数就变成 $L\left ( \theta \right )$ ，损失函数能够判断 $\theta$ 的好坏，其计算方法与上文方法相同。

但实现上有个细节的问题，实际使用梯度下降的时候会把 N 笔数据随机分成一个一个的批量（batch），每个批量里面有 B 笔数据，现在只拿一个批量里面的数据出来算一个损失，记为 $L_{1}$ 跟 $L$ 以示区别。假设 B 够大，也许 $L$ 跟 $L_{1}$ 会很接近。所以实现上每次会先选一个批量，用该批量来算 $L_{1}$ ，根据 $L_{1}$ 来算梯度，再用梯度来更新参数，接下来再选下一个批量算出 $L_{2}$ ，根据 $L_{2}$ 算出梯度，再更新参数，以此类推。

所以并不是拿 $L$ 来算梯度，实际上是拿一个批量算出来的 $L_{1}$ ， $L_{2}$ ， $L_{3}$ 来计算梯度。把所有的批量都看过一次，称为一个回合（epoch），每一次更新参数叫做一次更新。更新跟回合的区别，用两个例子来说明：

假设有 10000 笔数据，即 N 等于 10000，批量的大小设 10，也就是 B 等于 10。10000 个样本（example）形成了 1000 个批量，所以在一个回合里面更新了参数 1000 次
假设有 1000 个数据，批量大小（batch size）和 Sigmoid的个数都是超参数，可以自行设置不同的值。所以做了一个回合的训练其实不知道它更新了几次参数，有可能 1000 次，也有可能 10 次，更新次数取决于它的批量大小。

2、模型变形

其实还可以对模型做更多的变形，不一定要把 Hard Sigmoid 换成 Soft Sigmoid。HardSigmoid 可以看作是两个修正线性单元（Rectified Linear Unit，ReLU）的加总，ReLU 的图像有一个水平的线，走到某个地方有一个转折的点，变成一个斜坡，其对应的公式为： $c\ast max\left ( 0,b+wx_{1} \right )$

要合成 i 个 Hard Sigmoid，需要 i 个 Sigmoid，如果 ReLU 要做到一样的事情，则需要 2i 个 ReLU，因为 2 个 ReLU 合起来才是一个 Hard Sigmoid。因此表示一个 Hard 的 Sigmoid 不是只有一种做法。在机器学习里面，Sigmoid 或 ReLU 称为激活函数（activation function）

Sigmoid 或 ReLU 称为神经元（neuron），很多的神经元称为神经网络（neural network）。人脑中就是有很多神经元，很多神经元串起来就是一个神经网络，人工智能就是在模拟人脑。每一排称为一层，称为隐藏层（hiddenlayer），很多的隐藏层就“深”，这套技术便称为深度学习。现在人们把神经网络越叠越多，越叠越深，以降低错误率达到更好的拟合效果，但是在训练拟合的过程中要注意防止过拟合（overfitting）

深度学习的训练会用到反向传播（BackPropagation，BP），其实它就是比较有效率、算梯度的方法。

3、机器学习框架

在机器学习中会有训练数据和测试数据，他们之间最大的差异就是测试集只有 $x$ 没有 $y$ ，数据如下所示：

训练数据： $\left \{ \left ( x^{1},y^{1} \right ),\left ( x^{2},y^{2} \right ),\cdots ,\left ( x^{N},y^{N} \right ) \right \}$ ，测试数据： $\left \{ x^{N+1},x^{N+2},\cdots ,x^{N+M} \right \}$

训练有三个步骤：

先写出一个有未知数 $\theta$ 的函数， $\theta$ 代表一个模型里面所有的未知参数， $f_{\theta }\left ( x \right )$ 的意思就是函数叫 $f_{\theta }\left ( x \right )$ ，输入的特征为 $x$
定义损失，损失是一个输入就是一组参数的函数，然后利用损失去判断这一组参数的好坏
解一个优化的问题，找一个 $\theta$ ，能够让损失的值越小越好。让损失的值最小的 $\theta$ 为 $\theta ^{\ast }$ ，即： $\theta ^{\ast }=\arg _{\theta }min L$

有了 $\theta ^{\ast }$ 以后，就把它拿来用在测试集上，也就是把 $\theta ^{\ast }$ 带入这些未知的参数，本来 $f_{\theta }\left ( x \right )$ 里面有一些未知的参数，现在 $\theta$ 用 $\theta ^{\ast }$ 来取代，输入是测试集，输出的结果存起来，上传到Kaggle 即可。

hahaha都看到这里了，要是觉得有用的话就辛苦动动小手点个赞吧！