CodeTON Round 8 div2 A-C题解

A. Farmer John’s Challenge

题意：

题目链接：https://codeforces.com/contest/1942/problem/A
题解：考虑有序数组中把a1移到最后去，如果此时还想是排序状态的话a1一定大于等于an，然而一开始的状态中a1又一定小于等于an，所以如果想要有两个及以上的数组的话a1一定等于an，这样的话a1到an全是一个数，这样排序数组就有n个，倘若a1不等于an，排序状态就有0或1个，所以其实一共就三种情况，分别构造即可。
代码：

#include <iostream>

using namespace std;

int main()
{
    int t;
    cin >> t;
    while(t--) {
        int n,k;
        cin >> n >> k;
        if(n==k) {
            for(int i = 1;i <= n;i++) cout << 1<<" ";
            cout<<endl;
        }
        else if(k==1) {
            for(int i = 1;i <= n;i++) cout << i << " ";
            cout<<endl;
        }
        else cout << -1 << endl;
    }

    return 0;
}

B. Bessie and MEX

题意：

题目链接：https://codeforces.com/contest/1942/problem/B
题解：由a数组构造p数组，由题p[i]=mex(p[1]…p[i])-a[i]，看上去情况很多，但是有一个p值是可以确定的，那就是p[n]=mex(p[1]…p[n])-a[n]=n-a[i]，那么p[n]确定了再往前看p[n-1]可以确定吗？是可以的，因为此时的mex值就是p[n]的值，那么p[n-2]呢？此时mex值是p[n]与p[n-1]中的最小值，由此，每一个p值都可以由后面的p的最小值和a数组唯一确定下来，然后p数组就构造出来了。
代码：

#include <iostream>
#include<vector>
using namespace std;
const int N = 2e5+7;
int a[N];
int main()
{
    int t;
    cin >> t;
    while(t--) {
        int n;
        cin >> n;
        for(int i = 1;i <= n;i++) cin >> a[i];
        int p = n;
        vector<int> ans;
        int mins = n;
        for(int i = n;i >= 1;i--) {
            ans.push_back(mins-a[i]);
            mins = min(mins,mins - a[i]);
        }
        for(int i = ans.size()-1;i>=0;i--) {
            cout << ans[i] << " ";
        }
        cout << endl;
    }

    return 0;
}

C1. Bessie’s Birthday Cake (Easy Version)

题意：

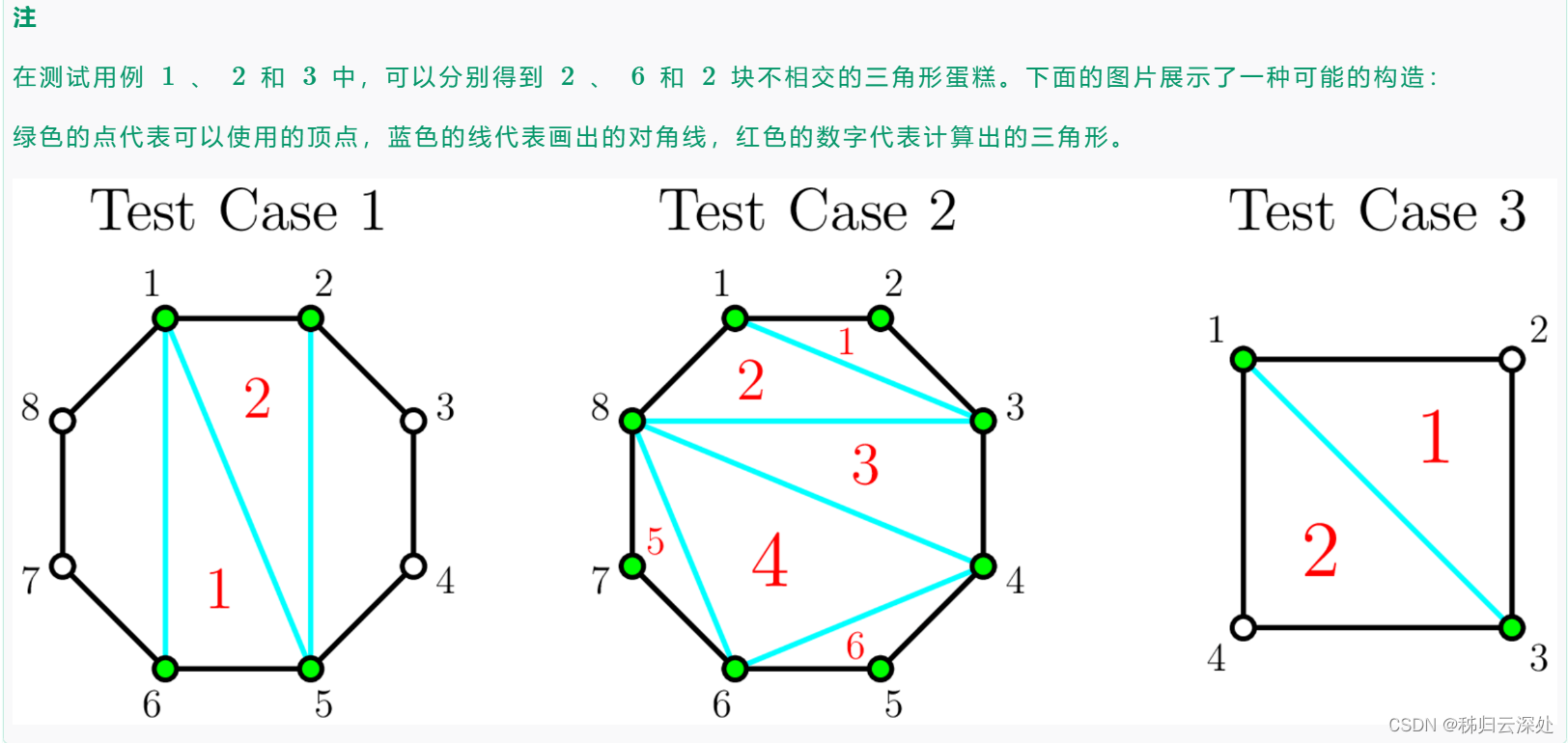
简单来说就是n边形选x个点可以构成多少个三角形。
题目链接：https://codeforces.com/contest/1942/problem/C1
题解：我们可以先将贝西选的x个点排个序，然后我们会发现，将这x个点构成x边形，这个图形内有多少个三角形是固定的，那就是x-2，那么这个x边形之外的呢？画一下会发现，如果两个点之间间隔一个点，那么会贡献一个三角形，所以最后的答案就是x-2+x边形外贡献的三角形。
代码：

#include <iostream>
#include<algorithm>
using namespace std;
const int N = 2e5+7;
int a[N];
int main()
{
    ios::sync_with_stdio(0);
    cin.tie(0);
    cout.tie(0);
 
    int t;
    cin >> t;
    while(t--) {
        int n,x,y;
        cin >> n >> x >> y;
        for(int i = 1;i <= x;i++) cin >> a[i];
        sort(a+1,a+1+x);
        int ans = 0;
        for(int i = 2;i <= x;i++) {
            if(a[i]-a[i-1]==2) ans++;
        }
        if((a[x]+2)%n==a[1])ans++;
        if(x>=3) ans += x - 2;
        cout << ans << endl;
    }
    return 0;
}

C2. Bessie’s Birthday Cake (Hard Version)

题意：


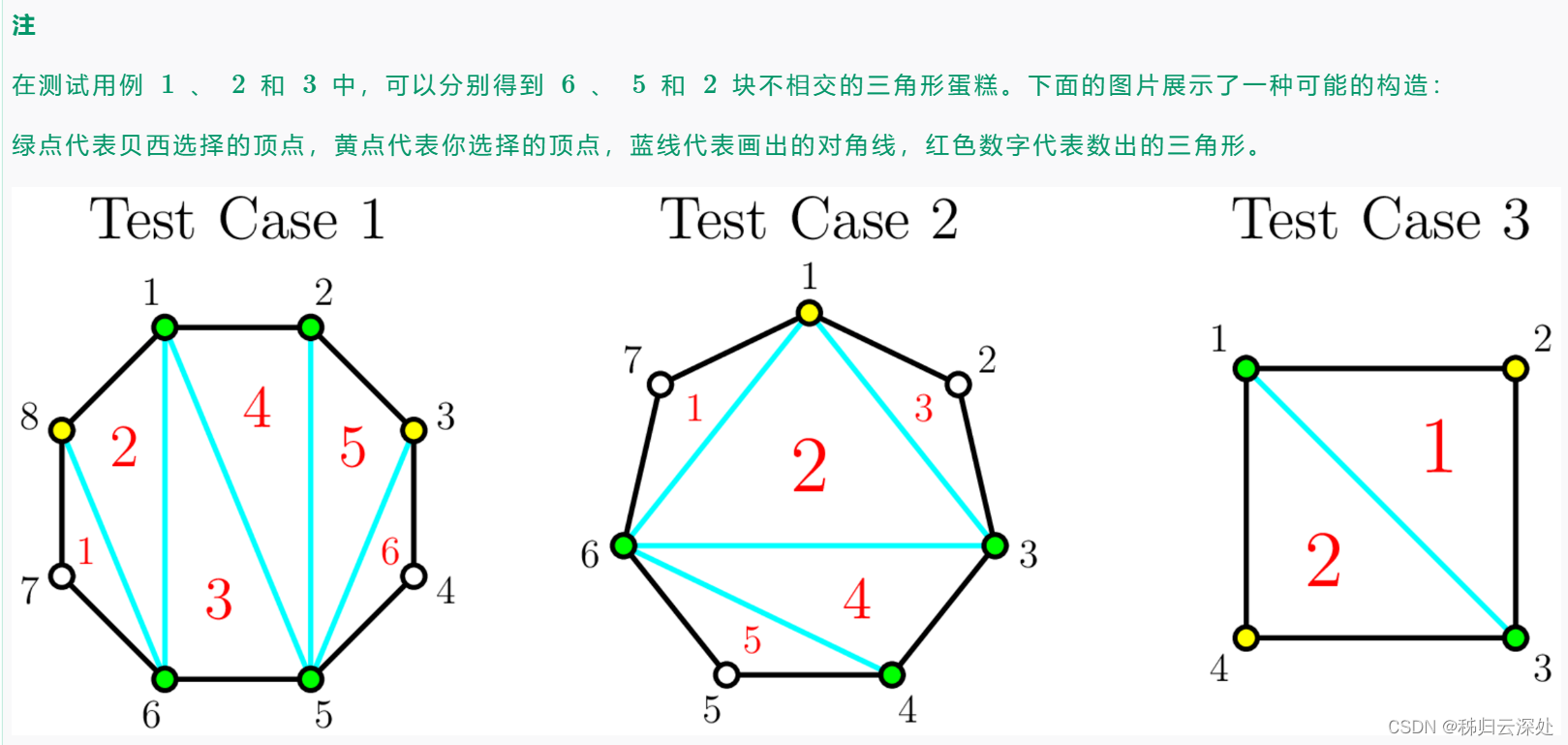
题目链接：https://codeforces.com/contest/1942/problem/C2
题解：考场上我想的是模拟把y个点选出来然后跑一下有多少个三角形就行了，后来发现这种做法不仅找不到答案而且会超时。同第一题，我们还是可以将x个点拍个序，然后思考两个点之间间隔点的数量对答案的贡献，可以发现:1.假如间隔点数量为偶数n，那么可以选n/2个点，每个点对答案的贡献是2（额外的三角形1个加构成的x+1边形会多一个）;2.假如间隔点数量为奇数n，那么还是可以选n/2个点，每个点还是对答案贡献为2但是有一个点很特别就是这n/2个点中的中间点，参考样例2，这个点既可以和左边的点构成额外的一个三角形也可以和右边的点构成一个额外的，所以这个点对答案的贡献为3。也就是说，奇数间隔点区间比偶数间隔点区间会多1的贡献。那么我们先找一遍奇数区间再找一遍偶数区间，这样就可以了吗？还差一点：选点是有限制y的，所以我们应该在这个限制下选更多的奇数区间，所以我们需要对奇数区间排个序，这样可以得到最多的贡献。
代码：

#include <iostream>
#include<algorithm>
#include<cstring>
#include<vector>
using namespace std;
const int N = 2e5+7;
int a[N];
int main()
{
    ios::sync_with_stdio(0);
    cin.tie(0);
    cout.tie(0);
 
    int t;
    cin >> t;
    while(t--) {
        int n,x,y;
        cin >> n >> x >> y;
        for(int i = 1;i <= x;i++) {cin >> a[i];}
        sort(a+1,a+1+x);
        a[x+1] = a[1] + n;
        int ans = 0;
        for(int i = 2;i <= x+1;i++) {
            if(a[i]-a[i-1]==2) ans++;
        }
        ans += x - 2;
        vector<int> v;
        for(int i = 2;i <= x+1;i++) {
            if(a[i]-a[i-1]>2) v.push_back(a[i]-a[i-1]-1);
        }
        sort(v.begin(),v.end());
        for(int u:v) {
            if(y&&(u%2==1)) {
                int ci = min(y,u/2);
                ans += 2*ci;
                if(ci==u/2) ans++;
                y-=ci;
            }
        }
        for(int u:v) {
            if(y&&(u%2==0)) {
                int ci = min(y,u/2);
                ans += 2*ci;
                y-=ci;
            }
        }
        cout << ans << endl;
    }
    return 0;
}