整数的全排列

工具：DEV C++

---

整数的全排列也就是说：

2的全排列是：[1,2],[2,1]

3的全排列是：[1,2,3],[1,3,2],[2,1,3],[2,3,1],[3,1,2],[3,2,1]

实现整数的全排列可以借鉴二叉树的深度遍历思想 ，如下图所示，该树的深度为4，第一层可以理解为该树完成深度遍历后返回的结果，后面的三层可以类比抛硬币求概率的知识来理解。举例子：第二层第一个值为1，第三层第一个值为2,组合[1,2]，第四层第一个值为3，组合[1,2,3]。到达尽头，返回第三层，由于第三层中[1,2]已经遍历过了，故返回到第二层的第二个值为3，组合[1,3]作为第三层，由于[1]的概率已经计算过了，故只需计算[2]的概率，组合[1,3,2]作为第四层。最后不断返回，直到第一层，遍历完[1]后才会开始[2]的遍历，后面以此类推。

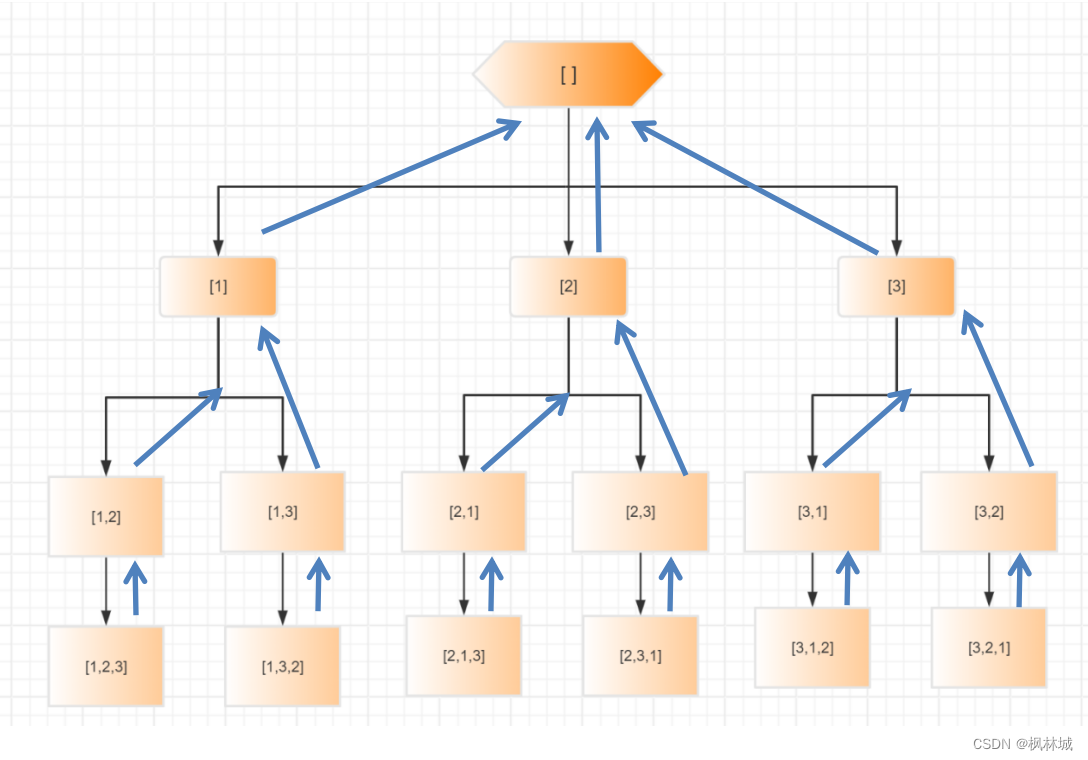
上述的"返回" ,也叫"回溯"。可以使用回溯来实现整数的全排列。

代码如下：

#include<stdio.h>
int arr[10];
bool b[10]={0};          //判断元素是否被使用过
void f(int i,int n){
	if(i==n){            //如果遍历的元素值与最大的值相等，则输出结果
	for(int k=0;k<n;k++){
		printf(" ");
		printf("%d",arr[k]);
	}
	printf("\n");
	return;
  }else{
    for(int k=1;k<=n;k++){
  		if(b[k])continue;          //使用过的元素，选择跳过
  		arr[i]=k;                  //存入数组
  		b[k]=true;                //记录使用过的元素值
  		f(i+1,n);                 //递归实现n个元素(1,2,3...n)之间的组合
  		b[k]=false;              //使用完毕，恢复初始状态，下一次继续使用
	}
  }
}
int main(){
int n;
scanf("%d",&n);
f(0,n);
return 0;	
}

感谢大家观看 ！