【数据结构】线性表的链式存储

🎇[数据结构]线性表——链式存储🎇

---

 

🌟 正式开始学习数据结构啦~此专栏作为学习过程中的记录🌟

---

🚀线性表的顺序存储导航💎：👉[数据结构]线性表——顺序存储👈

🍰1.引言

在之前的学习中我们了解到：

①对于顺序存储

优点：可以随机访问元素，因为可以通过下标直接访问特定位置上的元素，其地址也可以用公式直接表示

缺点：
1. 插入和删除需要移动大量元素
2. 不易改变数组的容量（需要动态申请内存）

所以针对顺序存储的缺点，我们可以进行优化，也就得到了链式存储结构，它通过链建立起数据元素之间的逻辑关系

②对于链式存储

优点：
1. 不需要连续的存储单元，在逻辑上相邻的元素，不要求在物理上也相邻
2. 插入和删除不需要移动元素，只需要修改指针

缺点：
1. 失去顺序存储可随机访问元素的优点（访问元素需要遍历）
2. 存储链表指针需要消耗一定的存储空间

可以看到，顺序表的链表的优缺点是互补的，但我们往往还是习惯于选择链表这一存储结构

如图所示：

🍰2.单链表

🚀1.了解单链表

什么是单链表？

单链表：指通过一组任意的存储单元来存储线性表中的数据元素，为了建立数据元素之间的线性关系，每个链表结点，除了要存放数据信息之外，还需要存放一个指向后继的指针

单链表的结点结构为：

定义链表结点类型:

typedef struct LNode{ //这里不能省去LNode，因为程序在还未进行别名时就会调用该结构体（定义指针域时）
	Elemtype data;
	struct LNode* next; //这里在命名前调用了结构体数组
}LNode,*Linklist;

注意：
1. 虽然typedef是重命名格式，但仍要先声明结构体名称struct LNode，因为在重命名之前就已经需要调用结构体类型(LNode *)定义成员next
2. 这里(LNode *)和LinkList 都表示结构体指针，而LNode * 强调结点，LinkList强调单链表

头指针：L，用来标识一个单链表，头指针为NULL时表示一个空表

头结点：放在单链表的第一个元素之前，不存放信息，只是起到利于操作的作用（一般不计入表长），头结点的指针域指向线性表的第一个元素

头指针和头结点的区别：
无论有没有头结点，头指针都指向链表的第一个结点；而头结点是带头结点的链表中的第一个结点

带头结点链表的优点：

1. 由于第一个数据结点的位置被存放在头结点的指针域中，因此，在链表的第一个位置上的操作和在表的其他位置的操作一致，无需特殊处理
2. 无论链表是否为空，其头指针都指向头结点，因此，空表和非空表的处理统一

🚀2.单链表的操作

🔆1.初始化和判空（Initlist && Empty）

①不带头结点

不带头结点，头指针初始化指向NULL

1. 初始化一个空链表:

//1.1.不带头结点
bool Initlist(Linklist & L) { //L是一个指针
	L = NULL; //没有头结点，头指针指向NULL
	return true;
}

2. 判空

头指针指向空

bool Empty(Linklist L) {
	if (L == NULL)
		return true;
	else
		return false;
}

②带头结点

带头结点时，头指针指向头结点

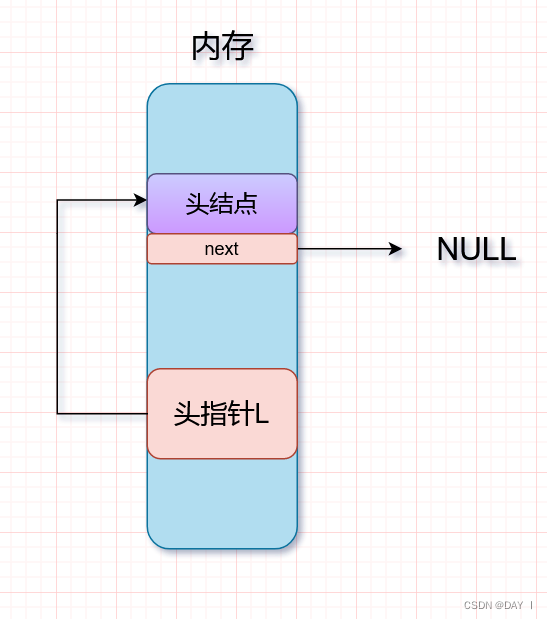
1. 初始化一个空链表:

这里传入的是单链表的头指针，而头指针指向头结点，所以需要为头结点申请一片内存空间

bool Initlist(Linklist& L) { //L是一个指针
	//将起始位置赋值给 L指针
	L = (LNode*)malloc(sizeof(LNode*)); //申请一片内存空间存放头结点，头指针指向头结点（相当于*p=&x一样）
	if (L == NULL)
		return false; //内存不足
	L->next = NULL; //头结点之后还没有结点
	return true;
}

2. 判空

头结点指向空

bool Empty(Linklist L) {
	if (L->next == NULL)
		return true;
	else
		return false;
}

🔆2.查找操作（GetElem）

①按位序查找

在单链表中从第一个结点出发，顺指针next域逐个往下搜索，直到找到第i个结点为止，若未找到，则返回$NULL$，最终得到指向结点 $i$ 的指针 $p$

代码实现：

//默认带头结点（i=0）
LNode* GetElem(Linklist& L, int i) { //得到指向位序为i的元素的指针（即i的前驱）
	if (i < 1)
		return false;
	LNode* p; //指针p指向当前扫描到的结点
	int j = 0; //当前p指向的是第0个结点(头结点)
	p = L; //L指向头结点，头结点是第0个结点（不存数据）
	while (p != NULL && j < i) { //循环找到第i个结点
		p = p->next;
		j++;
	}
	return p; //返回第i个元素
}

查找的时间复杂度为$O(n)$

②按值查找

从单链表的第一个结点开始，由前向后依次比较表中各结点的值，若等于指定的$e$，则返回指向该结点的指针 $p$，否则返回$NULL$

代码实现：

//默认带头结点
LNode* Locateelem(Linklist& L, Elemtype e) {
	LNode* p = L->next;
	while (p != NULL && p->data != e) {
		p = p->next;
	}
	return p; //找到后返回该指针，否则返回NULL
}

🔆3.插入操作（ListInsert）

①按位序插入（带头结点）

插入结点操作将作将值为x的新结点插入到单链表的第i个位置上，先检查插入位置的合法性，然后找到插入位置的前驱结点，即第$i-1$个结点，再在其后插入新结点

这里我们可以用按位查找 找到指向i-1个结点的指针

图解：

我们假设第$i$个结点为$b$，查找得到第$i-1$个结点为$a$，我们令指针$P$指向查找得到的第$i-1$个结点，指针$S$指向新结点，我们依次连接s->next与p->next，实现逻辑上删除原来$a,b$之间的链

//顺序不能交换
s->next=p->next;
p->next=s;

插入结点代码实现：

LNode* Getelem(Linklist& L, int i) { //得到指向位序为i的元素的指针（即i的前驱）
	if (i < 1)
		return false;
	LNode* p; //指针p指向当前扫描到的结点
	int j = 0; //当前p指向的是第0个结点(头结点)
	p = L; //L指向头结点，头结点是第0个结点（不存数据）
	while (p != NULL && j < i) { //循环找到第i个结点
		p = p->next;
		j++;
	}
	return p; //返回第i个元素
}

bool ListInsert(Linklist& L, int i, Elemtype e) { //在位序为i处插入元素e
        //得到i-1的指针
        LNode *p=GetElem(L,i-1);

	//此时，p指向第i-1个结点，s指向新结点
	LNode* s = (LNode*)malloc(sizeof(LNode)); //申请一个新结点
	s->data = e; //结点数据为e

        s->next = p->next;
	p->next = s;

	return true;
}

其时间复杂度来源于位序查找：

插在表头和表尾均不用特判

②按位序插入（不带头结点）

当不带头结点时，头指针L指向第一个结点（不是头结点），因此需要特判，其他操作同带头结点的一致

代码实现：

bool ListInsert(Linklist& L, int i, int e) {
	if (i < 1)
		return false;
	if (i == 1) { //这里i等于1时要特判，因为没有头结点了 头指针直接指向的是第一个数据
		LNode* s;
		s = (LNode*)malloc(sizeof(LNode)); //申请一个新结点
		s->data = e;
		s->next = L;
		L = s;
		return true;
	}
	LNode* p; //指针p指向当前扫描到的结点
	int j = 1; //当前p指向的是第1个结点（没有头结点了，所以从第一个元素结点开始）
	p = L; //头指针指向第一个结点
	while (p != NULL && j < i - 1) { //循环找到第i-1个结点
		p = p->next;
		j++;
	}

        //后续操作一致
	if (p == NULL)
		return false;
	LNode* s = (LNode*)malloc(sizeof(LNode));

	s->data = e;
	s->next = p->next;
	p->next = s;

	return true;
}

③后插操作

后插，即为在指定的某个点之后插入一个新结点

1. 先遍历找到指向指定点的指针$P$，根据单链表的单向性，我们可以很轻易地找到$P$指针指向结点的下一个结点
2. 开辟一个新结点，用指针$S$指向新结点，之后实现逻辑上的插入

代码实现;

bool InsertNextNode(LNode *p,Elemtype e) {
	if (p == NULL)
		return false;
	LNode* s = (LNode*)malloc(sizeof(LNode));
	if (s == NULL)
		return false; //分配内存空间失败
	s->data = e;
	s->next = p->next;
	p->next = s;
	return true;
}

所以，其实之前做的按位序插入也是一种后插操作，那这里可能就有疑惑了，明明是在第i个位置上插入新元素，原本元素向后移动，应该是前插呀？其实并不是，逻辑上是前插，但其实我们是在得到第$i-1$个结点之后，在第$i-1$个元素后面进行后插操作的

那么，能不能进行前插操作呢？

④前插操作

前插，即在指定结点之前插入新结点

由于单链表只能从前向后扫描，而无法从后往前查找，因此，我们无法通过一个结点找到它前面的结点

对第i个元素实现前插新元素e的操作：

1. 按位序插入：通过GetElem(L,i-1)找到指向第i-1个元素的指针，对第$i-1$个元素进行后插，时间复杂度为$O(n)$

有没有好的方法呢？

2. 偷天换日法：要在第i个结点前插入新结点s，我们无法移动指向第i个结点的指针，但我们可以移动结点中的数据，时间复杂度为$O(1)$

我们对结点i进行后插操作，加入新结点e，不改变位置，交换两个结点对应的元素值，则实现了前插操作

改指针+改数据：

//逻辑代码
s->next = p->next;
p->next = s;
s->data = p->data;
p->data = e;

图解：

↓

完整代码实现：

bool InsertPriorNode(LNode* p, Elemtype e) {
	if (p == NULL)
		return false;
	LNode* s = (LNode*)malloc(sizeof(LNode));
	if (s == NULL)
		return false;
	s->next = p->next;
	p->next = s;
	s->data = p->data;
	p->data = e;
	return true;
}

🔆4.删除操作（DeleteNode）

①按位序删除

即将单链表的第i个结点删除：

先检查位置的合法性，再查找表中第$i-1$个结点，即被删除结点的前驱结点，实现逻辑上连接后，再将其删除

代码片段：

p=GetElem(L,i-1);
p->next=q->next;
free(q);

完整代码实现：

bool DeleteNode(Linklist &L,LNode* q,int i,Elemtype &e){ //删除q的元素
	LNode *p = Getelem(L, i-1);//得到i的前驱i-1
	e = q->data; //记录删除结点的值
	q = p->next;
	p->next = q->next;
	free(q); //释放结点的存储空间
}

②删除指定结点 $\ast p$：

和之前前插操作一样，由于我们无法得到结点$\ast p$ 的前驱结点，因此，要删除指定结点也同样有两种方式：

1. 按位序删除：从前往后遍历得到$\ast p$ 的前驱结点，时间复杂度为$O(n)$

2. 偷天换日法：删除指定结点可以通过删除$\ast p$ 结点的后继实现，实质就是将其后继结点的值赋予$\ast p$，再删除其后继结点，时间复杂度为$O(1)$

p不动，删q

//逻辑代码
q=p->next;
p->data=q->data;
p->next=q->next;
free(q);

图解：

↓

完整代码实现：

bool DeleteNode(LNode* p) { //删除指针p指向的结点
	if (p == NULL)
		return false;
	LNode* q = p->next; //因为不知道p的前驱，只能找后继
	p->data = q->data; //值传递
	p->next = q->next; //指针传递
	free(q); //释放结点
	return true;
}

🔆5.求表长（length）

求表长就是遍历整个链表，直到指向NULL为止

要注意的是，头结点是不算入链表长度中的

int length(Linklist &L) {
	int len = 0;
	LNode* p = L;
	while (p->next != NULL) {
		p = p->next;
		len++;
	}
	return len;
}

🔆6.单链表的建立(GetList)

①尾插法建立单链表

即新结点加入在当前链表的表尾，其次序和输入的顺序一致

由于每次加入到表尾时，我们都需要用到表尾指针进行后插操作，所以，我们可以增加一个尾指针 $r$，始终指向表尾结点

不断开辟结点+尾插

完整代码实现：

Linklist List_Tailinsert(Linklist& L) {
	int x;
	L = (Linklist)malloc(sizeof(LNode));
	LNode* s, * r = L; //s为结点指针 r为尾指针
	scanf("%d", &x);
	while (x != 9999) { //x=9999为结束标志
		s = (LNode*)malloc(sizeof(LNode));
		s->data = x;
		r->next = s; //连接
		r = s; //移动尾指针
		scanf("%d", &x);
	}
	r->next = NULL;
	return L;
}

②前插法建立单链表

即不断将新结点插入到链表的表头

注意：头插法建立得到的是输入的逆序版本

完整代码实现：

Linklist List_Headinsert(Linklist& L) {
	LNode *s;
	int x;
	L = (Linklist)malloc(sizeof(LNode));
	L->next = NULL; //要提前初始化NULL，因为结束时不会再遍历一次补上这个NULL
	scanf("%d", &x);
	while (x != 9999) {
		s = (LNode*)malloc(sizeof(LNode));
		s->data = x;
		s->next = L->next; //前驱一直是头结点
		L->next = s;
		scanf("%d", &x);
	}
	return L;
}

🍰3.双链表

🚀1. 了解双链表

为什么需要双链表？

单链表缺陷：只能从头结点依次顺序地向后遍历，要访问某个结点的前驱结点不方便

双链表改进：加入了指针$prior和next$，分别指向了前驱结点和后继结点，可以很方便地找到前驱结点

定义双链表结点：

由于每一个双链表结点都需要存放两个指针，所以存储密度较单链表低

typedef struct DNode{
    int data;
    struct DNode *prior,*next;
}DNode,*DLinkList;

🚀2. 双链表的操作

🔆1. 双链表的插入操作

在双链表中p指向的结点之后插入结点$\ast s$

s->next=p->next;
p->next->prior=s;
s->prior=p;
p->next=s;

可以看到，这里是先连接了s与后一个结点之间的两条链，再连接p与s之间的两条链的，如果不注意顺序，容易出现指针指向自身的情况

这里还要注意：当在双链表的尾部插入结点时（p->next=NULL），要特判：
此时，NULL不会指向s结点，所以应该是单向的（也就是不存在步骤②）

完整代码实现：

bool InsertNextDNode(DNode* p, DNode *s) {
	if (p == NULL || s == NULL) {
		return false;
	}
	s->next = p->next; //若都不为空，s的后继一定存在
	if (p->next != NULL)
		p->next->prior = s; // 若后继不为空，则一定为双向的
	s->prior = p;
	p->next = s;
	return true;
}

🔆2. 双链表的删除操作

删除双链表中结点$\ast p$ 的后继结点$\ast q$

p->next=q->next;
q->next->prior=p;
free(q);

其删除顺序为：

同样地，当删除结点为尾结点时，也需要特判，即没有操作②

完整代码实现：

bool DeleteNextDNode(DNode* p) {
	if (p == NULL)
		return false;
	DNode* q = p->next; //定义p的后继
	if (q == NULL)
		return false;
	p->next = q->next;
	if (q->next != NULL)
		q->next->prior = p;
	free(q);
	return true;
}

🍰4.循环链表

🚀1. 循环单链表

循环单链表和单链表的区别在于，表中的最后一个结点不是$NULL$，而是指向头结点，从而使整个链表形成一个环

特点：
在循环单链表中，表尾结点$\ast r$的next域指向$L$，故表中没有指针域为$NULL$的结点，因此，循环单链表为空表的条件不是头结点指向NULL，而是头结点等于头指针$L$

①初始化：

循环列表初始化，让头结点的next指针等于头指针$L$

代码实现：

bool InitList(Linklist& L){
	L = (LNode*)malloc(sizeof(LNode));
	if (L == NULL)
		return false;
	L->next = L;
	return true;
}

②判空：

bool Empty(Linklist& L) {
	if (L->next == L)
		return true;
	return false;
}

循环单链表小结：

1. 循环单链表在任何一个位置上的插入和删除操作都是等价的，无需特判是否是表尾；也可以从表中的任意一个结点开始遍历整个链表
2. 对循环单链表可以不设头指针而仅设尾指针，从而使得操作效率更高
   其原因是，若设的是头指针，对表尾进行行操作需要O(n)的时间复杂度，而若设的是尾指针 r, r->next即为头指针，对表头与表尾进行操作都只需要O(1)的时间复杂度
   

ഒ实战演练ഒ：

🔱思路分析：

1. 对于一个空循环单链表，有head->next=head，推理得（head->next）->next=head，因此，可能是一个空表；
2. 对于含有一个元素的循环单链表来说，头结点的next指针指向第一个结点，而第一个结点的next指针指向头结点=head，所以也可能只含有一个结点

图解：

🚀2. 循环双链表

和循环单链表类似，循环双链表也去除了指向$NULL$的设定，其尾结点的$next$指针指向头结点，头结点的$prior$指针指向尾结点

🔆1. 初始化

让头结点的$prior$指针和$next$指针都等于头指针$L$

代码实现：

bool InitList(DLinklist& L) {
	L = (DNode*)malloc(sizeof(DNode));
	if (L == NULL)
		return false;
	L->prior = L;
	L->next = L;
	return true;
}

🔆2. 判空

bool Empty(DLinklist& L) {
	if (L->next == L)
		return true;
	return false;
}

🔆3. 判断p结点是否为尾节点

bool isTail(DLinklist& L, DNode* p) {
	if (p->next == L)
		return true;
	return false;
}

🔆4. 循环双链表的插入

对于循环双链表的插入，对于链表上的每一个结点来说操作一致，无需特判

将结点s插入到$\ast p$后：

bool InsertNextDNode(DNode* p, DNode* s) {
	s->next = p->next;
	p->next->prior = s;
	p->next = s;
	s->prior = p;
}

🔆5. 循环双链表的删除

p->next=q->next;
q->next->prior=p;
free(q);

🍰5. 静态链表

🚀1. 了解静态链表

静态链表借助数组来描述线性表的链式存储结构，结点也有数据域$data$和指针域$next$，不同的是，这里的指针是结点的数组下标，也称为游标

和顺序表一样，静态链表也需要分配一块连续的存储空间，静态链表的首地址存放的是头结点（为0号位置）

定义一个结构体数组:

typedef struct SNode {
	int data;
	int cur;
}SLinklist[Maxsize];

这里SLinklist相当于定义了一个长度为Maxsize的SNode型数组

实例化为：SLinklist a;

SLinklist a=struct SNode a[Maxsize]

游标： 即下一结点所对应的数组中的下标索引值

1. 以-1表示链表结尾
2. 当已开辟的连续的内存空间中，存在未被赋值的内存空间时，其游标标记为-2

🚀2. 静态链表的操作

🔆1. 初始化：

只用将未被赋值的结点对应的游标标记为-2即可

void InitList(SLinklist& a) {
	for (int i = 0; i < Maxsize; i++)
		a[i].cur = -2;
}

🔆2. 判空 & 判满

1. 对于判空：即当头结点（0号位置）对应的游标为-1时，为空表
2. 对于判满：即扫描整个静态链表，若长度为Maxsize-1，则满

   也可以用开辟的数组内存空间全部被占满，不存在游标为-2的单元进行判断

//1. 判空
bool Empty(SLinklist& a) {
	if (a[0].cur == -1)
		return true;
	return false;
}

//2. 判满
bool Over(SLinklist& a) {
	int i = 0,len=0;
	while (i != -1) {
		i = a[i].cur;
		len++;
	}
	if (len == Maxsize-1)
		return true;
	else
		return false;
}

🔆3. 求静态数组的长度

类似地，也是进行扫描，直到遇到终止符-1

int length(SLinklist& a) {
	int j = 0,len=0;
	while (j != -1) {
		j = a[j].cur;
		len++;
	}
	return len;
}

🔆4. 查找操作

1. 按值查找

查找值为$e$的元素，返回它的数组下标

int Findindex(SLinklist& a, int e) {
	int res = 0;
	while (res != -1) {
		int index = a[res].cur; //找到下一个结点
		if (a[index].data == e)
			return index;
		res = index; //让res移动到index的位置，继续搜索
	}
	return -1; //表示不存在
}

2. 按位查找

找到位序为 $i$ 的元素 $e_i$ 对应的数组下标

int Getindex(SLinklist& a, int i) {
	int res = 0,j=0;
	while (res != -1) {
		res = a[res].cur; //得到位序为j得到元素的下标
		j++;
		if (j == i)
			return res;
	}
	return -1; //表示不存在
}

🔆5. 插入操作

要在位序为$i$的位置上插入新元素$e$

同链表类似，只是这里要通过修改游标来实现结点间的逻辑关系

step:

1. 找前驱：找到$a_i$的前驱元素对应的数组下标 $p=index(i-1)$
2. 找空位：扫描整个数组，看是否有空位可以存放新结点e，得到新结点的数组下标 $s$
3. 插入元素：将$s$对应的游标指向$p$的游标（即原来的第$i$个元素），再将$p$对应的游标指向$s$

图解：

假设我们要在第3个位置插入元素4

静态数组：

链表：

代码实现：

bool Insert(SLinklist& a, int i,int e) { //插入位序为i的新元素e
	//1.找前驱
	int p=Getindex(a, i - 1);

	//2.找空位
	int s; //新元素要插入的数组下标
	if (Over(a) || i>length(a)) //如果范围错误
		return false;
	for (int j = 1; j < Maxsize; j++) { //头结点不存数据
		if (a[j].cur == -2)
		{
			s = j;
			break;
		}
	}

	//3.插元素
	a[s].data = e;
	a[s].cur = a[p].cur;
	a[p].cur = s;

	return true;
}

🔆6. 删除操作

若要删除第i个结点（$a_i$）

step:

1. 找下标：得到 $a_{i-1}$ 和 $a_i$ 的数组下标 $p和s$
2. 删元素：将p对应的游标赋值为$a_{i+1}$元素对应的数组下标，再将s对应的游标设置为-2（逻辑上表示该位置为空位）

代码实现：

bool Delete(SLinklist& a, int i) {
	//1.找前驱
	int p = Getindex(a, i - 1); //第i-1个结点的下标
	int s = Getindex(a, i); //第i个结点的下标

	//2.删除
	if (Empty(a) || i > length(a)) //如果范围错误
		return false;

	a[p].cur = a[s].cur; //修改游标：逻辑上移除
	a[s].cur = -2; //在静态链表中设为空位

	return true;
}

---

完整代码实现：

#include<iostream>
#include<stdlib.h>
#define Maxsize 50
using namespace std;

typedef struct SNode {
	int data;
	int cur;
}SLinklist[Maxsize]; //定义一个结构体数组

//初始化
void InitList(SLinklist& a) {
	for (int i = 0; i < Maxsize; i++)
		a[i].cur = -2;
}

//赋值
void GetList(SLinklist& a,int L) {
	int x,index,prior=0,i=0;
	cout << "输入要加入的元素和位置(>=1 && <Maxsize)" << endl;
	while (cin >> x >> index) {
		a[prior].cur = index; //处理前一个结点的游标（初始为头结点）
		a[index].data = x; //处理当前结点的数据域
		prior = index; //改变prior的值，准备进行下一次输入
		i++;
		if (i == L) {
			a[index].cur = -1; //当为最后一个结点时，标记为-1，并退出
			break;
		}
	}
}

//按值查找
int Findindex(SLinklist& a, int e) {
	int res = 0;
	while (res != -1) {
		int index = a[res].cur; //找到下一个结点
		if (a[index].data == e)
			return index;
		res = index; //让res移动到index的位置，继续搜索
	}
	return -1; //表示不存在
}

//按位查找(第i个元素的位置)
int Getindex(SLinklist& a, int i) { //找到位序为i的元素的数组下标
	int res = 0,j=0;
	while (res != -1) {
		res = a[res].cur; //得到位序为j得到元素的下标
		j++;
		if (j == i)
			return res;
	}
	return -1; //表示不存在
}

//判空
bool Empty(SLinklist& a) {
	if (a[0].cur == -1)
		return true;
	return false;
}

//判满
bool Over(SLinklist& a) {
	int i = 0,len=0;
	while (i != -1) {
		i = a[i].cur;
		len++;
	}
	if (len == Maxsize)
		return true;
	else
		return false;
}

//求静态数组长度
int length(SLinklist& a) {
	int j = 0,len=0;
	while (j != -1) {
		j = a[j].cur;
		len++;
	}
	return len;
}

//插入操作
bool Insert(SLinklist& a, int i,int e) { //插入位序为i的新元素e
	//1.找前驱
	int p=Getindex(a, i - 1);

	//2.找空位
	int s; //新元素要插入的数组下标
	if (Over(a) || i>length(a)) //如果范围错误
		return false;
	for (int j = 1; j < Maxsize; j++) { //头结点不存数据
		if (a[j].cur == -2)
		{
			s = j;
			break;
		}
	}

	//3.插元素
	a[s].data = e;
	a[s].cur = a[p].cur;
	a[p].cur = s;

	return true;
}


//删除操作
bool Delete(SLinklist& a, int i) { //删除第i个结点
	//1.找前驱
	int p = Getindex(a, i - 1); //第i-1个结点的下标
	int s = Getindex(a, i); //第i个结点的下标

	//2.删除
	if (Empty(a) || i > length(a)) //如果范围错误
		return false;

	a[p].cur = a[s].cur; //修改游标：逻辑上移除
	a[s].cur = -2; //在静态链表中设为空位

	return true;
}

//打印静态数组
void Print(SLinklist& a) {
	int i = a[0].cur;
	cout << "当前静态链表为：" << endl;
	while (i != -1) {
		cout << a[i].data << " ";
		i = a[i].cur;
	}cout << endl;
}

int main() {
	SLinklist a; //实例化
	InitList(a);

	//1. 赋值静态数组
	int L;
	cout << "请输入初始要加入元素的长度" << endl;
	cin >> L;
	GetList(a, L);

	//2. 打印原始静态链表
	Print(a);

	//3. 查找
	cout <<"值为3的结点对应的数组的下标是（-1表示不存在）：\n" << Findindex(a, 3) << endl;
	cout << "第2个结点对应的数组标为（-1表示不存在）：\n" << Getindex(a,2) << endl;

	//4. 插入操作
	if (Insert(a, 3, 4))
		Print(a); //成功，打印插入后的数组
	else
		cout << "插入失败" << endl;

	//5. 删除操作
	if (Delete(a, 3))
		Print(a);
	else
		cout << "删除失败" << endl;

	system("pause");
	return 0;
}

输出结果：

---

 

🎇本节详细讲解了线性表非常重要的一种存储结构——链式存储，那么线性表的知识就到此结束啦~🎇

如有错误，欢迎指正~！