【算法】—DFS深度优先搜索详解

DFS深度优先搜索

一.引入：深度优先搜索（DFS）

1.dfs引入

💡dfs：一种用于遍历或搜索树或图的算法，沿着树的深度遍历树的节点，尽可能深的搜索树的分支，当节点v的所在边都己被探寻过或者在搜寻时结点不满足条件，搜索将回溯到发现节点v的那条边的起始节点，整个进程反复进行直到所有路径都已经被搜寻，属于盲目搜索,最糟糕的情况算法时间复杂度为O(n！)

也就是说，深度优先搜索会沿着一条路径不断往下搜索直到不能再继续为止，然后再折返，开始搜索下一条候补路径

引例：用迷宫初步理解dfs

如图，假设我们身处在一个迷宫之中，没有标记，没有特殊信号，每一条路都一模一样，当无法用上帝视角去查看迷宫时，我们只能选择盲目地去尝试可能的每一条路径，虽复杂，但却有效：

但要想不重复又不遗漏地尝试所有地路径直到找到终点也不是一件易事，其实，我们可以选择一种特殊的方式探索：从起点开始，贴着其中一边的墙壁，一直沿着该墙面行走，即可找到终点

路径即为上图所示（一直靠着右边墙面行走），那这和dfs有什么关联呢？

其实，这种寻找路径的方式即为dfs，我们可以看到，当面对一个岔路时，以这种方式前进，我们自动选择了其中的一条路径先走（此时路径选择的优先级为右→中→左），直到在该路径下走到死路，我们将顺着墙壁回到上一个岔路口，再选择下一条路径，不断重复直到找到终点

每走到一次死路，其实就是dfs得到的一条路径

由此总结深度优先搜索：

💡从根节点开始，尽可能深的搜索每一个分支，把一个分支的结果搜索完，再去看另一个分支，形象来说就是：“一条路走到底，不撞南墙不回头”

2.dfs的实现方式

①在图中寻找可行路径：

我们现在到图中看dfs的实现步骤：

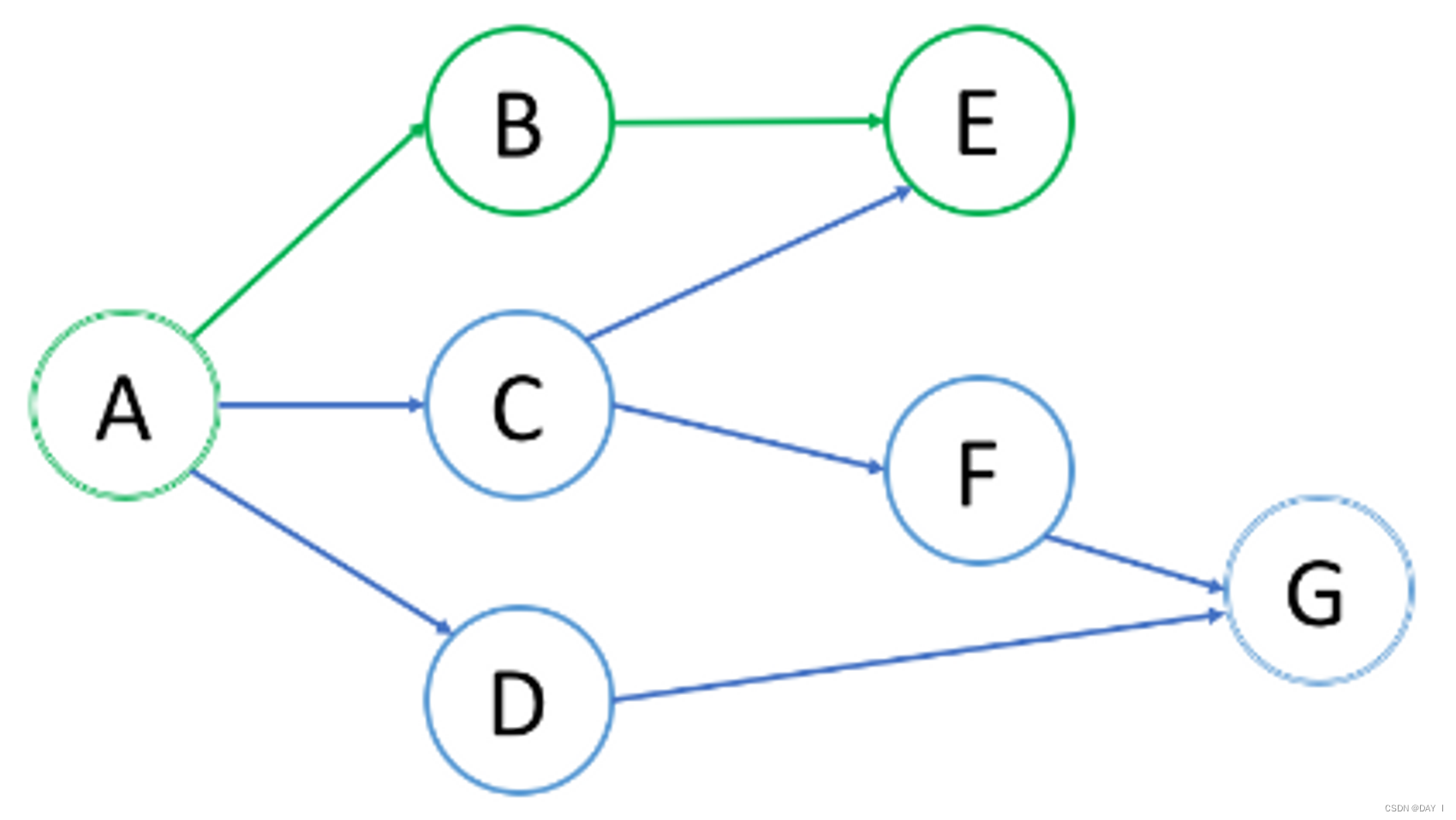
如图，现在我们要找到从A节点到G节点的路径，DFS步骤如下：

1. 从根节点A开始，选择节点B的路径，并回溯，直到到达节点E，无法再深入
2. 接下来回溯到A，选择节点C的路径，先选择E节点，不满足，回溯到C节点
3. 选择下一个未被访问的节点F，不断深入，最终到达G节点
4. 这样，我们就找到了一个A节点到G节点的路径为：A→C→F→G
5. 再次回溯，到A点，这次选择节点D，不断深入，又到达G点
6. 因此，我们再次找到一个A到G的路径为：A→D→G

②dfs与递归：

引论：求解斐波那契数列第20项

斐波那契数列的定义：F(0) = 1, F(1) = 1, F(n) = F(n - 1) + F(n - 2) (n≥2)

1. 递推：

   由斐波那契数列的递推式：f(n)=f(n-1)+f(n-2)

   fib=[0]*22
   fib[1]=1
   fib[2]=1
   for i in range(3,21):
   	fib[i]=fib[i-1]+fib[i-2]
   print(fib[20])
   

2. 递归：

   递归过程为：

   fib(20)=fib(19)+fib(18)

   fib(19)=fib(18)+fib(17)

   …

   fib(2)=fib(1)+fib(0)

def fib(n):
    global cnt
    cnt+=1
    if n==1 or n==2:
        return 1
    return fib(n-1)+fib(n-2)

cnt=0
print(fib(20)) # 6765
print(cnt) # 递归了13529次

💡 递归如此低效的原因：在不断进行着重复的递归调用

改进：记忆化

递归过程中做了很多重复的工作，例如不断地计算fib(3),fib(2),fib(1)，不仅如此，还要连同fib(3)以下的所有fib值一起再计算一遍，其实只用计算一次就够了

为避递归中的重复计算，可以在子问题解决时，保存其结果，再次计算时只需直接调用其结果即可，这种储存已经解决的子问题的方法叫做记忆化

1. 用记忆化优化的递归实现dfs：

   import sys
   sys.setrecursionlimit(1000000)  # 设置递归深度
   def fib(n):
       global cnt
       cnt+=1
       if n==1 or n==2:
           data[n]=1
           return data[n]
       if data[n]!=0: # 如果计算过了，则直接返回
           return data[n]
       data[n]=fib(n-1)+fib(n-2)
       return data[n]
   
   cnt=0
   data=[0]*305
   print(fib(300)) 
   print(cnt) # 递归了597次
   

dfs思路看斐波那契数列：

1. 将F(n)分为两部分F(n - 1)与F(n - 2)时，就可以把F(n)看做迷宫的岔道口，由它可以到达两个新的关键节点F(n - 1) 和 F(n - 2)，而之后计算F(n - 1)时，又可以把F(n - 1)当作在岔道口F(n)之下的岔道口
2. 既然有岔道口，那么一定有死胡同，很容易想象，当访问到F(0)和F(1)时，就无法向下递归下去，因此F(0)、F(1)在这里就是死胡同，这样说来，递归中的递归式就是岔道口，而递归边界就是死胡同，这样一来，就可以把如何用递归实现深度优先搜索的过程理解的很清楚
3. 递归可以进入到下一个节点，结束完函数操作后，又可以返回到上一个函数节点继续操作，因此，使用递归可以很好地实现深度优先搜索

注意：并不是说深度优先搜索就是递归，只能说深度优先搜索是递归的一种实现方式，因为使用非递归也能实现DFS的思想，但是一般情况下会比递归麻烦。不过，使用递归时，系统会调用一个叫系统栈的东西来存放递归中每一层的状态，因此使用递归来实现DFS的本质其实还是栈

🧐 递归与dfs的不同点：

深搜的递归函数也需要跳出条件，也需要自行调用，区别是深搜在遍历时候递归调用的点，需要返回上一个点时还原上一个的状态，因此这里需要一个“回溯”操作

③dfs模板框架：

💡
剪枝：每到一层就判定一次，若不满足条件，则返回上一层
标记：当元素未被访问过时，我们访问该元素，并进行标记，表示已经访问了
回溯：对该元素深度搜索后，要还原该元素的状态，解除标记，并进行下一轮搜索

判断边界：
相应操作
尝试每一种情况：
if 满足条件：
标记
dfs（下一层递归）
回溯`

import sys
sys.setrecursionlimit(1000000)  # 设置递归深度

ans # 答案 全局变量
def dfs(层数)：
		if 出局条件：  
				更新答案
				return # 返回上一层
		剪枝 # 将重复判断的去除 减小复杂度---一般用if
		for (枚举下一层的情况)： # 对每个情况继续dfs
				if used[i]==0:     # 如果元素i没有被标记过
						used[i]==1     # 标记：保护现场
						对所要变化的元素在当前层赋值
            dfs(层数+1)     # 下一层dfs
						used[i]==0     # 回溯：恢复现场
		return     # 返回上一层

✅ dfs一般为：标记+dfs+回溯 简单来说，回溯就是要消除搜索过程中的不同可能性之间对中间变量的影响 还原此层的状态
便于探索下一可能性 满足则深搜 不满足则回退

二.dfs的典型问题与方法

1.dfs实现排列组合

①自写排列算法：

思路分析：

让数字1~n进行全排列，我们从前往后（自顶向下）考虑：

1. 让第一个数字不同，因为第一个数字的可能情况有n种（1~n），我们可以看作是将第一个数与后面的n-1个数进行交换得到n个不同的情况（也包括不交换的时候），从初始状态1 2 3 4…n开始，即将数字2~n的位置与1进行交换，得到：

   1 2 3 4… n

   2 1 3 4… n

   …

   n 2 3 4… 1

由于第一个数字不同，那么不管后面n-1个数字怎么排，这个数组都不可能相同，有n种

这是递归的第一层

1. 在上面得到的每一个数组中，去掉第一个数字后，对后面的n-1个数字进行类似的排列：

   例如将此时的初始状态定为 2 1 3 4… n，去掉第一个数字2之后，对接下来的n-1个数字进行全排列，和刚刚的思路一致，不断将后面的数字与首位数字进行交换，得到：

   1 3 4… n

   3 1 4… n

   4 3 1… n

   …

   n 3 4… 1

由于当前的首位数字不同，则后面的n-2个数不管怎么排，这个数组都不可能相同，有n-1种

这是递归的第二层，由此下去，最终到n-1层即为第n-1个数只能与最后一个数字进行交换，这时结束递归，即得到n个数的全排列

代码实现：

def dfs(s,t):
		if s==t:   # 递归结束，输出一个全排列
				print(a[:t])
		else:
				for i in range(s,t+1):    # 当前层下排序数组的第一个数字为a[s] 
						a[s],a[i]=a[i],a[s]   # 交换第一个数和后面的数
						dfs(s+1,t)            # 缩小范围
						a[s],a[i]=a[i],a[s]   # 回溯：还原状态

a=[i for i in range(1,10)]
n=int(input())
dfs(0,n) # 表示对前n个数进行全排列

从小到大的全排列：

def dfs(s,t):
  if s==t:   #递归结束，输出一个全排列
    print(b[0:n])
  else:
    for i in range(t):
      if vis[i]==False:
        vis[i]=True
        b[s]=a[i]   # 存排列
        dfs(s+1,t)
        vis[i]=False
              
a=[1,2,3,4,5,6,7,8,9]
b=[0]*10   #记录生成的一个全排列
vis=[False]*10  #记录第 i 个数是否用过
n=3
dfs(0,n)   #前 n 个数的全排列 

简单示例：

全排列

AC代码实现：

class Solution:
		def permute(self, nums: List[int]) -> List[List[int]]:
        def dfs(s,t):
            if s==t:
                res.append(nums[:t])
            for i in range(s,l):
                nums[s],nums[i]=nums[i],nums[s]
                dfs(s+1,t)
                nums[s],nums[i]=nums[i],nums[s]
            return res
        res=[]
        l=len(nums)
        dfs(0,l)
        return res

②自写组合算法

组合其实就是在dfs时，选或不选第k个数，构成了两种情况，分别对其进行dfs，就实现了各种组合

def dfs(k,t):  # 深搜到第k个数
    if k==t:
        for i in range(t):
            if vis[i]==1: # 如果前面层选择了这个数
                print(a[i],end='')
        print()
    else:
        vis[k]=0   # 不选第k个数
        dfs(k+1,t)
        vis[k]=1   # 选第k个数
        dfs(k+1,t)

vis=[0]*10
a=[1,2,3,4,5,6,7,8,9]
n=int(input())
dfs(0,n) # 对前n个数进行组合

③库函数排实现列组合(补充了解)

python中又库函数可以实现排列组合，这里作为补充，实际上，在一些题目中，如果用库函数，往往会超时，它只适用于数字规模较小的情况

1. 排列库函数——permutations

接收一个可迭代对象和 len（需要排列的长度作为输出）： 元素均按位置而不是按值排列

可以用.join()依次从迭代器中取出

from itertools import  permutations
permutations()   
.join()    

具体应用：

1. 对字符串排序

from itertools import  permutations
a = 'abc'       # 对字符串进行permutations排列组合---不同的位置有不同的结果
for i in permutations(a,3):
    x = ''.join(i)    # 表示加入元素
    print (x,end=' ')

b. 对列表排序

1.排列无序
from itertools import  permutations
b = [1,2,3]     # 对列表进行permutations排列组合
for j in permutations(b,3):
    print (''.join('%d'%o for i in j))
2.有序
c=['1','2','3']  # 以字符形式将数字存入列表
for i in permutations(c,3):
    print(''.join(i))

1. 组合库函数——combinations

用法和排列函数类似：

from itertools import combinations
combinations()

x = {'a','b','c','d'} # 对集合进行combinations排列组合
for i in combinations(x,2):
    print (i)

🔥 注意：这里combinations和permutations返回的是对象地址，因为其返回值为iterators（迭代器）,所以想要使用，需要将 iterator 转换成 list

2.dfs的深入应用

①迷宫问题：

迷宫

思路分析：

题目要求找到起点到终点的所有路径，我们可以用dfs进行求解：

1. graph用于存图，将障碍物标记为1，其余为0
2. vis用于判断该点是否走过
3. check函数用于限定不能越界

对于dfs：

我们从起点开始深搜

1. 结束条件：到达终点，路径数+1；
2. 遍历当前点的四个方向，如果可以走，则继续dfs下一个点；
3. 标记与回溯：

🔥 注意：在dfs标记与回溯时，我们应该是标记当前点，即将坐标改变前的点为走过的状态，回溯也是回溯当前点，而不是坐标改变后的点

如果标记改变坐标后的点，那么将会出现这种情况：

...        
if check(nx,ny): # 如果该点满足条件
		vis[x][y]=1
    dfs(nx,ny)
    vis[x][y]=0
...
输入：
5 5 5 
1 2 5 5
2 1
2 2
2 3
2 4
3 4

输出：
20（正确答案为10）

为什么会多出来这些情况呢？

我们来解释一下，当标记改变坐标后的点时，未改变前的点可能未被标记，这会导致什么呢？我们拿案例中的矩阵进行分析：

我们模拟一种此时的dfs走过的路径，我们发现，进入迷宫后，先向左边走去，发现是死胡同之后再回溯到起点，之后走向终点，但其实这条路径是错的！因为它经过了起点两次！为什么会造成这个原因呢？就是因为我们只改变了（1，1）的 vis值，即只标记了（1，1），但没有标记起点（1，2），造成了起点没有被经过的错觉，所以造成了多出的路径

💡 因此，标记与回溯应该标记当前走过的点，而不是即将走的点

代码实现：

def check(a,b):
    if 1<=a<=n and 1<=b<=m and graph[a][b]==0 and vis[a][b]==0:
        return True
    return False

ans=0
def dfs(x,y):
    global ans
    if x==fx and y==fy:
        ans+=1
    for i,j in [(1,0),(-1,0),(0,1),(0,-1)]: # 表示所走的四个方向
        nx=x+i; ny=y+j
        if check(nx,ny): # 如果该点满足条件
            vis[x][y]=1
            dfs(nx,ny)
            vis[x][y]=0

n,m,t=map(int,input().split())
sx,sy,fx,fy=map(int,input().split())
graph=[[0]*(m+1) for i in range(n+1)] # 存图
for _ in range(t):
    zx,zy=map(int,input().split())
    graph[zx][zy]=1 # 1表示障碍

vis=[[0]*(m+1) for i in range(n+1)] # 标记
dfs(sx,sy)
print(ans)

②寒假作业

寒假作业

思路分析：

题目要求在1~13之间选12个不同的数字填入12个方格中以满足相应的运算，问有多少种方法

为什么想到 dfs？

因为我们要对每个方格中的数字进行选择，相当于13个数字中选择12个数字进行排列，因而我们考虑dfs，将4x4阶矩阵拉成一维数组，让12个数进行全排列后填入方格中，在确定完一个方格后继续深搜下一个方格，直到全部方格都被填满时，相当于走到了dfs的死胡同，即为一种排列，我们判断此时是否满足条件即可

1. vis数组记录该数是否被使用过
2. num数组记录每个方格中的数

对于dfs：

由于为排列，我们选择从idnex=1开始深搜，依次有序地填入：

1. 结束条件：index==13（12个空格均被填满）且满足运算；
2. 遍历1~13，如果没有被标记过，则该数可选；
3. 标记与回溯：这里要标记与回溯两个值，一个是当前点的访问状态，另一个是num中该位置上的数字
4. 剪枝：在dfs中剪枝十分重要，可以极大地降低时间复杂度，我们在后续也会详细讨论

这道题要注意剪枝，因为每填入三个方格时，都可以进行一个完整的运算，如果当前运算都不满足了，则后面的运算就算满足也没有用，于是可以舍弃这种情况了（回溯）

代码实现：

def dfs(index):
    global res
    if index==4 and num[1]+num[2]!=num[3]:
        return
    if index==7 and num[4]-num[5]!=num[6]:
        return
    if index==10 and num[7]*num[8]!=num[9]:
        return
    if index==13 and num[10]/num[11]==num[12]:
        res+=1

    for i in range(1,14):
        if not vis[i]: # 表示该数字未被用过
            vis[i]=1
            num[index]=i # 添加index位置上的数为i
            dfs(index+1) # 找下一个位置
            num[index]=0 # 回溯
            vis[i]=0

res=0
vis=[0]*14 # 标记数字是否被用过
num=[0]*14 # 存方格内数字
dfs(1)
print(res)

③全球变暖

全球变暖

思路分析：

对dfs:

本题要求会被完全淹没的岛屿，我们不难想到对图进行深搜判断满足条件的岛屿，所以这道题的难点其实是如何进行dfs？

我们先思考，某一块陆地什么时候会被全部淹没，即该陆地的四周没有陆地的时候，也就是存在直接接触海洋的部分，所以，我们的思路就是，对每一块陆地进行判断其是否会被淹没；

那和dfs有什么关系呢？

因为这里是要判断一整个岛屿是否会被淹没而不是一块陆地，所以，当我们访问到一块陆地时，我们还要根据连通性对该岛屿上的其他陆地进行dfs深搜判断，要遍历完所有陆地的情况才能得出岛屿的情况：

这时岛屿内没有一块陆地四周是四周都有陆地的，所以会被淹没

💡 其实，只要岛屿上有一块陆地不会被淹没就说明岛屿不会被淹没了

1. graph用于存图：这里要注意，要对graph进行升维，因为深搜的时候可能存在这种情况：
   

   此时，左上角的陆地其实是不会被淹没的（因为没有与海洋直接接触），但我们发现graph会超出边界，无法判断，所以，我们默认四周都是陆地所组成的墙，将图包裹在其中

   图优化：

2. vis用于标记访问过的陆地，防止多解出现：

   因为当我们遇到一块陆地并进行深搜时，我们其实根据连通性已经访问过了岛屿上所有的陆地，因此，我们再遇到访问过的陆地时，应该直接跳过（因为它代表的是访问过的岛屿，不能再判断一遍）

代码实现：

import sys
sys.setrecursionlimit(60000)   # 设置递归深度

num=0
def dfs(x,y):
    global num,flag,vis
    vis[x][y]=1 # 每访问到一个陆地 就标记该陆地
    if graph[x-1][y]=='#' and graph[x+1][y]=='#' \\
        and graph[x][y+1]=='#' and graph[x][y-1]=='#':
        flag=1 # 表示该岛屿上存在陆地不会被淹没，即表示该岛屿不会被淹没

    for i,j in [(1,0),(-1,0),(0,1),(0,-1)]:
        nx=x+i; ny=y+j # 继续dfs连通的陆地
        if vis[nx][ny]==0 and graph[nx][ny]=='#':
            dfs(nx,ny)

n=int(input())
vis=[[0]*(n+2) for _ in range(n+2)]
 # 存图
graph=[]
for _ in range(n):
    graph.append(['#']+list(input())+['#'])
graph.insert(0,['#' for i in range(n+2)])
graph.append(['#' for i in range(n+2)])

for i in range(1,n+1):
    for j in range(1,n+1):
        if vis[i][j]==0 and graph[i][j]=='#': # 遍历整个图 当遇到陆地时dfs
            flag=0
            dfs(i,j)
            if flag==0: # 题目求的是被淹没的岛屿数...
                num+=1
print(num)

三.dfs的剪枝优化

1.剪枝技巧

①剪枝：

💡 剪枝：顾名思义，就是通过一些判断，砍掉搜索树上不必要的子树，往往有时在当前状态已经不满足条件了，那么我们其实没必要对这个分支进行搜索，砍掉这个子树，就是剪枝

这是dfs中的一个常见操作，由于dfs本质上是一种十分暴力的，其按照一个固定的搜索方式对所有的情况进行枚举，并从中找到我们所求的解，因此，我们需要通过剪枝对dfs进行优化，从而降低时间复杂度

②剪枝的使用场景：

我们往往考虑剪枝的关键是：怎么剪？在哪里剪？

我们在之前的题目中遇到了剪枝，现在来系统地了解其使用场景

对于dfs的剪枝，有以下几种方式：

2.剪枝的应用

①剪格子

剪格子

思路分析：

题目中给了一个nxm阶的矩阵，我们要求得的方格区域为：

💡 ①包含左上角的格子；②区域连续；③区域内和为矩阵总和的一半

1. vis用于标记所走过的格子
2. flag用于判断解是否存在
3. g用于存图

对于dfs：

1. 结束条件：①flag=True，表示有解，否则为0；②和为一半

2. 剪枝优化：

🧐 ①如果当前的方格内和大于总和的一半了（已经不满足条件了，不用继续dfs）；
②当前的方格数大于满足条件的其他情况的方格数（说明不是最优解）

3. 遍历四个方向，若没有越界且该点未被访问过，则继续dfs

4. 传入参数：

💡 ①方格坐标（x，y）；②当前所含方格的总和 k； ③当前的格子数 c

代码实现：

res=float('inf')
flag=False
def dfs(x,y,k,c):
    global res,flag
    if 2*k>s and c>res:
        return
    if 2*k==s:
        flag=True
        res=c
    for i,j in [(1,0),(-1,0),(0,1),(0,-1)]:
        nx=x+i; ny=y+j
        if 0<=nx<=n-1 and 0<=ny<=m-1 and vis[nx][ny]==0:
            vis[nx][ny]=1
            dfs(nx,ny,k+g[nx][ny],c+1)
            vis[nx][ny]=0

m,n=map(int,input().split())
vis=[[0]*m for _ in range(n)]
g=[]
s=0
for i in range(n):
    l=list(map(int,input().split()))
    g.append(l)
    s+=sum(l)

vis[0][0]=1 # 传入左上角的格子
dfs(0,0,g[0][0],1)

if flag:
    print(res)
else:
  print(0)

②路径之谜

路径之谜

思路分析：

💡 dfs：本题为路径问题，要求输出一条路径，用dfs很合适，因为深搜过程中，会自然生成一条路径

理解题意：每到一个格子，就要将其行和列上对应的靶数+1，由此，我们可以换一个思路，我们已知各行各列上的靶子数，每到一个方格时，我们就使其对应的行列上的数 -1，走到终点时，各行各列的数字应该全为0：

1. a,b数组分别用于存放各列和各行的靶数
2. vis用于标记走过的点
3. graph用于存图
4. path数组用于保存路径

对于dfs:

1. 结束条件：①到达终点坐标；②各行各列上对应的数字全部清为0

2. 遍历四个方向，若没有越界且该点未被访问过，就继续深搜

3. 剪枝优化：

🧐 若当前所在坐标对应的行列上的数字已经被减到小于0，说明当前已经不满足条件，不需要继续dfs

代码实现：

import sys
sys.setrecursionlimit(100000)
def dfs(x,y):
    global path
    if a[y]<0 or b[x]<0:
        return
    if x==n-1 and y==n-1:
        flag=1
        for i in range(n):
            if a[i]!=0 or b[i]!=0:
                flag=0
                return
        if flag==1:
            for j in range(len(path)):
                print(path[j],end=' ' if j!=len(path)-1 else '')

    for i,j in [(1,0),(-1,0),(0,1),(0,-1)]:
        nx=x+i; ny=y+j
        if 0<=nx<=n-1 and 0<=ny<=n-1 and vis[nx][ny]==0:
            vis[nx][ny]=1
            path.append(graph[nx][ny])
            a[ny]-=1; b[nx]-=1
            dfs(nx,ny)
            a[ny]+=1; b[nx]+=1
            path.pop()
            vis[nx][ny]=0

n=int(input())
a=[i for i in map(int,input().split())] # x轴上各列对应的数
b=[j for j in map(int,input().split())] # y轴上各行对应的数
graph=[] # 存图
for i in range(n):
    graph.append([k for k in range(4*i,4*(i+1))])
path=[]
vis=[[0]*n for i in range(n)]
vis[0][0]=1
a[0]-=1;b[0]-=1
path.append(graph[0][0])
dfs(0,0)

③四阶幻方

四阶幻方

思路分析：

理解题意：要找到行、列以及两个对角线的和都相等的所有矩阵，且固定左上角为1，即为对数字2~16进行全排列，再填入矩阵的相应位置，因此，我们想到用dfs

对于dfs：

因为第一个位置确定，我们从矩阵的第二个位置开始填入数字：

1. 结束条件：①位置数为16时，代表矩阵被填满；②行、列以及两个对角线的和都相等
2. 在当前层（层数即代表当前填入矩阵的位置数），对该位置上的元素进行遍历（用数字2~16依次填入），如果该数字未被使用过，则继续dfs
3. 剪枝优化：

（这道题的剪枝优化十分有意思，是剪枝很好的体现）

之前一直说填入矩阵相应的位置数，那你也没说位置在哪呀？

确定这个矩阵填入的位置数，其实就是确定填入矩阵的顺序，如果按照之前的逐行搜索，再对每一行的列进行遍历，有两层for循环，所以这里我们先优化为一维数组来表示一个矩阵，但按这样的方式填入，全排列2~16，时间复杂度还是很高

如图（为一般矩阵的填入顺序）：

由此，我们想到了dfs的常用技巧——剪枝

但是又来了，谁都知道要剪枝，那么剪枝应该怎么剪呢？

所以，这就和我们将数字填入矩阵的顺序就有很大关系了

如图（特定的填入矩阵的顺序）：

我们规定这样一个矩阵，其中图中矩阵内的数字为一维数组的下标（索引）

为什么要这样设计呢？这样设计有什么好处吗？

我们模拟一下，对于4x4的矩阵而言，每一行/列/对角线的和应为：（1+…+16）/ 4 = 34

1. 第一次（index==4）：当我们向矩阵内填入了四个数时（包括1），这时，我们最多已经可以确定一个表达式了（假设先是行）（最多是因为防止乱填），这时，我们可以判断第一行上的和是否等于34——1次剪枝；

   

2. 第二次（index==4）：第一次确定了行，这次我们确定列，因为这时候每一列上都有一个元素已经在第一次被填入了，所以这时我们只需要新填入3个数字即可再得到第一列得表达式，判断是否和为34——2次剪枝；

   

3. 第三次（index==4）：第二次确定了列，这次我们确定行，同样也需要新填入3个数字，可得到第二行得表达式，判断是否和为34——3次剪枝；

   

4. 第四次（index==4）：这一次有点特殊，我们发现这时候，对角线上得元素只剩下一个就填满了，所以，对这一个对角线可以得到一个表达式，判断是否和为34——4次剪枝；

😄 以此类推，每一次都找到填入最少的数就可以得到一个表达式的填入方式，尽可能多地进行剪枝，降低时间复杂度

代码实现：

import sys
sys.setrecursionlimit(1000000)
def dfs(x):
    global cnt
    # 剪枝
    if x>=4 and a[0]+a[1]+a[2]+a[3]!=34:  return   # 第一行
    if x>=7 and a[0]+a[4]+a[5]+a[6]!=34:  return    # 第一列
    if x>=10 and a[4]+a[7]+a[8]+a[9]!=34:  return   # 第二行
    if x>=11 and a[3]+a[8]+a[10]+a[6]!=34:  return  # 对角线
    if x>=12 and a[1]+a[7]+a[10]+a[11]!=34:  return # 第二列
    if x>=14 and a[5]+a[10]+a[12]+a[13]!=34:  return # 第三行
    if x>=15 and a[2]+a[8]+a[12]+a[14]!=34:  return  #第三列
    if x>=16 and (a[3]+a[9]+a[13]+a[15]!=34 or a[6]+a[11]+a[14]+a[15]!=34
        or a[0]+a[7]+a[12]+a[15]!=34): return # 最后一行、列、对角线
    if x==16:  cnt+=1

    # dfs递归
    for i in range(2, 17):  # 即每一个位置 用2~16去遍历 全排列
        if vis[i] == 0:
            a[x] = i
            vis[i] = 1
            dfs(x+1)
            vis[i] = 0

cnt=0
a=[0]*17
a[0]=1
vis=[0]*17
vis[0]=1
dfs(1)  # 从位置1开始搜索
print(cnt)
# 416

④分考场

分考场

思路分析：

理解题意：要求将所有考生分到最少的考场中，相当于有条件地进行组合，选择考场数最少的组合方式即为本题的解，于是我们想到可以使用dfs实现这样的组合，可以枚举所有组合以得到最优解

组合的思想是当前状态下选或不选，面对新加入的一个考生，我们要考虑的是，能选还是不能选，这需要根据条件而定：

🧐
核心思想——贪心：要达到最少的考场，我们每次应该尽可能地将新考生加入已开辟的考场中，如果所有已开辟的考场都不能满足加入该新考生的条件，我们再考虑开辟新的考场

准备：

1. 二维数组t 用于存放考生之间的关系，1为认识，0为不认识
2. 二维数组p 用于存放考场信息，[i]表示第i个考场，[i][j]表示第i个考场下位置为 j 上的人

对于dfs：

1. 结束条件：①当前人数大于总人数时，说明已经将所有人分配完成，记录此时的房间数

2. 剪枝：若考场数≥当前得到的最小考场数时，不用再继续进行dfs，因为不是最优解

   （这里要注意等号时也是不用再继续考虑的，没加等号会有一个案例超时，所以要让剪枝最大程度地优化）

3. 两次dfs思路：

   这道题需要进行两次dfs，为什么有两次dfs？这里当然不是说dfs嵌套dfs…

   有前面的分析得知，我们需要考虑加入的考生能选或不能选的情况，所以类似组合的思想：

   1. 当能加入已有考场时进行一次dfs（选 ）：

      遍历当前每一个考场，对每一个考场的每一个位置进行遍历，只有当该考场内的所有人与新加入的考生无关系时，才能加入，坐到最后一个位置上

   2. 当所有考场都加不进去时进行一次dfs（不选 ）：

      基遍历完所有的考场后，都不能加入，则开辟新的考场

✅ 若考场满足条件能选但最终不选，一定不是最优解

代码实现：

def dfs(a,room): #传入当前要加入的人和当前的房间数
    global res
    if room>=res: # 剪枝
        return
    if a>n: # 全部入座
        res=room
        return

    for i in range(1,room+1): # 我们先遍历当前所有的考场
        k=0
        while p[i][k]!=0 and t[p[i][k]][a]==0:
            k+=1 # 在当前考场，遍历考场内部，如果当前位置有人且于要加入的人无关，则去下一个位置
        if p[i][k]==0: # 找到空位了
            p[i][k]=a
            dfs(a+1,room)
            p[i][k]=0
    # 如果a无法加入任何一个考场
    p[room+1][0]=a
    dfs(a+1,room+1)
    p[room+1][0]=0

n=int(input())
t=[[0]*(n+1) for i in range(n+1)] # 关西网
p=[[0]*(n+1) for j in range(n+1)] # 考场情况:[i]表示第i个考场 [i][j]表示第i个考场下的j位置
for _ in range(int(input())):
    x,y=map(int,input().split())
    t[x][y]=t[y][x]=1 # 表示两人有关系
res=n # 初始化为n,怎么也不会超过n个考场吧
dfs(1,0)
print(res)

四.dfs的树上应用

1.树的遍历

①二叉树的层序遍历

二叉树的层序遍历

本题为层序遍历题，下节中的bfs可以更好地处理该问题，但dfs也可以做：

思路分析：

由于题目要求每一层的节点都是从左到右遍历，因此递归时也要先递归左子树、再递归右子树

dfs主要要解决的是：

dfs不是按照层次遍历的，为了让递归的过程中同一层的节点放到同一个列表中，在递归时要记录每个节点的深度 level，递归到新节点要把该节点放入 level 对应列表的末尾

💡 当遍历到一个新的深度 level，而最终结果 res 中还没有创建 level 对应的列表时，应该在 res 中新建一个列表用来保存该
level 的所有节点

对于dfs：

✅ 传入参数为（根节点root，层级数level，结果列表res）

1. 先判断根节点是否为空，否则直接返回

2. 如果当前层数等于结果列表长度len(res)==level

   表示上一层的层级数和结果列表长度相同，而到了当前新的一层，需要向后添加新的列表以存放该层结点

3. 依次判断左右结点，如果不为空，分别进行dfs

代码实现：

# Definition for a binary tree node.
class TreeNode(object):
    def __init__(self, x):
        self.val = x
        self.left = None
        self.right = None

class Solution(object):
    def levelOrder(self, root):
        """
        :type root: TreeNode
        :rtype: List[List[int]]
        """
        res = []
        self.level(root, 0, res) 
        return res

    def level(self, root, level, res):
        if not root:  # 如果为空，则结束
						return
        if len(res) == level:  
						res.append([])
        res[level].append(root.val)
        if root.left: 
						self.level(root.left, level + 1, res)
        if root.right: 
						self.level(root.right, level + 1, res)

五.总结

​   本章介绍了BFS广度优先遍历的相关知识，包括字典的创建、修改和遍历，以及双向广搜的概念、实现和应用。其中，双向广搜可以优化单向搜索的时间复杂度，适用于确定起点和终点的情况，以上如有错误欢迎指正~~，感谢！！！

觉得本篇有帮助的话,就赏个三连吧~