二叉树相关（leetcode)

最新推荐文章于 2025-05-16 21:02:30 发布

我所向披靡

最新推荐文章于 2025-05-16 21:02:30 发布

阅读量1.1k

点赞数 29

文章标签： leetcode 算法职场和发展

本文链接：https://blog.youkuaiyun.com/qq_72994250/article/details/135819859

版权

#二叉树的三种深度遍历：

LeetCode94、二叉树的中序遍历

class Solution:
    def dfs(self, ans, node):
        # 如果节点为空，返回
        if node is None:
            return
        # 递归遍历左子树
        self.dfs(ans, node.left)
        # 将当前节点的值加入结果列表
        ans.append(node.val)
        # 递归遍历右子树
        self.dfs(ans, node.right)

    def inorderTraversal(self, root):
        # 初始化答案列表为空列表
        ans = list()
        # 递归函数入口，传入根节点
        self.dfs(ans, root)
        # 返回结果列表，即为答案
        return ans

LeetCode144、二叉树的前序遍历

class Solution:
    def dfs(self, ans, node):
        # 如果节点为空，返回
        if node is None:
            return
        # 将当前节点的值加入结果列表
        ans.append(node.val)
        # 递归遍历左子树
        self.dfs(ans, node.left)
        # 递归遍历右子树
        self.dfs(ans, node.right)

    def preorderTraversal(self, root):
        # 初始化答案列表为空列表
        ans = list()
        # 递归函数入口，传入根节点
        self.dfs(ans, root)
        # 返回结果列表，即为答案
        return ans

LeetCode145、二叉树的后序遍历

class Solution:
    def dfs(self,ans,node):
        if node is None:
            return
        self.dfs(ans,node.left)
        self.dfs(ans,node.right)
        ans.append(node.val)
#对左做递归->对右做递归->访问根结点        
    def postorderTraversal(self,root):
#空答案列表        
        ans =list()
        self.dfs(ans,root)
        return ans

#从深度遍历序列还原二叉树

我们知道：

前序：根左右

中序：左根右

后序：左右根

要想确定二叉树有两种方式：

给出序列：

（1）先序+中序

（2）后序+中序

LeetCode105. 从前序与中序遍历序列构造二叉树

给出了（1）先序+中序：preorder = [3,9,20,15,7], inorder = [9,3,15,20,7]

我们需要将二叉树还原出来：

第一步：

先找根

根据先序 : [3,9,20,15,7]我们可以先确定3为第一层的根结点。

再看中序：[9,3,15,20,7]，3的位置，可知[9]在3的左子树，而[15，20，7]在3的右子树。

接下来确定右部的第二层根结点，在前序中[3,9,20,15,7],根左右，得出根结点为20

再看中序[9,3,15,20,7]，20的位置，可知15在20的左子树，而7在20的右子树。

完成还原：

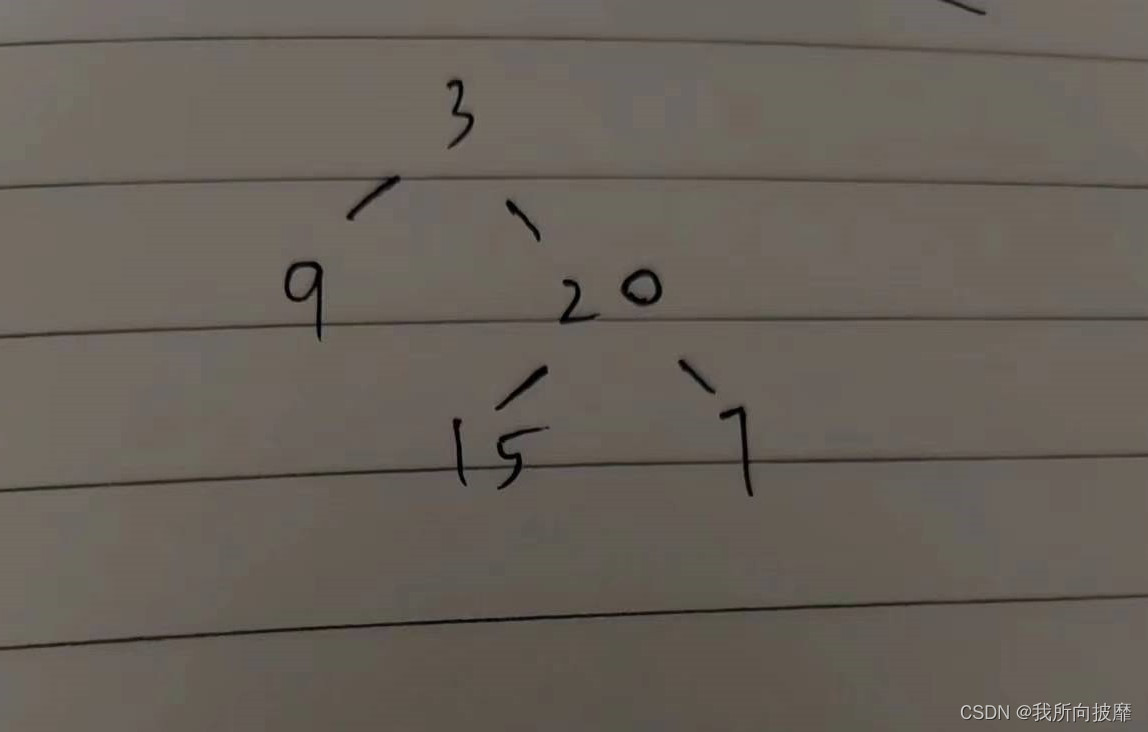还原一二叉树，不论序列有多长，这其实是一个不断递归的过程：找子树根节点，找左右子树.....

再看一个例子：

给出:先序[3,9,10,20,15,5,7] 中序：[10，9，3，15，5，20，7]

先找到3为第一层根节点，看中序把左子树和右子树分割开，

现在我们知道左子树的内容比较简单，再看右子树的序列，pre[20,15,5,7] in[15,5,20,7]

又能从先序找出右子树根结点20，从中序序列发现[15,5]为20的左子树，[7]为20的右子树，完成还原。

那么如何用代码逻辑实现这个过程？

还原二叉树的过程就是将两个序列数组不断拆分成子数组的过程，我们将用两个指针来代替这个过程：先给中序序列头，尾添加两个指针in.start,in.end，in.start,in.end表示我们将整个中序序列选中

在前序序列的头添加指针pre.start；由我们先前还原二叉树的步骤，先找到3（这个3是由前序中的指针pre.start先取得的），在中序序列中添加i指针：idx；在中序数组中[10,9,3,15,5,20,7]

分出左子树【10，9】，右子树【15，5，20，7】，要实现这个递归操作，其实就是用索引来完成这个过程：

# 对于任何一颗子树：

# 根节点一定在前序遍历数组的第一个位置（pre.start）

# 可以找到根节点在中序遍历数组中的位置（idx），其左边为左子树（in.start2,in.end2），右边为右子树（in.start3,in.end3）

# 然后对左子树（idx-1）和右子树（idx+1）进行递归操作

LeetCode 105、从前序与中序遍历序列构造二叉树:

# Definition for a binary tree node.
# class TreeNode:
#     def __init__(self, val=0, left=None, right=None):
#         self.val = val
#         self.left = left
#         self.right = right

# 对于任何一颗子树：
# 根节点一定在前序遍历数组的第一个位置
# 可以找到根节点在中序遍历数组中的位置，其左边为左子树，右边为右子树
# 然后对左子树和右子树进行递归操作
class Solution:
    def buildTree(self, preorder: List[int], inorder: List[int], ) -> Optional[TreeNode]:
        # 构建一个哈希表，key为节点的值，value为节点在中序遍历数组中的索引
        # 方便直接通过节点值取到下标
        dic = {val: i for i, val in enumerate(inorder)}
        n = len(inorder)
        # 递归入口
        return self.help(dic, preorder, inorder, 0, 0, n-1)

    def help(self, dic, preorder, inorder, pre_start, in_start, in_end):
        # 递归终止条件：若遍历区间不存在，返回空节点
        if in_start > in_end:
            return None

        # 获得当前区间的根节点的值node_val，为preorder[pre_start]
        node_val = preorder[pre_start]
        # 获得该节点在中序遍历数组中的位置
        idx_node = dic[node_val]

        # 构建节点node
        node = TreeNode(node_val)
        
        
        # 进行递归

        # pre_start
        # ↓
        # 3 | 9  5 | 20  15  7
        #     ↑       ↑             左子树和右子树的pre_start

        # in_start        in_end
        # ↓               ↓
        # 9  5 | 3 | 15  20  7
        #        ↑
        #        idx_node

        # 9  5 | 3 | 15  20  7
        # ↑  ↑                      左子树的in_start和in_end
        #             ↑      ↑      右子树的in_start和in_end
        
        node.left = self.help(dic, preorder, inorder, pre_start + 1, in_start, idx_node - 1)
        node.right = self.help(dic, preorder, inorder, pre_start + (idx_node - in_start) + 1, idx_node + 1, in_end)

        # 将该节点回传
        return node

哈希表知识候补：

LeetCode106、从中序与后序遍历序列构造二叉树

思路基本一致：

# Definition for a binary tree node.
# class TreeNode:
#     def __init__(self, val=0, left=None, right=None):
#         self.val = val
#         self.left = left
#         self.right = right

# 对于任何一颗子树：
# 根节点一定在后序遍历数组的最后一个位置
# 可以找到根节点在中序遍历数组中的位置，其左边为左子树，右边为右子树
# 然后对左子树和右子树进行递归操作
class Solution:
    def buildTree(self,  inorder: List[int],postorder: List[int], ) -> Optional[TreeNode]:
        # 构建一个哈希表，key为节点的值，value为节点在中序遍历数组中的索引
        # 方便直接通过节点值取到下标
        dic = {val: i for i, val in enumerate(inorder)}
        n = len(inorder)
        # 递归入口
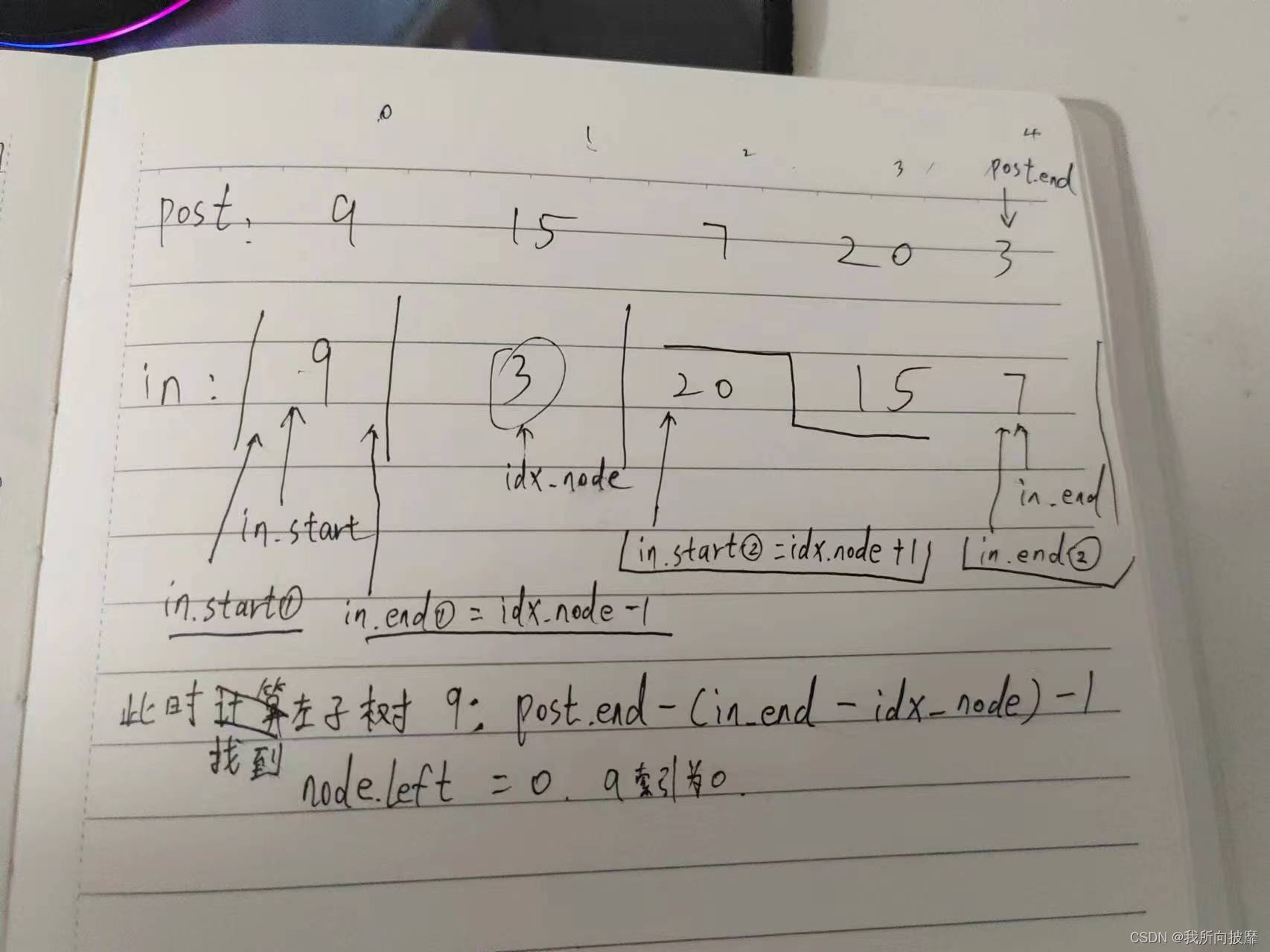
        return self.help(dic, postorder, inorder, n-1, 0, n-1)

    def help(self, dic, postorder, inorder, post_end, in_start, in_end):
        # 递归终止条件：若遍历区间不存在，返回空节点
        if in_start > in_end:
            return None

        node_val =postorder[post_end]
        # 获得该节点在中序遍历数组中的位置
        idx_node = dic[node_val]

        # 构建节点node
        node = TreeNode(node_val)
        
    
        node.left = self.help(dic, postorder, inorder, post_end-(in_end-idx_node)-1, in_start, idx_node - 1)
        node.right = self.help(dic, postorder, inorder, post_end -1, idx_node + 1, in_end)
        # 将该节点回传
        return node

二叉搜索树的定义、查找、增加与删除：

二叉搜索树的效率就在于只需检索二个子树之一

与二分查找时间复杂度相同: O(log(n))

一种特殊的数据结构，能够高效查找；

LeetCode700、二叉搜索树中的搜索 LeetCoe701、二叉搜索树中的插入操作

BST二叉搜索树没有重复的节点,一次插入必有一次失败的查找

# Definition for a binary tree node.
# class TreeNode:
#     def __init__(self, val=0, left=None, right=None):
#         self.val = val
#         self.left = left
#         self.right = right
class Solution:
    def dfs(self, node, val):
        if val < node.val:
            if node.left is None:
                node.left = TreeNode(val)
                return
            self.dfs(node.left, val)
        elif val > node.val:
            if node.right is None:
                node.right = TreeNode(val)
                return
            self.dfs(node.right, val)
        else:
            if node.right is None:
                node.right = TreeNode(val)
                return
            self.dfs(node.right, val)
            
    def insertIntoBST(self, root, val):
        if root is None:
            return TreeNode(val)
        self.dfs(root, val)
        return root