递归函数的优化策略

递归函数的思想确实是编程中重要的一环，能帮助我们解决许多复杂的问题。

但是如何避免递归深度过大导致的性能问题，这是一个相对深入的话题。

就比如斐波那契数列，我们在写这个函数的时候就会面临一个问题

int fac2(int n)
{
	if (n > 2)
	{
		return fac2(n - 1) + fac2(n - 2);
	}
	else
		return 1;
}
int main()
{
	int ret = 0;
	int n = 0;
	scanf("%d", &n);	
	ret = fac2(n);
	printf("%d的斐波那契=%d", n, ret);
	return 0;
}

这是初学者练习递归函数最常用的一个范例，但是当我们输入一个特别大的数时就会面临一个问题，运行时间过长。时间复杂度过高，我们可以打印n==3的次数。

int count = 0;
int fac2(int n)
{
	
	if (n == 3)
	{
		count++;
	}
	
	if (n <= 2)
	{
		return 1;
		
	}
	else
		return fac2(n - 1) + fac2(n - 2);
}
int main()
{
	int ret = 0;
	int n = 0;
	scanf("%d", &n);	
	ret = fac2(n);
	printf("%d的斐波那契=%d\n", n, ret);
	printf("count=%d\n", count);
	return 0;
}

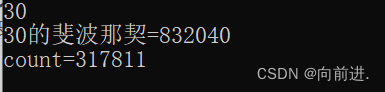
我们可以看出当n=30时，count 317811次，除此之外还有4，5，6，7等等。

我们要想一个办法减少他的时间复杂度，优化程序！！！

int fac3(int n)
{
	int a = 1;
	int b = 1;
	int c = 1;
	for (;n>2; n--)
	{
		c = a + b;
		a=b;
		b=c;
	}
	return c;
}
int main()
{
	int ret = 0;
	int n = 0;
	scanf("%d", &n);	
	ret = fac3(n);
	printf("%d的斐波那契=%d\n", n, ret);
	return 0;
}

使用递归+迭代，这样时间复杂度就会大大降低，为我们写程序时提供了一个很好的思路。

希望对大家有所帮助！！！