第二周学习笔记

代码实践：基于动态规划的强化学习

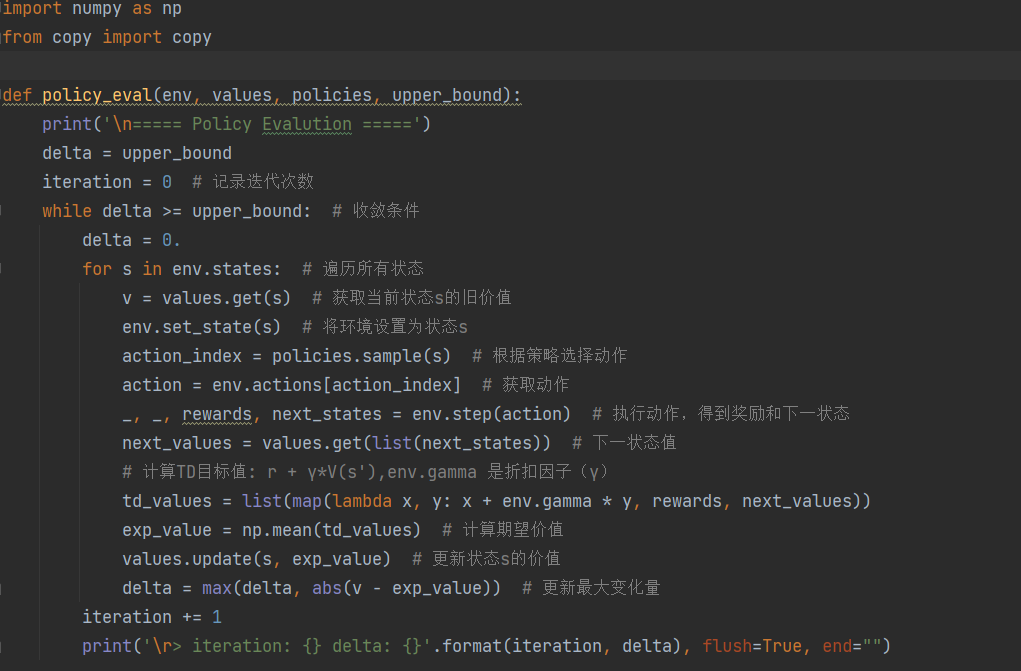
策略评估实施 ( Policy Evaluation Implementation)

输入：环境env，值函数表values，策略policies，收敛阈值upper_bound
功能：评估当前策略下的状态价值函数（贝尔曼期望方程迭代）

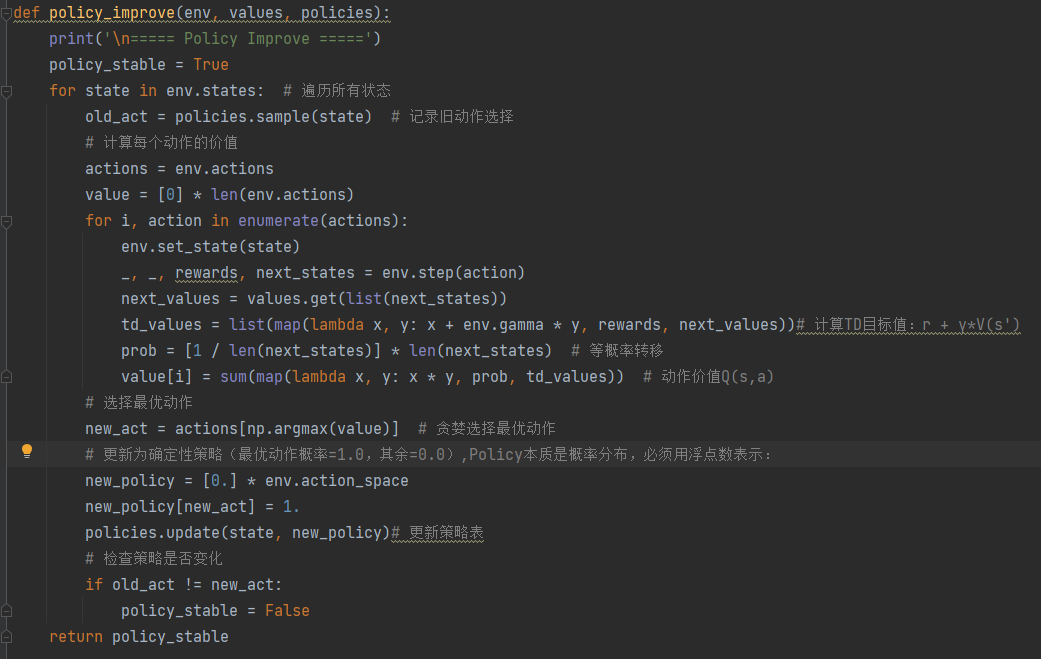
策略改进实现 (Policy Improvement Implementation)

输入：环境 env，值函数表 values，策略 policies
功能：根据当前价值函数生成更优的贪婪策略

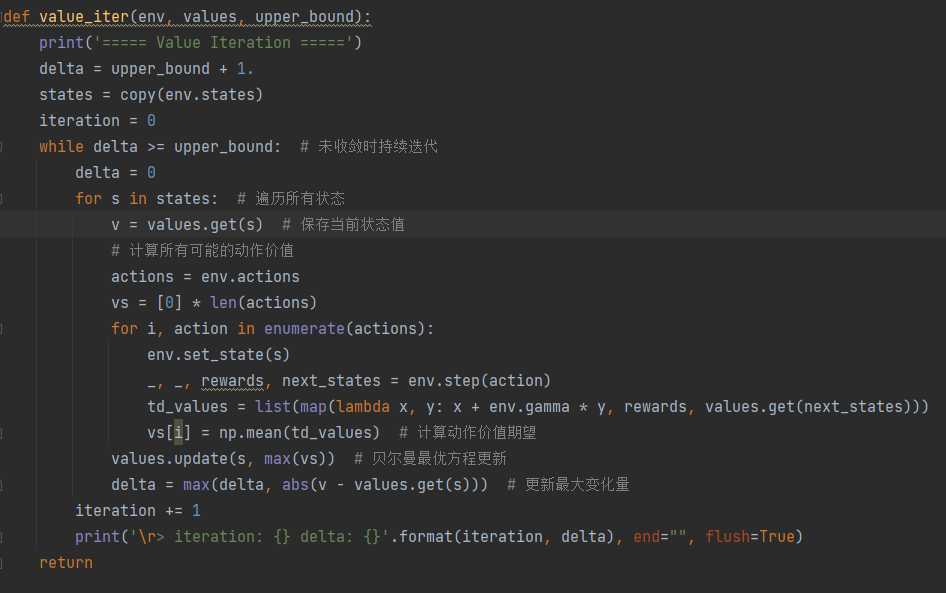
价值迭代实现 (Value Iteration Implementation)

输入：环境 env，值函数表 values，收敛阈值 upper_bound
功能：直接通过贝尔曼最优方程迭代求解最优价值函数

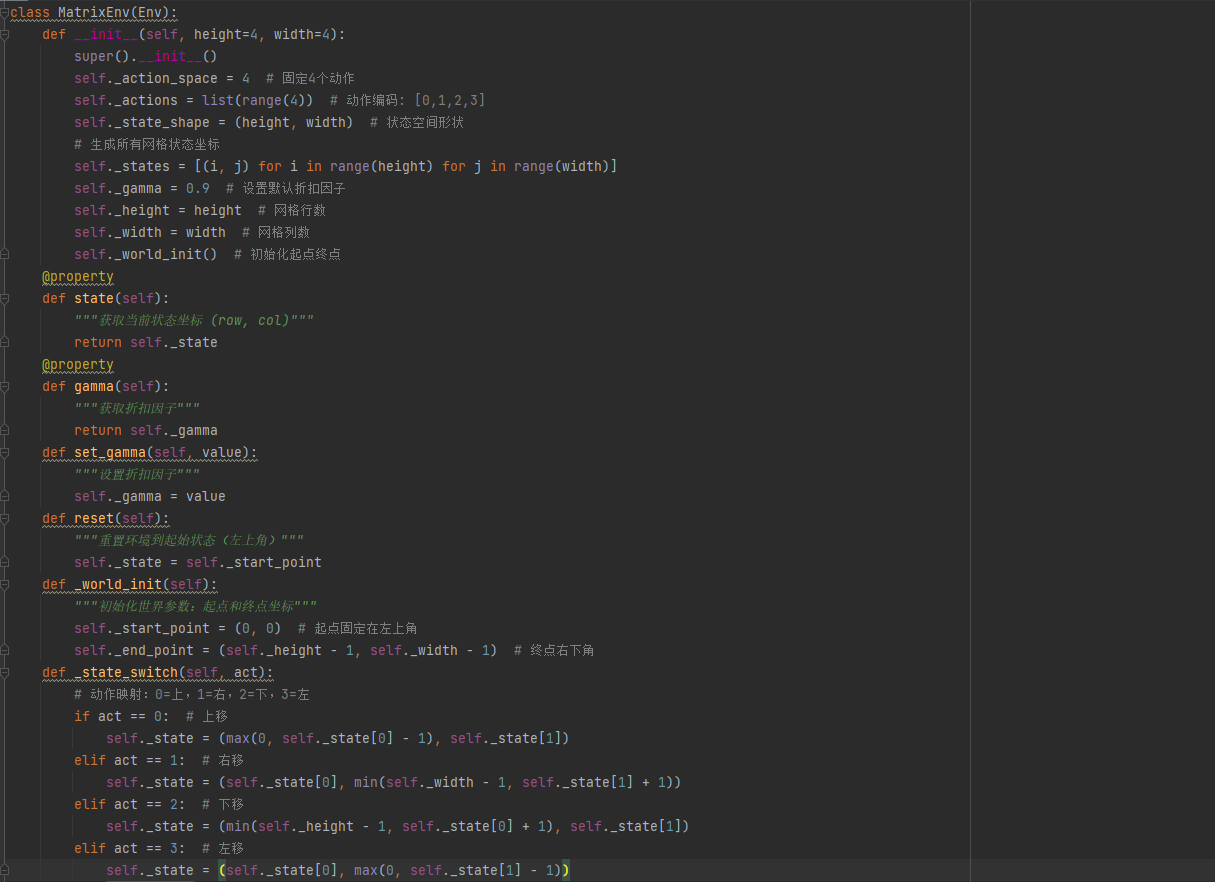
网格环境实现 (GridWorld Environment Implementation)

环境抽象基类，定义环境交互标准接口

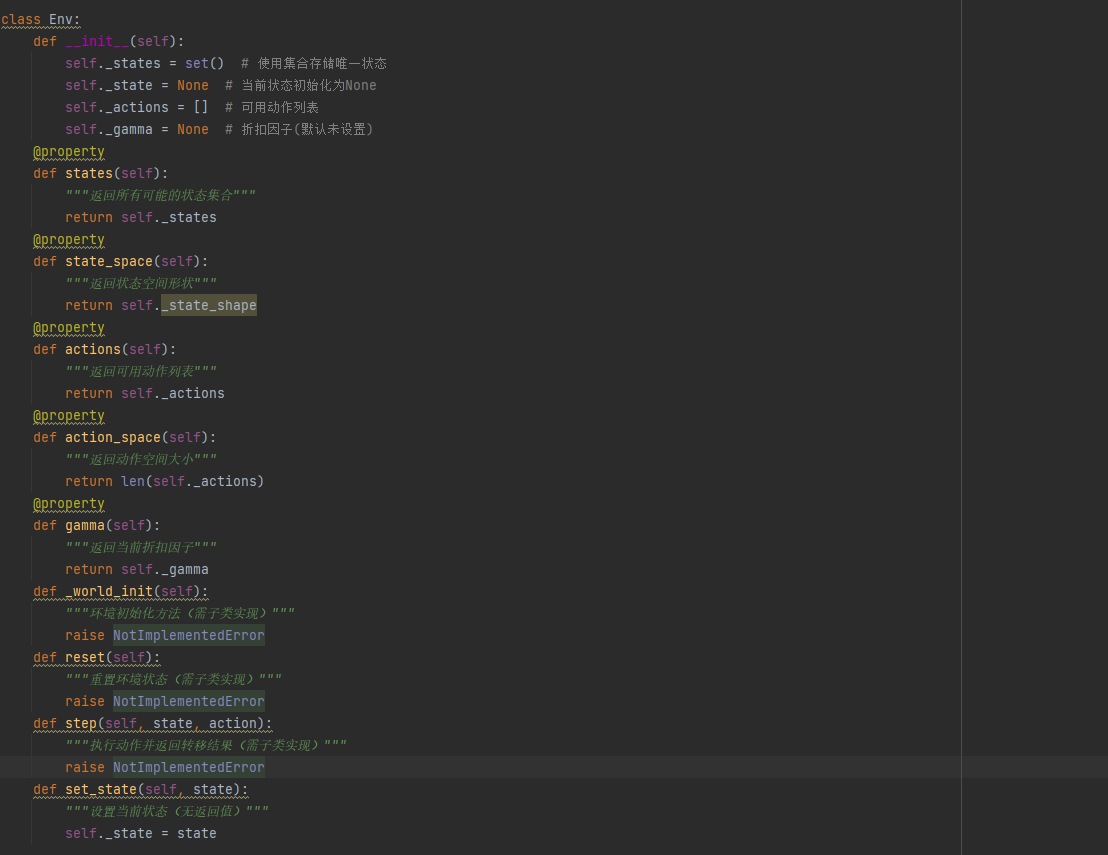
状态空间：二维网格坐标(row, col) 
动作空间：[0:上, 1:右, 2:下, 3:左]
奖励函数：终点奖励+1，其他为0

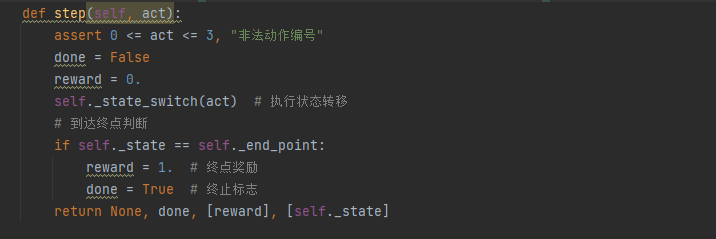
值函数表 (ValueTable)

功能：存储和更新状态价值函数 V(s)

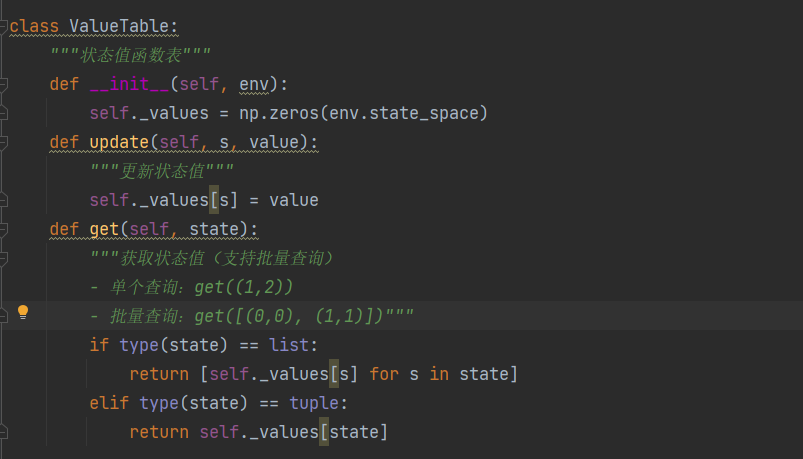
策略表(Policies)

功能：存储策略 π(a|s) 的概率分布

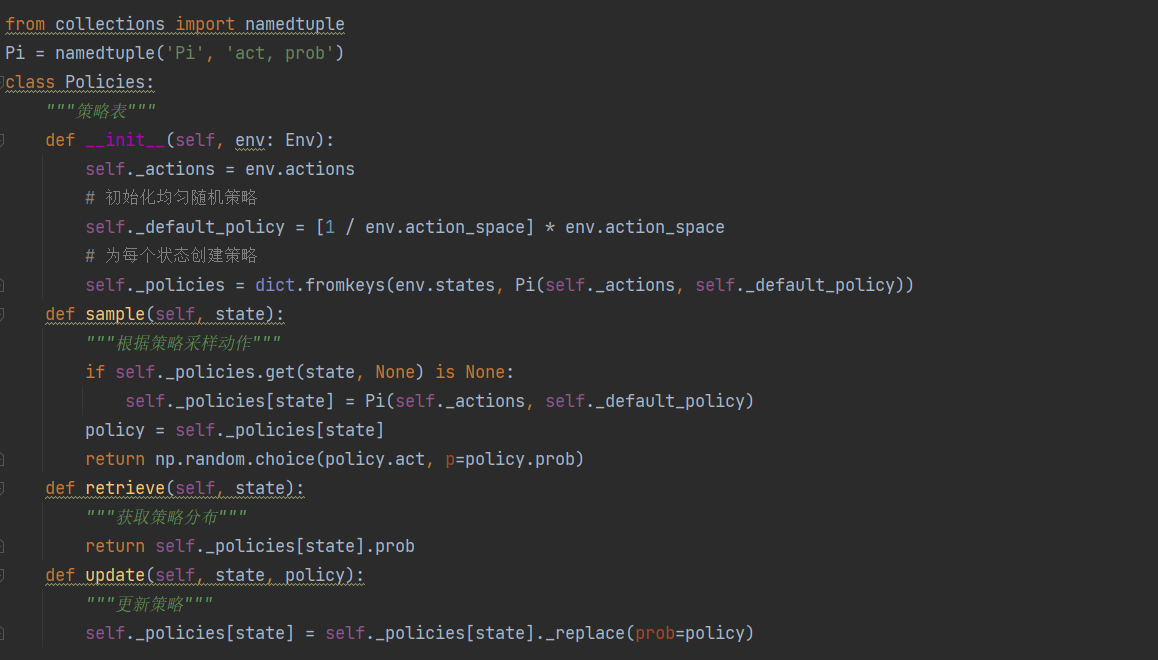
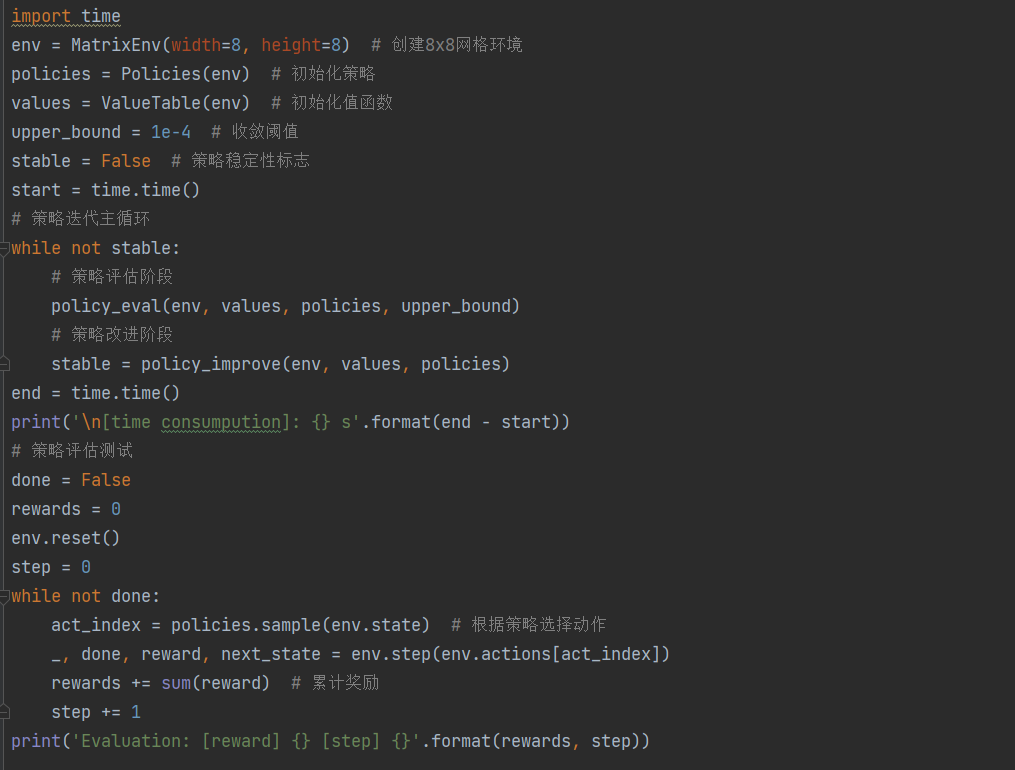
通过策略迭代求解矩阵游戏（Solving Matrix Game via Policy Iteration Learning）

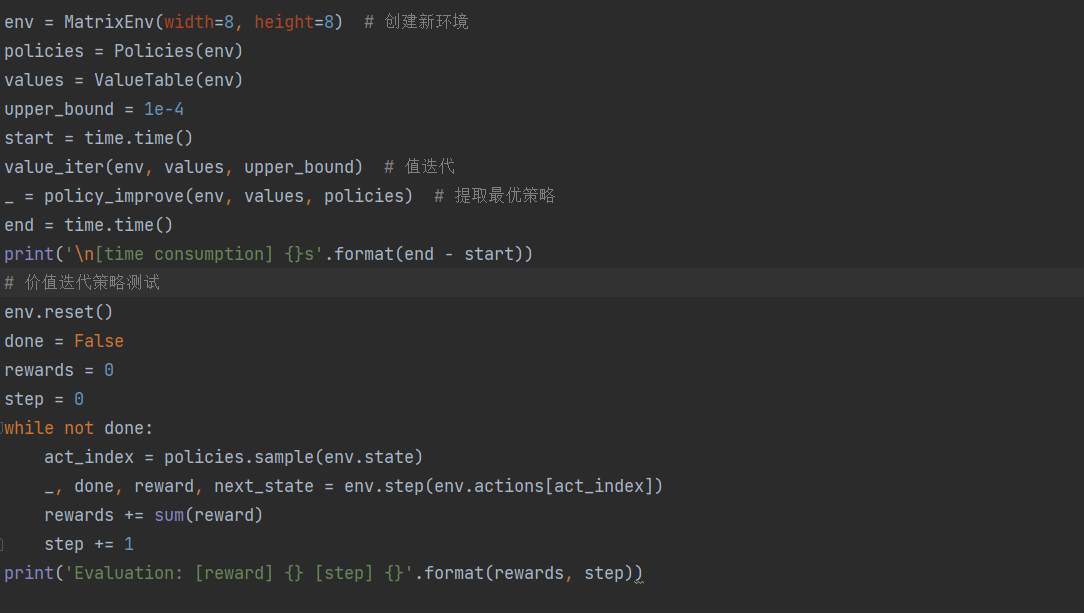
通过价值迭代求解矩阵游戏（Solving Matrix Game via Value Iteration Learning）

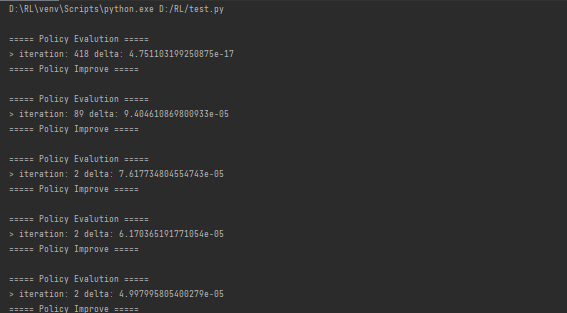
执行结果：

第一阶段（初始随机策略评估）

• 418次迭代：因为初始策略是随机的，需要更多迭代才能收敛

• 极小delta值：表示价值函数已充分收敛

后续阶段（策略优化过程）

• 迭代次数减少：随着策略改进，每次评估需要的迭代次数急剧下降

• delta逐步减小：显示策略正在快速优化

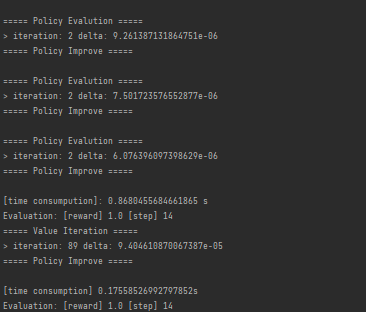
最终结果

• 策略迭代耗时0.868秒

• 价值迭代耗时0.175秒

• 两者都找到了最优路径（14步）

1 时序差分算法

1.1时序差分方法

        前面所学的马尔可夫决策过程是已知的，即要求与智能体交互的环境是完全已知的（例如迷宫或者给定规则的网格世界）。在此条件下，智能体其实并不需要和环境真正交互来采样数据，直接用动态规划算法就可以解出最优价值或策略。对于大部分强化学习现实场景（例如电子游戏或者一些复杂物理环境），其马尔可夫决策过程的状态转移概率是无法写出来的，也就无法直接进行动态规划。在这种情况下，智能体只能和环境进行交互，通过采样到的数据来学习，这类学习方法统称为无模型的强化学习（model-free reinforcement learning）。本章将要讲解无模型的强化学习中的两大经典算法：Sarsa 和 Q-learning，它们都是基于时序差分（temporal difference，TD）的强化学习算法。

        时序差分是一种用来估计一个策略的价值函数的方法，它结合了蒙特卡洛和动态规划算法的思想。时序差分方法和蒙特卡洛的相似之处在于可以从样本数据中学习，不需要事先知道环境；和动态规划的相似之处在于根据贝尔曼方程的思想，利用后续状态的价值估计来更新当前状态的价值估计。

        蒙特卡洛方法对价值函数的增量更新方式：

        蒙特卡洛方法必须要等整个序列结束之后才能计算得到这一次的回报G，而时序差分方法只需要当前步结束即可进行计算。具体来说，时序差分算法用当前获得的奖励加上下一个状态的价值估计来作为在当前状态会获得的回报，即： 

1.2 Sarsa算法

        可以直接用时序差分算法来估计动作价值函数Q：

 （为学习率，控制更新的步幅）

a′: 在新状态s’下选择的下一个动作。

        Q(s’, a’) 不会考虑所有可能的动作 a’，而是基于代理在状态 s’ 下实际采取的动作 a’。

        具体来说，SARSA算法在每一步中，会基于当前策略选择下一个动作 a’，然后根据这个实际采取的动作 a’ 来计算 Q(s’, a’)。这意味着它会考虑代理在当前策略下选择的动作 a’，并使用它来更新 Q 值。

        因此，SARSA在更新 Q 值时，考虑了代理的策略。这使得SARSA成为一个在策略上稳定的算法，因为它在学习时受到当前策略的限制。这也是SARSA和Q-learning之间的一个主要不同之处，因为Q-learning是离策略的，它选择的动作 a’ 不受当前策略的限制。

算法流程 ：

1. 初始化：

   • 对于所有状态 s ∈ S 和所有动作 a ∈ A(s)，初始化 Q(s, a) 为任意值（通常为 0）。

   • 选择初始状态 s。

   • 根据当前 Q 值（或其衍生策略，如 ε-greedy）选择初始动作 a。

2. 循环 (对每个 Episode 中的每一步)：

   • 在当前状态根据策略（如 -贪婪策略）选择动作 。

   • 观察环境返回的即时奖励 r 和下一个状态 s'。

   • 根据当前策略 π (由 Q 值定义，如 ε-greedy) 在状态 s' 选择下一个动作 a'。 (a' 的选择依赖于当前 Q 表，这是 on-policy 的关键体现)

   • 更新 Q 值： Q(s, a) ← Q(s, a) + α * (r + γ * Q(s', a') - Q(s, a))

     • α (Alpha) 是学习率 (Step Size)，0 < α ≤ 1。控制新信息覆盖旧信息的程度。

     • γ (Gamma) 是折扣因子，0 ≤ γ ≤ 1。

   • 更新状态和动作： s ← s', a ← a' (准备执行下一步)

3. 策略改进：
            随着值的更新，逐渐改善选择动作的策略。

Sarsa算法代码实践 

        智能体的起点是左下角的状态，目标是右下角的状态，智能体在每一个状态都可以采取 4 种动作：上、下、左、右。如果智能体采取动作后触碰到边界墙壁则状态不发生改变，否则就会相应到达下一个状态。环境中有一段悬崖，智能体掉入悬崖或到达目标状态都会结束动作并回到起点，也就是说掉入悬崖或者达到目标状态是终止状态。智能体每走一步的奖励是 −1，掉入悬崖的奖励是 −100，到达终止状态奖励为 0。

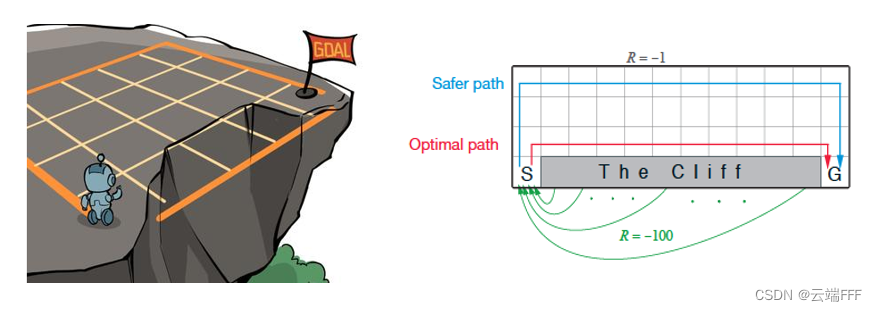 在悬崖漫步环境下尝试 Sarsa 算法，先配置环境（在计算就图像里，左上角通常是原点 (0,0)）

class CliffWalkingEnv:
    def __init__(self, ncol, nrow):
        self.nrow = nrow #网格的行数
        self.ncol = ncol #网格的列数
        self.x = 0  # 记录当前智能体位置的横坐标
        self.y = self.nrow - 1  # 记录当前智能体位置的纵坐标

    def step(self, action):  # 外部调用这个函数来改变当前位置
        # 4种动作, change[0]:上, change[1]:下, change[2]:左, change[3]:右。坐标系原点(0,0)
        # 定义在左上角
        change = [[0, -1], [0, 1], [-1, 0], [1, 0]]
        self.x = min(self.ncol - 1, max(0, self.x + change[action][0])) 
        # change变量 → 0x2000: [指针A, 指针B, 指针C, 指针D]，change[a][b]代表的是先找到第a个指针，然后再对应这个指针里面的第b个元素
        self.y = min(self.nrow - 1, max(0, self.y + change[action][1]))
        next_state = self.y * self.ncol + self.x
        reward = -1
        done = False #用来判断一个回合（Episode）是否应该结束
        if self.y == self.nrow - 1 and self.x > 0:  # 下一个位置在悬崖或者目标
            done = True
            if self.x != self.ncol - 1:
                reward = -100
        return next_state, reward, done

    def reset(self):  # 回归初始状态,坐标轴原点在左上角
        self.x = 0
        self.y = self.nrow - 1
        return self.y * self.ncol + self.x

维护一个表格Q_table()，用来储存当前策略下所有状态动作对的价值，在用 Sarsa 算法和环境交互时，用-贪婪策略进行采样，在更新 Sarsa 算法时，使用时序差分的公式。我们默认终止状态时所有动作的价值都是 0，这些价值在初始化为 0 后就不会进行更新。

class Sarsa:
    def __init__(self, ncol, nrow, epsilon, alpha, gamma, n_action=4):
        self.Q_table = np.zeros([nrow * ncol, n_action])  # 初始化Q(s,a)表格
        self.n_action = n_action  # 动作个数
        self.alpha = alpha  # 学习率
        self.gamma = gamma  # 折扣因子
        self.epsilon = epsilon  # epsilon-贪婪策略中的参数

    def take_action(self, state):  # 选取下一步的操作,具体实现为epsilon-贪婪
        if np.random.random() < self.epsilon: #生成一个0到1的随机数，检查是否小于epsilon值
            action = np.random.randint(self.n_action) #生成一个0到n_action-1的随机整数，随机选动作
        else:
            action = np.argmax(self.Q_table[state]) #查找数组中的最大值索引，返回数组中最大值对应的位置，选当前已知最好的动作
        return action

    def best_action(self, state):  # 用于打印策略
        Q_max = np.max(self.Q_table[state])  # 获取当前状态下所有动作中的最大Q值
        a = [0 for _ in range(self.n_action)]
        for i in range(self.n_action):  # 若两个动作的价值一样,都会记录下来
            if self.Q_table[state, i] == Q_max:
                a[i] = 1
        return a

    def update(self, s0, a0, r, s1, a1):
        td_error = r + self.gamma * self.Q_table[s1, a1] - self.Q_table[s0, a0]
        self.Q_table[s0, a0] += self.alpha * td_error

在悬崖漫步环境中运行 Sarsa 算法

ncol = 12
nrow = 4
env = CliffWalkingEnv(ncol, nrow)
np.random.seed(0)
epsilon = 0.1
alpha = 0.1
gamma = 0.9
agent = Sarsa(ncol, nrow, epsilon, alpha, gamma)
num_episodes = 500  # 智能体在环境中运行的序列的数量

return_list = []  # 记录每一条序列的回报
for i in range(10):  # 显示10个进度条
    # tqdm的进度条功能
    with tqdm(total=int(num_episodes / 10), desc='Iteration %d' % i) as pbar:
        for i_episode in range(int(num_episodes / 10)):  # 每个进度条的序列数
            episode_return = 0
            state = env.reset()
            action = agent.take_action(state)
            done = False
            while not done:
                next_state, reward, done = env.step(action)
                next_action = agent.take_action(next_state)
                episode_return += reward  # 这里回报的计算不进行折扣因子衰减
                agent.update(state, action, reward, next_state, next_action)
                state = next_state
                action = next_action
            return_list.append(episode_return)
            if (i_episode + 1) % 10 == 0:  # 每10条序列打印一下这10条序列的平均回报
                pbar.set_postfix({
                    'episode':
                    '%d' % (num_episodes / 10 * i + i_episode + 1),
                    'return':
                    '%.3f' % np.mean(return_list[-10:])
                })
            pbar.update(1)

episodes_list = list(range(len(return_list)))
plt.plot(episodes_list, return_list)
plt.xlabel('Episodes')
plt.ylabel('Returns')
plt.title('Sarsa on {}'.format('Cliff Walking'))
plt.show()

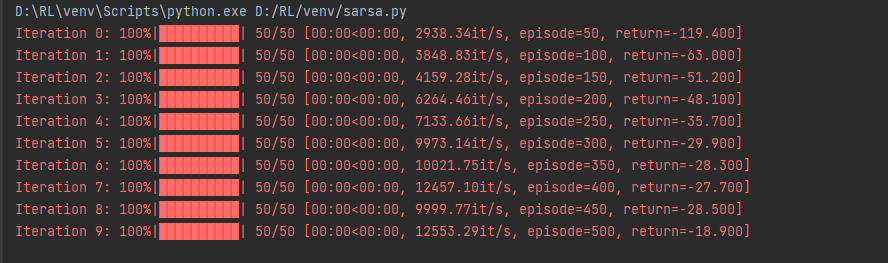
运行结果：

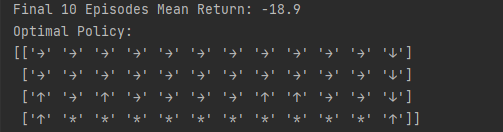
随着训练的进行，Sarsa 算法获得的回报越来越高。在进行 500 条序列的学习后，可以获得 −18.900的回报，此时已经非常接近最优策略。

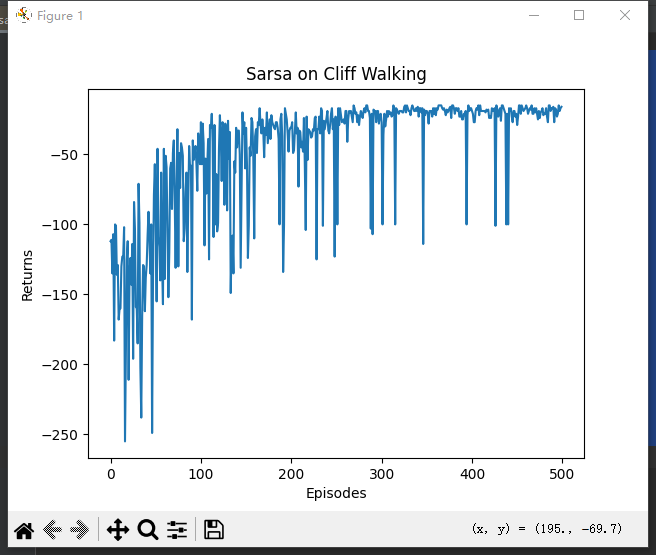
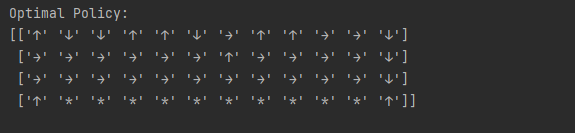
看一下 Sarsa 算法得到的策略在各个状态下会使智能体采取什么样的动作。可以发现 Sarsa 算法会采取比较远离悬崖的策略来抵达目标。

 

1.3多步Sarsa算法

        时序差分算法具有非常小的方差，因为只关注了一步状态转移，用到了一步的奖励，但是它是有偏的，因为用到了下一个状态的价值估计而不是其真实的价值。那有没有什么方法可以结合二者的优势呢？答案是多步时序差分！多步时序差分的意思是使用n步的奖励，然后使用之后状态的价值估计。用公式表示 ：

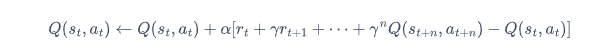
 多步Sarsa算法代码实践：

        在环境保持不变的情况下，在 Sarsa 代码的基础上进行修改，引入多步时序差分计算。

class nstep_Sarsa:
    """ n步Sarsa算法 """
    def __init__(self, n, ncol, nrow, epsilon, alpha, gamma, n_action=4):
        self.Q_table = np.zeros([nrow * ncol, n_action])
        self.n_action = n_action
        self.alpha = alpha
        self.gamma = gamma
        self.epsilon = epsilon
        self.n = n  # 采用n步Sarsa算法
        self.state_list = []  # 保存之前的状态
        self.action_list = []  # 保存之前的动作
        self.reward_list = []  # 保存之前的奖励

    def take_action(self, state):
        if np.random.random() < self.epsilon:
            action = np.random.randint(self.n_action)
        else:
            action = np.argmax(self.Q_table[state])
        return action

    def best_action(self, state):  # 用于打印策略
        Q_max = np.max(self.Q_table[state])
        a = [0 for _ in range(self.n_action)]
        for i in range(self.n_action):
            if self.Q_table[state, i] == Q_max:
                a[i] = 1
        return a

    def update(self, s0, a0, r, s1, a1, done):
        self.state_list.append(s0)
        self.action_list.append(a0)
        self.reward_list.append(r)
        if len(self.state_list) == self.n:  # 若保存的数据可以进行n步更新
            G = self.Q_table[s1, a1]  # 得到Q(s_{t+n}, a_{t+n})
            for i in reversed(range(self.n)):
                G = self.gamma * G + self.reward_list[i]  # 不断向前计算每一步的回报
                # 如果到达终止状态,最后几步虽然长度不够n步,也将其进行更新
                if done and i > 0:
                    s = self.state_list[i]
                    a = self.action_list[i]
                    self.Q_table[s, a] += self.alpha * (G - self.Q_table[s, a])
            s = self.state_list.pop(0)  # 将需要更新的状态动作从列表中删除,下次不必更新
            a = self.action_list.pop(0)
            self.reward_list.pop(0)
            # n步Sarsa的主要更新步骤
            self.Q_table[s, a] += self.alpha * (G - self.Q_table[s, a])
        if done:  # 如果到达终止状态,即将开始下一条序列,则将列表全清空
            self.state_list = []
            self.action_list = []
            self.reward_list = []

在悬崖漫步环境中运行 多步Sarsa 算法。

ncol = 12
nrow = 4
env = CliffWalkingEnv(ncol, nrow)
np.random.seed(0)
n_step = 5  # 5步Sarsa算法
alpha = 0.1
epsilon = 0.1
gamma = 0.9
agent = nstep_Sarsa(n_step, ncol, nrow, epsilon, alpha, gamma)
num_episodes = 500  # 智能体在环境中运行的序列的数量

return_list = []  # 记录每一条序列的回报
for i in range(10):  # 显示10个进度条
    #tqdm的进度条功能
    with tqdm(total=int(num_episodes / 10), desc='Iteration %d' % i) as pbar:
        for i_episode in range(int(num_episodes / 10)):  # 每个进度条的序列数
            episode_return = 0
            state = env.reset()
            action = agent.take_action(state)
            done = False
            while not done:
                next_state, reward, done = env.step(action)
                next_action = agent.take_action(next_state)
                episode_return += reward  # 这里回报的计算不进行折扣因子衰减
                agent.update(state, action, reward, next_state, next_action,
                             done)
                state = next_state
                action = next_action
            return_list.append(episode_return)
            if (i_episode + 1) % 10 == 0:  # 每10条序列打印一下这10条序列的平均回报
                pbar.set_postfix({
                    'episode':
                    '%d' % (num_episodes / 10 * i + i_episode + 1),
                    'return':
                    '%.3f' % np.mean(return_list[-10:])
                })
            pbar.update(1)

episodes_list = list(range(len(return_list)))
plt.plot(episodes_list, return_list)
plt.xlabel('Episodes')
plt.ylabel('Returns')
plt.title('5-step Sarsa on {}'.format('Cliff Walking'))
plt.show()

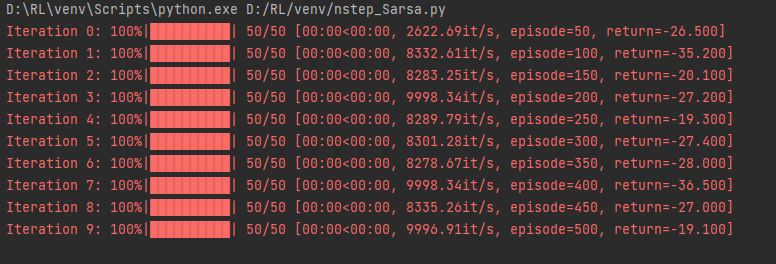
执行结果：

通过实验结果可以发现，多 步 Sarsa 算法的收敛速度比单步 Sarsa 算法更快。 

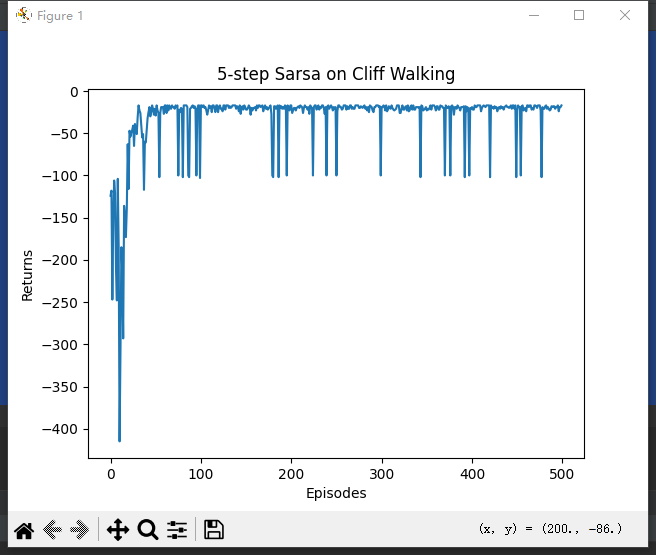
在通过代码看一下多步 Sarsa 算法得到的策略在各个状态下会使智能体采取什么样的动作，发现此时多步 Sarsa 算法得到的策略会在最远离悬崖的一边行走，以保证最大的安全性。

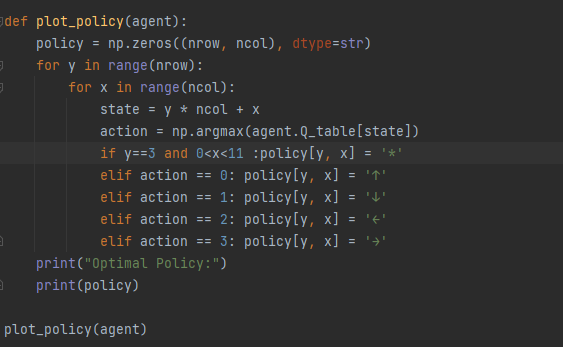
1.4 Q-learning 算法

        Q-Learning 是一种基于值的强化学习算法，借助 动作价值函数 Q ( s , a ) 来预估在给定状态 s下 采取动作 a 的期望回报。在更新时，Q-Learning 采用贪婪策略，即始终选取最大的 Q 值。

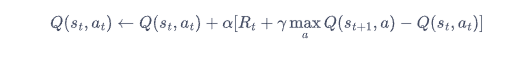
 a: 在新状态s’下具有最大Q值的动作

        当我们说 “max(Q(s’, a’))” 时，我们实际上是在选择在状态 s’ 下能够获得的最大Q值。也就是说，我们考虑所有可能的动作 a’，并找到其中具有最大Q值的那个动作。

        具体地说，Q-learning算法在每一步中，根据当前状态 s 以及在新状态 s’ 下的所有可能动作 a’ 的Q值，选择最大的Q值作为更新当前状态 s 和动作 a 的Q值。这意味着代理会选择当前策略中可能不会选择的动作，以便探索潜在的更好的策略。

 Q-learning 算法代码实践：

仍然在悬崖漫步环境下来实现 Q-learning 算法：

class QLearning:
    def __init__(self, ncol, nrow, epsilon, alpha, gamma, n_action=4):
        self.Q_table = np.zeros([nrow * ncol, n_action])  # 初始化Q(s,a)表格
        self.n_action = n_action  # 动作个数
        self.alpha = alpha  # 学习率
        self.gamma = gamma  # 折扣因子
        self.epsilon = epsilon  # epsilon-贪婪策略中的参数

    def take_action(self, state):  #选取下一步的操作
        if np.random.random() < self.epsilon:
            action = np.random.randint(self.n_action)
        else:
            action = np.argmax(self.Q_table[state])
        return action

    def best_action(self, state):  # 用于打印策略
        Q_max = np.max(self.Q_table[state])
        a = [0 for _ in range(self.n_action)]
        for i in range(self.n_action):
            if self.Q_table[state, i] == Q_max:
                a[i] = 1
        return a

    def update(self, s0, a0, r, s1):
        td_error = r + self.gamma * self.Q_table[s1].max() - self.Q_table[s0, a0]
        self.Q_table[s0, a0] += self.alpha * td_error

运行结果：

        在一个序列中 Sarsa 获得的期望回报是高于 Q-learning 的。因为在训练过程中智能体采取基于当前函数的-贪婪策略来平衡探索与利用，Q-learning 算法由于沿着悬崖边走，会以一定概率探索“掉入悬崖”这一动作，而 Sarsa 相对保守的路线使智能体几乎不可能掉入悬崖。

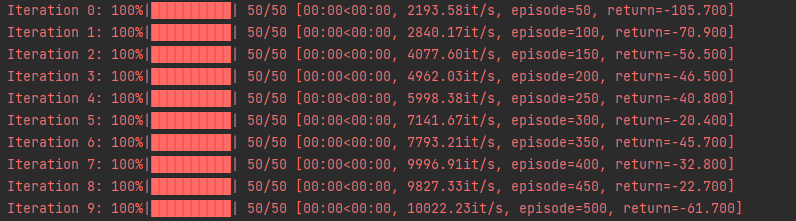
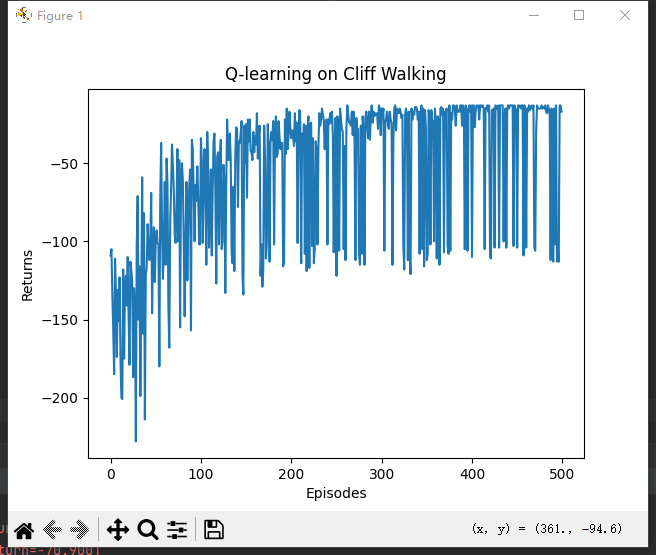
        把目标策略的行为打印出来后，发现其更偏向于走在悬崖边上，这与 Sarsa 算法得到的比较保守的策略相比是更优的。 

2 Dyna-Q算法 

        Q-planning 每次选取一个曾经访问过的状态 s，采取一个曾经在该状态下执行过的动作 a，通过模型得到转移后的状态  以及奖励 r ，并根据这个模拟数据(s,a,r,)，用 Q-learning 的更新方式来更新动作价值函数。

通过迷宫例子说明

3x3 迷宫：

• 真实交互：从 S 向右移动，到达空白格子，更新 Q(S, 右)。

• 模型记录：Model(S, 右) = (-1, 空白格子)。

规划阶段的模拟更新：

1. 随机选中历史中的 (S, 下)，模型返回 Model(S, 下) = (-10, X)。

   更新 Q(S, 下)，使其更负（即使你最近没有实际遇到陷阱 X，通过模拟历史数据，仍然能持续优化 Q(S, 下)，避免未来踩陷阱）。

2. 随机选中另一个历史 (空白格子, 左)，模型返回 (r, s')。

   更新 Q(空白格子, 左)，可能传播 S 方向的信息。

在 Dyna-Q 中如何让 Q(S, 下) 变得更负？

假设机器人已经有过以下真实交互：

• (S, 右) → 到达空白格子，奖励 -1。

• (S, 下) → 到达陷阱 X，奖励 -10。

• 假设：

  • 初始 Q(S,下)=0（未探索时通常初始化为 0）。

  • 学习率 α=0.1，折扣因子 γ=0.9。

  • 陷阱 XX 是终止状态，Q(X,∗)=0。

更新计算

1. 执行 (S, 下) 后：

   • 观测到 r=−10，下一状态 s′=X。

   • 计算 TD 目标：

     TD Target=r + γ*max⁡Q(X,a′)=−10+0.9×0=−10

   • TD 误差：

     TD Error=TD Target−Q(S,下)=−10−0=−10

   • 更新 Q(S,下)：

     Q(S,下)←Q(S,下)+α×TD Error=0+0.1×(−10)=−1

   • 第一次更新后，Q(S,下)=−1（仍然不够负，需要多次更新）。

2. 在 Dyna-Q 的规划阶段：

   • 随机采样到 (S, 下)，用模型查询：

     Model(S,下)→(r=−10,s′=X)

   • 再次用相同的 TD 更新：

     Q(S,下)←Q(S,下)+0.1×(−10−Q(S,下))

   • 如果当前 Q(S,下)=−1：

     Q(S,下)←−1+0.1×(−10−(−1))=−1+0.1×(−9)=−1−0.9=−1.9

   • 第二次更新后，Q(S,下)=−1.9（更负了）。

   • 重复多次后，Q(S,下)会趋近于真实值（约 -10）。

 

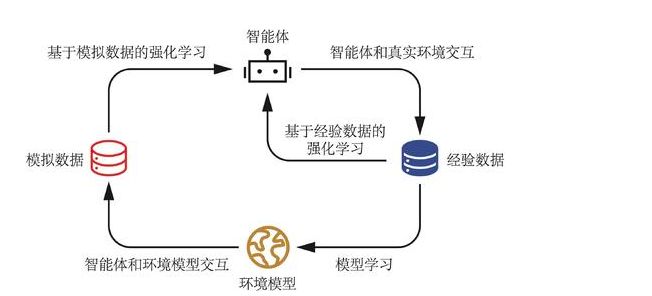
Dyna-Q算法只比Q-learning算法多一个步骤：Q-planing。Dyna-Q在正常的进行Q-learning更新Q值后，会把本次的数据 存进模型，然后进行多N次Q-planing。

Q-planing：随机选择一个曾经访问过的状态  和在在该状态下执行的动作  ，根据模型 M 获得在 ( ， )  时获得的奖励  和下一状态  ，紧接着使用(， ,  , )更新Q（，）。

Dyna-Q代码实践：

同样是在悬崖漫步环境下来实现Dyna-Q算法，输入参数是 Q-planning 的步数。若 Q-planning 步数为 0，Dyna-Q 算法则退化为 Q-learning。

def DynaQ_CliffWalking(n_planning):
    ncol = 12
    nrow = 4
    env = CliffWalkingEnv(ncol, nrow)
    epsilon = 0.01
    alpha = 0.1
    gamma = 0.9
    agent = DynaQ(ncol, nrow, epsilon, alpha, gamma, n_planning)
    num_episodes = 300  # 智能体在环境中运行多少条序列

    return_list = []  # 记录每一条序列的回报
    for i in range(10):  # 显示10个进度条
        # tqdm的进度条功能
        with tqdm(total=int(num_episodes / 10),
                  desc='Iteration %d' % i) as pbar:
            for i_episode in range(int(num_episodes / 10)):  # 每个进度条的序列数
                episode_return = 0
                state = env.reset()
                done = False
                while not done:
                    action = agent.take_action(state)
                    next_state, reward, done = env.step(action)
                    episode_return += reward  # 这里回报的计算不进行折扣因子衰减
                    agent.update(state, action, reward, next_state)
                    state = next_state
                return_list.append(episode_return)
                if (i_episode + 1) % 10 == 0:  # 每10条序列打印一下这10条序列的平均回报
                    pbar.set_postfix({
                        'episode':
                        '%d' % (num_episodes / 10 * i + i_episode + 1),
                        'return':
                        '%.3f' % np.mean(return_list[-10:])
                    })
                pbar.update(1)
    return return_list

np.random.seed(0)
random.seed(0)
n_planning_list = [0, 2, 20]
for n_planning in n_planning_list:
    print('Q-planning步数为：%d' % n_planning)
    time.sleep(0.5)
    return_list = DynaQ_CliffWalking(n_planning)
    episodes_list = list(range(len(return_list)))
    plt.plot(episodes_list,
             return_list,
             label=str(n_planning) + ' planning steps')
plt.legend()
plt.xlabel('Episodes')
plt.ylabel('Returns')
plt.title('Dyna-Q on {}'.format('Cliff Walking'))
plt.show()

运行结果：

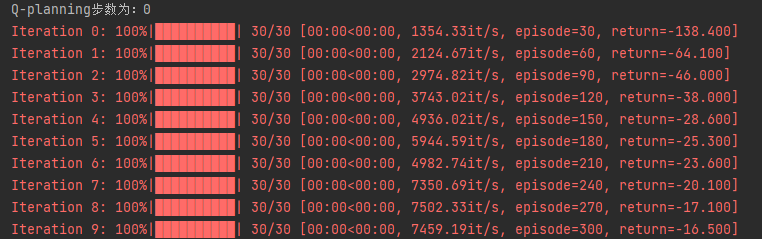
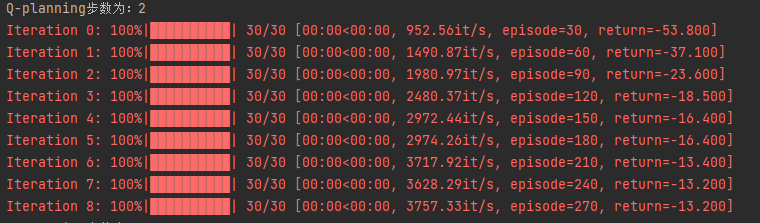
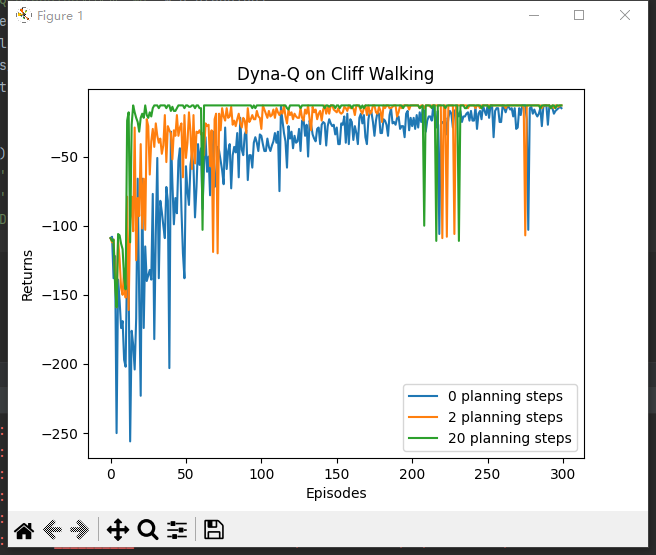
         从上述结果中我们可以很容易地看出，随着 Q-planning 步数的增多，Dyna-Q 算法的收敛速度也随之变快。当然，并不是在所有的环境中，都是 Q-planning 步数越大则算法收敛越快，这取决于环境是否是确定性的，以及环境模型的精度。在上述悬崖漫步环境中，状态的转移是完全确定性的，构建的环境模型的精度是最高的，所以可以通过增加 Q-planning 步数来直接降低算法的样本复杂度。