TOPSIS法

TOPSIS法

TOPSIS法(Technique for Order Preference by Similarity to ldeal Solution)

可翻译为逼近理想解排序法，国内常简称为优劣解距离法

TOPSIS法是一种常用的综合评价方法，其能充分利用原始数据的信息,

其结果能精确地反映各评价方案之间的差距。

在层次分析法的学习中,我们认识到了一些层次分析法的局限性,比如 n过大或者我们知道决策层中的指标数据,这种情况下层次分析法便不再适用,这种情况下我们应该在这么做呢

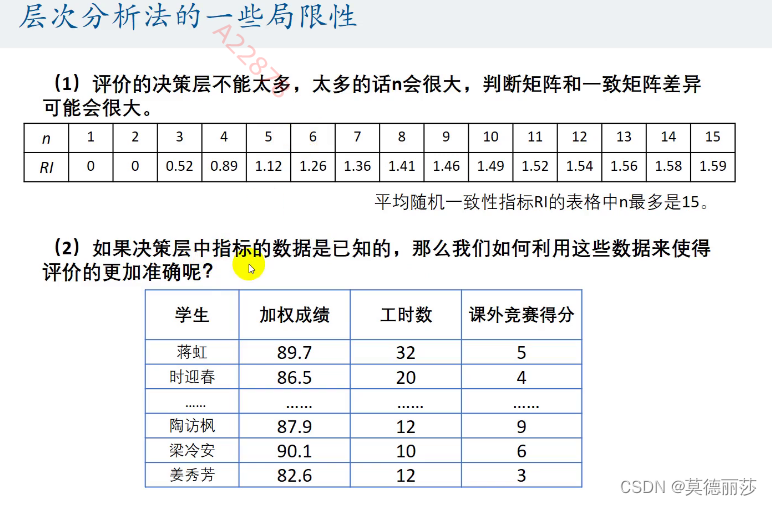
以下已知四个同学的成绩:

但是这种排名的方法仍然有不足的方法

这显然是不合理的

通过构造计算评分的方式,评分与成绩的关系更加密切了,因此评分相比上一种方法更加贴切这个例子

那为什么不直接用100分和0分作为上限和下限呢?

有以下几个点:

(1) 比较的对象一般要远大于两个。 (例如比较一个班级的成绩)

(2)比较的指标也往往不只是一-个方面的，例如成绩、工时数、课

外竞赛得分等。

(3)有很多指标不存在理论上的最大值和最小值，例如衡量经济增

长水平的指标: GDP增速。

但是在现实生活中,很多情况下指标的数量不止一个,在指标大于一个时我们该怎么样呢?

但是不同指标的类型也存在不同的地方,比如说有的指标越大越好,有的指标越小越好,在这里我们将其称作 极大型,极小型,不同类型的指标在计算中不能直接进行计算,这里一般通过将极小型转化为极大型的方法使其能够同时运算

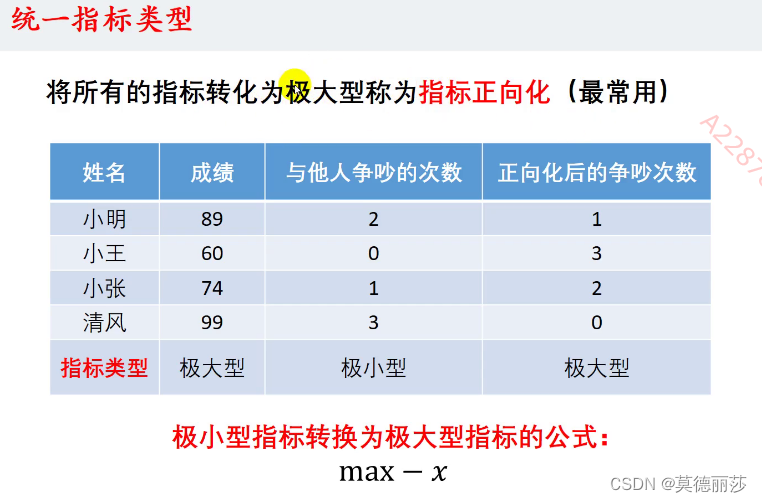
但是转换之后,虽然他们都是极大型指标,但是他们的量纲不同,(即每个单位指标对结果的影响不同),所以这时我们应该对他们进行标准化处理

比如这里,成绩的1分以及争吵次数的一次,显然对结果的影响不同,这样就会对结果的准确性带来不小的影响

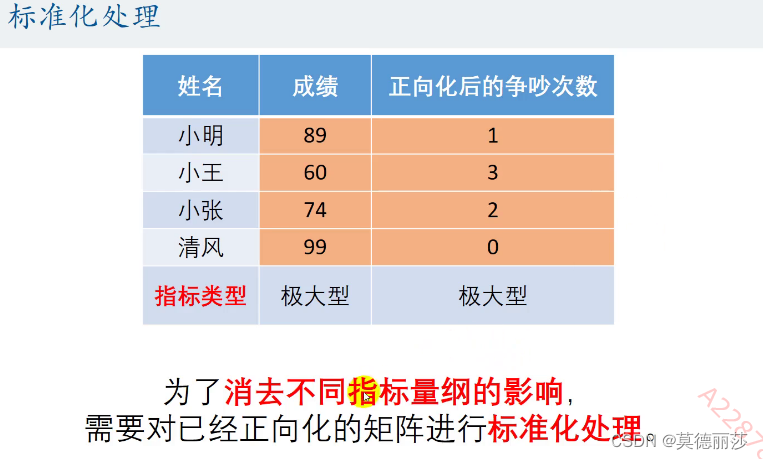
用以上方法将例子中的两个指标标准化后我们得到:

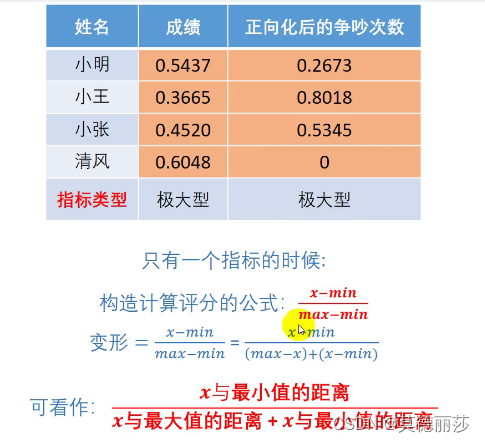
计算得分

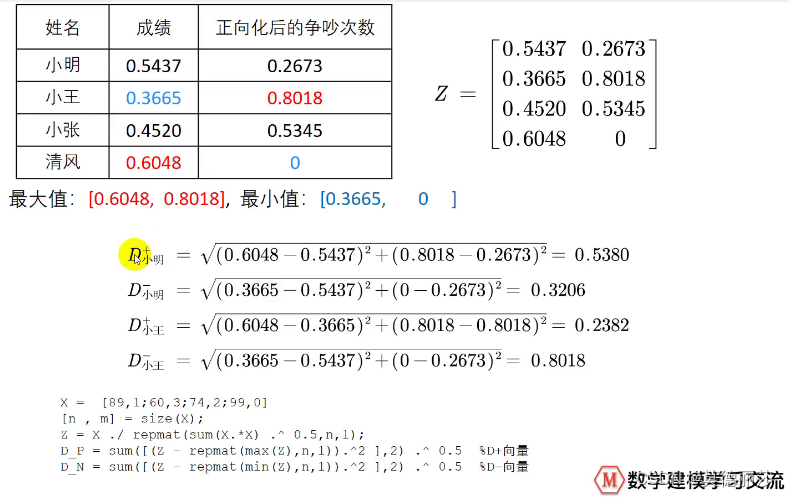
对两个指标进行综合考虑后,我们得到得分如下

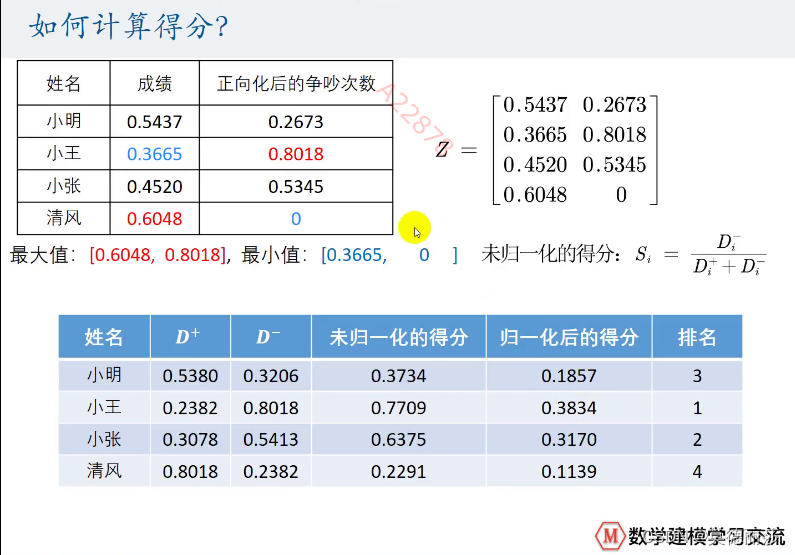
TOPSIS法的使用方法

一.正向化

以上我们介绍了极大型和极小型指标,还有中间性指标和区间型指标总共四种常见指标:

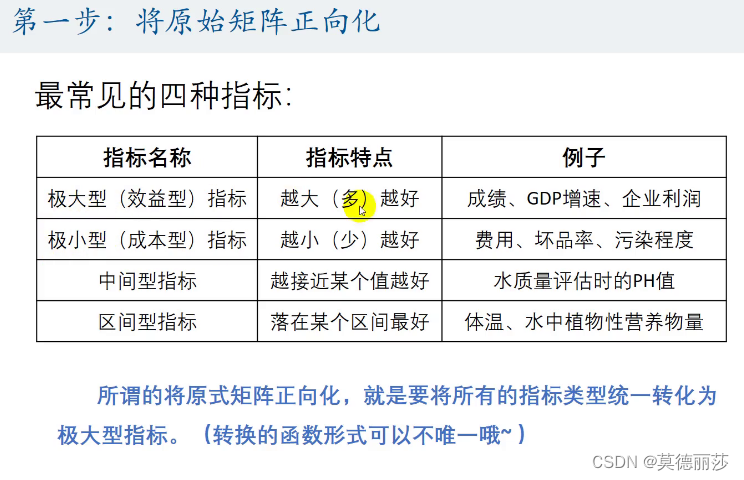
不同类型指标之间的转化方式:

1.极小型→极大型

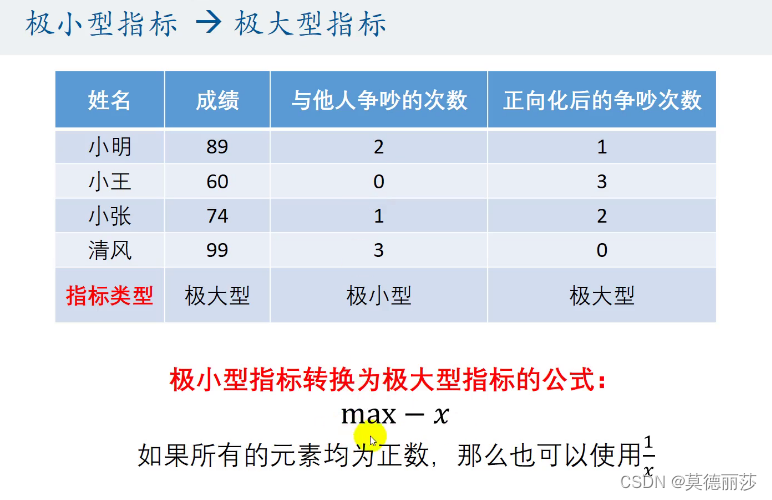
2.中间型→极大型

3.区间型→极大型

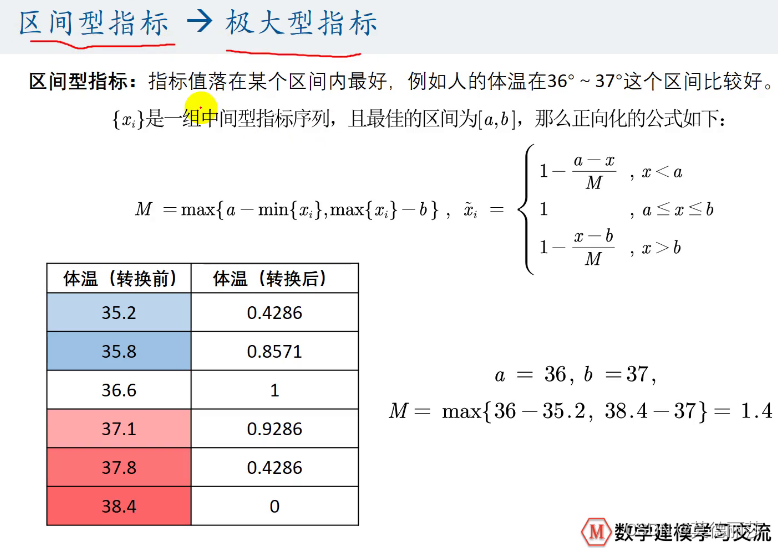
二.标准化

标准化的作用是消除量纲的影响

三.计算得分并归一化

计算得分

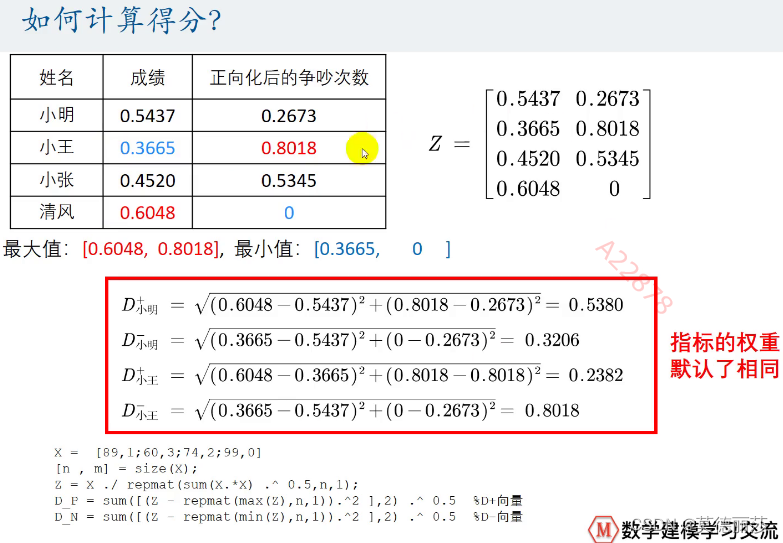
在这里,我们默认不同指标之间的权重相同,但是实际情况中,不同的指标的影响程度大部分情况下都是不一样的,故有需要我们需要根据不同指标的重要程度对他们选择使用不同的权重

练习:

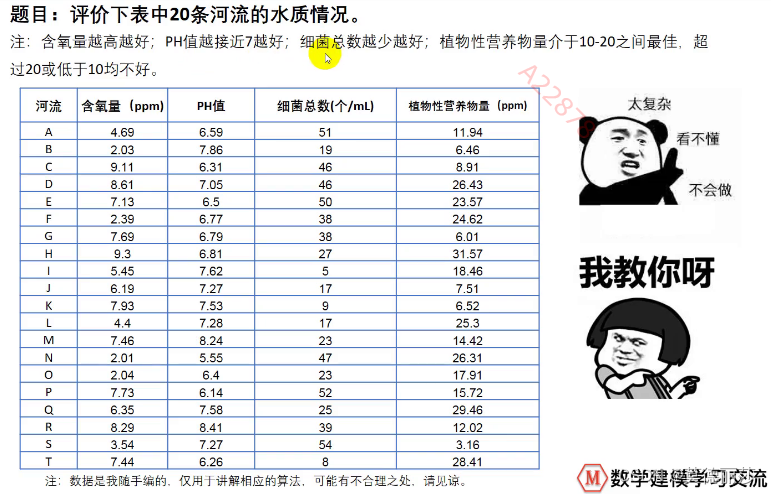
在此题目中,含氧量是极大型指标,ph是中间型指标,细菌总数是极小型指标,营养物质为去践行指标

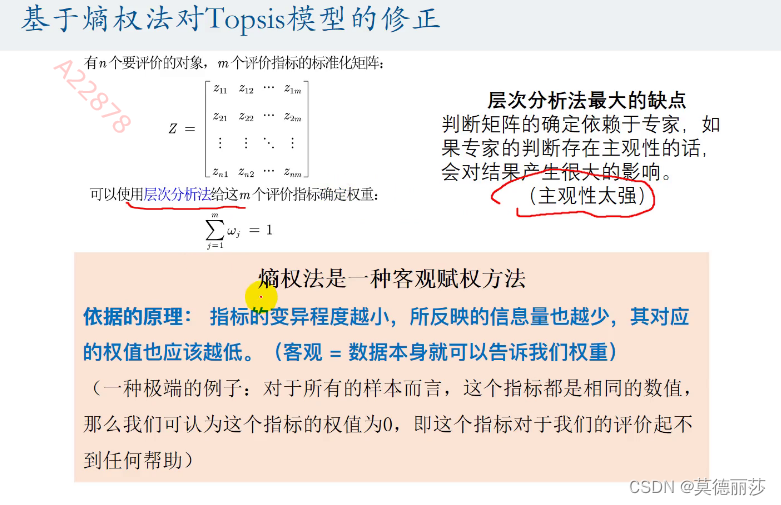
基于熵权法对TOPSIS模型的修正

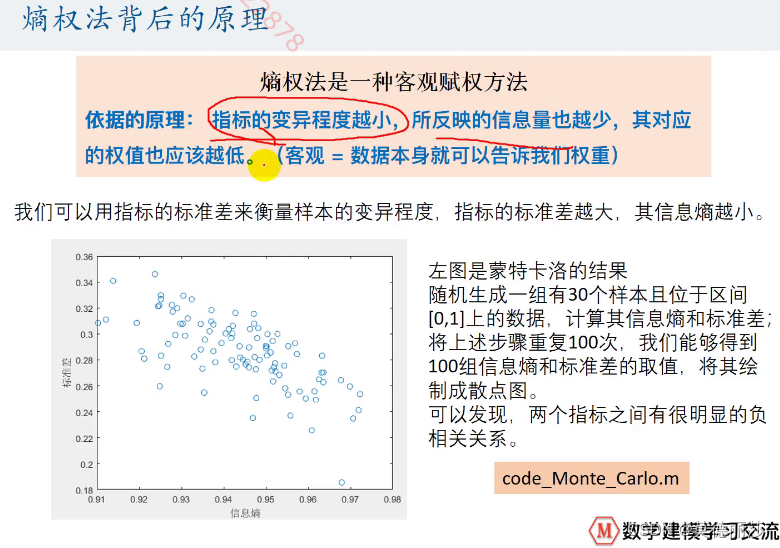
熵权法是一种了客观赋权的方法

这里的变异程度指方差,即对结果的影响程度,根据影响程度的大小对指标进行赋权

阅读以下案例

我们得到结果: 越有可能发生的事情信息量越少,越不可能发生的事情信息量越多。

我们可以将这种思路使用函数拟合出来,并可以得到如下关系

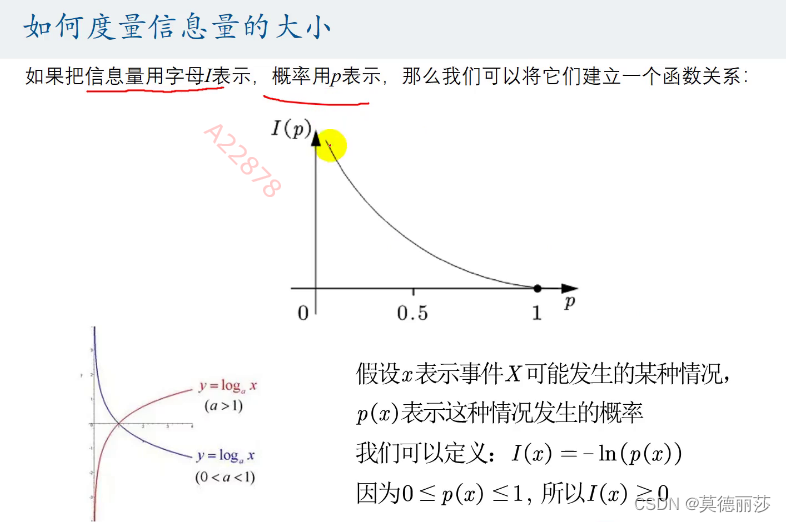
这件事情发生的概率设作p(x)

所以信息熵我们可以设作I(x) = -ln(p(x))

信息熵越大,则他的值能给你补充的信息量越大,而知道这个值前你已有的信息总量越小。

熵权法的计算步骤

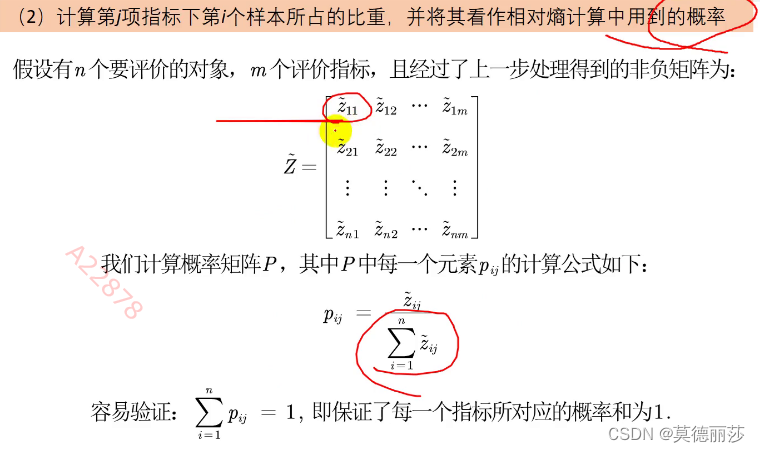
指标的变异程度,也就是标准差,我们根据这个特征对指标进行连接