矩阵的幂
矩阵的幂是指将一个矩阵自身相乘多次的操作。具体来说,如果 A 是一个 n×n 的方阵,那么 A 的 k 次幂 A^k 定义为 A 自身相乘 k 次的结果。
设 A 是一个 n×n 的方阵,那么 A 的 k 次幂 A^k 定义为:
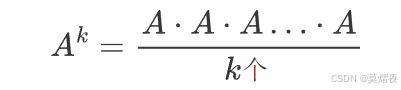
其中 k 是一个正整数。
性质
矩阵幂具有以下性质:
-
结合律:对于任意正整数 k 和 l,

-
分配律:对于任意正整数 k 和 l,

(除非 A 和 B 是可交换的)例如A+B的平方:

如果A和B可交换,则AB=BA,所以

如果A和B不可交换,则AB与BA不等,则上述公式不能合并为2AB。
-
单位矩阵:对于任意方阵A,A^0=E,其中 E 是单位矩阵。
矩阵的转置
矩阵的转置(Transpose)是矩阵操作中的一种基本运算。它通过交换矩阵的行和列来生成一个新的矩阵。具体来说,如果 A 是一个
m×n 的矩阵,那么它的转置矩阵 A^T 是一个 n×m 的矩阵,其中 A^T 的第 i 行第 j 列的元素等于 A 的第 j 行第i 列的元素。
定义
设 A 是一个 m×n 的矩阵,其元素为 aij,那么 A 的转置矩阵 A^T 是一个 n×m 的矩阵,其元素为 aji。
性质
矩阵转置具有以下性质:
-
(A^T)^T = A:一个矩阵的转置的转置等于原矩阵。
-
(A + B)^T = A^T + B^T:两个矩阵和的转置等于它们各自转置的和。
-
(kA)^T = kA^T:一个矩阵乘以一个标量的转置等于该矩阵的转置乘以该标量。
-
(AB)^T = B^T A^T:两个矩阵乘积的转置等于它们各自转置的乘积,但顺序相反。
特殊矩阵
-
对称矩阵:如果一个矩阵 A 满足 A^T=A,那么 A 是对称矩阵。对称矩阵的元素关于主对角线对称。
如:

-
反对称矩阵:如果一个矩阵 A 满足 A^T=−A,那么 A 是反对称矩阵。反对称矩阵的主对角线元素必须为零,且关于主对角线对称的元素互为相反数。
如:

反对称矩阵:

所以:
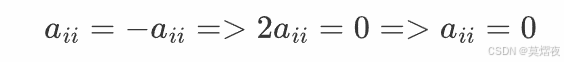
得出主对角线元素必须为零。
对称矩阵和反对称矩阵都是方阵。
矩阵A和B为同阶对称矩阵,AB对称的充要条件为AB=BA
方阵的行列式
要计算行列式的前提为矩阵A为方阵。
性质:A为n阶的方阵

伴随矩阵
设 A 是一个 n×n 的方阵,其元素为 aij。伴随矩阵 adj(A)或A* 是一个 n×n的矩阵,其第 i 行第 j 列的元素是 A 的余子式 Mji 的代数余子式 Cji,即:

其中 Mji是 A 的第j 行第i 列元素的余子式,即去掉第 j 行和第 i 列后剩下的 (n−1)×(n−1) 矩阵的行列式。
简单理解:
1.先按行求出每个元素的代数余子式
2.将每行元素的代数余子式按列组成一个矩阵,该矩阵就是伴随矩阵。
性质1:

性质2:

逆矩阵
对于一个 n×n 的方阵 A,如果存在另一个 n×n的方阵 B,使得 AB=BA=E,其中 E 是 n×n 的单位矩阵,那么 B 称为 A 的逆矩阵,记作

逆矩阵的存在条件
一个矩阵 A 有逆矩阵的充分必要条件是 A 是可逆的,即 det(A)≠0。如果 det(A)=0,则 A 是奇异矩阵,没有逆矩阵。
思考:如果A可逆,则可逆矩阵是唯一的
证明:
假设可逆矩阵不是唯一的,存在两个可逆矩阵B1和B2,则由可逆矩阵定义可知:

则:

所以可逆矩阵唯一。
性质:
1.n阶方阵A可逆的充要条件为
![]()
且当A可逆时,

初等变换
初等变换一般可以分为两种类型:行变换、列变换。
初等行变换:
-
交换两行:将矩阵的第 i 行和第 j 行交换位置
如:矩阵第二行和第三行交换

-
某一行乘以非零常数:将矩阵的第i 行乘以一个非零常数 k
如:第二行乘以非零整数k

-
某一行加上另一行的倍数:将矩阵的第 i行加上第 j 行的 k 倍
如:矩阵第一行乘以-4加到第二行

初等列变换
-
交换两列:将矩阵的第 i 列和第 j 列交换位置
-
某一列乘以非零常数:将矩阵的第 i 列乘以一个非零常数 k
-
某一列加上另一列的倍数:将矩阵的第 i 列加上第 j 列的 k 倍
矩阵的标准形
常见的矩阵标准形包括行阶梯形矩阵、简化行阶梯形矩阵等。
行阶梯形矩阵
行阶梯形矩阵是一种特殊的矩阵形式,具有以下特征:
-
非零行在零行之上:所有非零行都在零行之上。
-
主元:每一行的第一个非零元素(主元)在上一行主元的右边。
-
主元下方元素为零:每一行的主元下方元素都为零。
简化行阶梯形矩阵
简化行阶梯形矩阵是行阶梯形矩阵的一种特殊形式,具有以下特征:
-
非零行在零行之上:所有非零行都在零行之上。
-
主元为 1:每一行的第一个非零元素(主元)为 1。
-
主元下方元素为零:每一行的主元下方元素都为零。
-
主元上方元素为零:每一行的主元上方元素都为零。
即:
1.是行阶梯形矩阵;2.非0行的首非0元是1;3.非0行的首非0元所在列的其它元素都是0
向量
定义
向量可以用多种方式定义,以下是几种常见的定义:
-
几何定义:向量是一个有方向和大小的量,通常用箭头表示。向量的起点称为原点,终点称为向量的端点。
-
代数定义:向量是一个有序的数组,通常表示为列向量或行向量。
例如,一个 n 维列向量可以表示为:

一个 n 维行向量可以表示为:

其中 v1,v2,…,vn是向量的分量。
行向量和列向量再本质上没有区别。
向量的表示
向量可以用多种方式表示,以下是几种常见的表示方法:
-
几何表示:在二维或三维空间中,向量通常用箭头表示,箭头的方向表示向量的方向,箭头的长度表示向量的大小。
-
代数表示:向量可以用列向量或行向量表示,如上所述。
-
坐标表示:在二维或三维空间中,向量可以用坐标表示。例如,二维向量 v=(v1,v2)v=(v1,v2) 表示在 xx 轴和 yy 轴上的分量。
向量的运算
向量有几种基本的运算,包括加法、数乘、点积和叉积。
向量加法
向量加法是将两个向量的对应分量相加,得到一个新的向量。例如,两个 n 维向量 u 和 v 的加法为:

向量数乘
向量数乘是将一个向量的每个分量乘以一个标量,得到一个新的向量。例如,一个 n 维向量 v 与标量 k 的数乘为:

向量点积
向量点积(内积)是将两个向量的对应分量相乘,然后将结果相加,得到一个标量。例如,两个 n 维向量 u 和 v 的点积为:

矩阵的特征值和特征向量
定义
设 A 是一个 n×n 的方阵。如果存在一个非零列向量 v 和一个标量 λ,使得:
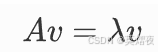
那么 λ 称为矩阵 A的特征值,v 称为对应于特征值 λ 的特征向量。
注:λ可以为0,而v不能为0,并且v是列向量。因为A是n维矩阵,如果v是行向量,则维数是1xn,不满足矩阵相乘。
将定义中的等式移项,得到:

由于v是非零列向量,相当于求上述方程的非零解,由方程有非零解的充要条件是行列式为0的定理可知:
![]()
说明:(A-λE):特征矩阵;|A-λE|:特征行列式或特征多项式;|A-λE|=0:特征方程
结论:
1.λ是A的特征值,v是对应λ的一个特征向量,则cv也是λ的一个特征向量,c为不等于0的标量。
根据定义:

等式两边同乘以c
![]()
所以cv也是λ的一个特征向量。
向量的模
定义
向量 v 的模记作 ∥v∥,计算公式为:

几何解释
在二维空间中,向量 v=(v1,v2)的模表示从原点到点 (v1,v2)的距离。在三维空间中,向量 v=(v1,v2,v3)的模表示从原点到点 (v1,v2,v3)的距离。
||v||=1,叫做单位向量的模。如:v=(1,0,0)
性质
-
非负性:∥v∥≥0,并且 ∥v∥=0 当且仅当 v=0(零向量)。
-
齐次性:对于任意标量 k,∥kv∥=∣k∣∥v∥。
-
三角不等式:对于任意向量 u 和 v,∥u+v∥≤∥u∥+∥v∥。
向量的内积
定义
对于两个 n 维向量 a=(a1,a2,…,an) 和 b=(b1,b2,…,bn),它们的内积(点积)表示为 a⋅b,计算公式为:

几何解释
在几何上,内积也可以通过向量的模和它们之间的夹角来表示。具体来说,如果 θ 是向量 a 和 b 之间的夹角,那么内积可以表示为:

其中:
-
∥a∥ 和 ∥b∥ 分别是向量 a 和 b 的模(长度)。
-
cos(θ)是夹角 θ 的余弦值。
性质
-
交换律:a⋅b=b⋅a
-
分配律:a⋅(b+c)=a⋅b+a⋅c
-
数乘结合律:(ka)⋅b=k(a⋅b)=a⋅(kb)(,其中 k 是标量。
-
正定性:a⋅a≥0,并且 a⋅a=0 当且仅当 a=0。
向量内积的几何解释其实就是余弦相似度算法的公式,当cos(θ)=1时,表示两个向量重合;当cos(θ)=0时,表示两个向量垂直。
如果使用两个向量分别近似表示两个文本或图像,两个向量的cos(θ)越接近1,表示这两个文本内容越相似,cos(θ)越接近0,表示这两个文本内容越不相似。
向量的余弦公式是

其中a,b是向量,余弦也叫余弦函数,是三角函数的一种,且余弦定理亦称第二余弦定理,是关于三角形边角关系的重要定理之一。
使用余弦相似度计算两段文本的相似度
安装jieba库
pip install jieba
import jieba
import re
from math import sqrt
def cosine_similarity(vec1, vec2):
"""计算两个向量的余弦相似度"""
dot_product = sum(p*q for p,q in zip(vec1, vec2))
magnitude1 = sqrt(sum([val**2 for val in vec1]))
magnitude2 = sqrt(sum([val**2 for val in vec2]))
if not magnitude1 or not magnitude2:
return 0
return dot_product / (magnitude1 * magnitude2)
def preprocess_text(text):
"""预处理文本,移除非汉字字符"""
return re.sub(r'[^\u4e00-\u9fa5]', '', text)
def text_to_vector(text):
"""将文本转换成词频向量"""
words = set(' '.join(lists).split())
return words
def calculate_similarity(s1, s2):
# 预处理文本
s1 = preprocess_text(s1)
s2 = preprocess_text(s2)
# 使用jieba进行分词
listA = list(jieba.cut(s1))
listB = list(jieba.cut(s2))
# 创建词汇集合
word_set = set(listA).union(set(listB))
# 计算词频向量
freq_listA = [listA.count(word) for word in word_set]
freq_listB = [listB.count(word) for word in word_set]
# 计算余弦相似度
return cosine_similarity(freq_listA, freq_listB)
if __name__ == "__main__":
s1 = "这只皮靴号码大了。那只号码合适"
s2 = "这只皮靴号码不小,那只更合适"
similarity = calculate_similarity(s1, s2)
print(f"文本相似度为: {similarity}")
首先添加一个preprocess_text函数用于去除字符串中的非汉字字符。这里使用的正则表达式[^\u4e00-\u9fa5]匹配所有非汉字字符,并通过re.sub函数替换为空字符串,从而达到清理文本的目的。然后定义一个计算余弦相似度的函数cosine_similarity,然后定义一个将文本转换成词频向量的函数text_to_vector),以及主要的计算相似度的函数calculate_similarity。























 6124
6124

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








