利用主定理求分治算法的渐进时间复杂度

主定理的英文是Master theorem。

主定理常常被用于求分治算法的时间复杂度。分治算法就是将一个主问题分解成若干个规模相似的子问题。

一个分治算法的运行时间可用一条递归关系式表示为

其中T(n)表示问题规模为n的分治算法所需的运行时间。a 表示在每个递归级别创建的子问题的数量。n/b表示一个规模为n的主问题被分解为规模为n/b的子问题。f(n)表示创建子问题并将其结果合并到上述过程中的时间。

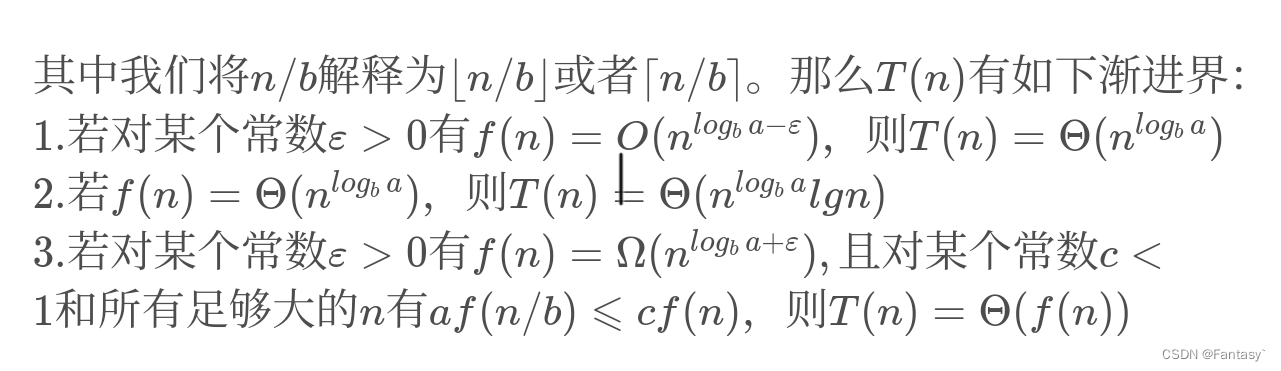
如（该问题来自于MIT6.006）

给定一个一维的数组a，其中存放了n个int型整数。

peak的定义为当(i != 0或 i != n-1)时，a[i] >= a[i-1] && a[i] >= a[i+1]；当i == 0时a[i] >= a[i+1]；当i==n-1时，a[i] >= a[i-1]。

请设计一个算法，找到这串整数的一个peak。

可以使用二分法来解决。

当a[n/2] < a[n/2-1]时，找a[0:n/2-1]；当a[n/2] < a[n/2+1]时，找a[n/2+1:n-1]；当以上两个条件都不满足时，说明a[n/2]这个元素为peak。

对于这样的二分法，我们可以通过主定理求其时间复杂度。