java学习 73矩阵置零 54螺旋矩阵 148排序链表

返校开始新一轮的学习，加油

73矩阵置零

public class Solution {
    public void setZeroes(int[][] matrix) {
        if (matrix == null || matrix.length == 0 || matrix[0].length == 0) {
            return;
        }
        
        int m = matrix.length;
        int n = matrix[0].length;
        
        // 标记第一行和第一列是否需要被置零
        boolean firstRowZero = false;
        boolean firstColZero = false;
        
        // 检查第一行是否有 0
        for (int j = 0; j < n; j++) {
            if (matrix[0][j] == 0) {
                firstRowZero = true;
                break;
            }
        }
        
        // 检查第一列是否有 0
        for (int i = 0; i < m; i++) {
            if (matrix[i][0] == 0) {
                firstColZero = true;
                break;
            }
        }
        
        // 遍历矩阵（从 [1,1] 开始），使用第一行和第一列作为标记
        for (int i = 1; i < m; i++) {
            for (int j = 1; j < n; j++) {
                if (matrix[i][j] == 0) {
                    matrix[i][0] = 0; // 标记第 i 行需要置零
                    matrix[0][j] = 0; // 标记第 j 列需要置零
                }
            }
        }
        
        // 根据第一行的标记，将对应的列置零
        for (int j = 1; j < n; j++) {
            if (matrix[0][j] == 0) {
                for (int i = 1; i < m; i++) {
                    matrix[i][j] = 0;
                }
            }
        }
        
        // 根据第一列的标记，将对应的行置零
        for (int i = 1; i < m; i++) {
            if (matrix[i][0] == 0) {
                for (int j = 1; j < n; j++) {
                    matrix[i][j] = 0;
                }
            }
        }
        
        // 如果第一行原本有 0，则将第一行全部置零
        if (firstRowZero) {
            for (int j = 0; j < n; j++) {
                matrix[0][j] = 0;
            }
        }
        
        // 如果第一列原本有 0，则将第一列全部置零
        if (firstColZero) {
            for (int i = 0; i < m; i++) {
                matrix[i][0] = 0;
            }
        }
    }
}

示例，先把第0行0列做标记，然后遍历[1,1]以后的，把它对应的0行和0列元素打上标记，最后统一处理0行，0列，注意先后顺序 

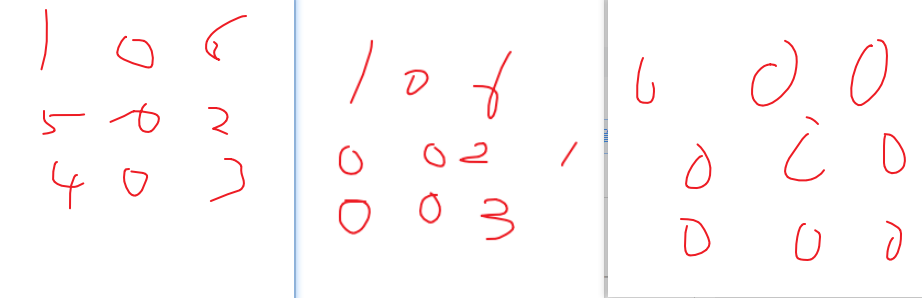
54螺旋矩阵

public class Solution {
    public void setZeroes(int[][] matrix) {
        if (matrix == null || matrix.length == 0 || matrix[0].length == 0) {
            return;
        }
        
        int m = matrix.length;
        int n = matrix[0].length;
        
        // 标记第一行和第一列是否需要被置零
        boolean firstRowZero = false;
        boolean firstColZero = false;
        
        // 检查第一行是否有 0
        for (int j = 0; j < n; j++) {
            if (matrix[0][j] == 0) {
                firstRowZero = true;
                break;
            }
        }
        
        // 检查第一列是否有 0
        for (int i = 0; i < m; i++) {
            if (matrix[i][0] == 0) {
                firstColZero = true;
                break;
            }
        }
        
        // 遍历矩阵（从 [1,1] 开始），使用第一行和第一列作为标记
        for (int i = 1; i < m; i++) {
            for (int j = 1; j < n; j++) {
                if (matrix[i][j] == 0) {
                    matrix[i][0] = 0; // 标记第 i 行需要置零
                    matrix[0][j] = 0; // 标记第 j 列需要置零
                }
            }
        }
        
        // 根据第一行的标记，将对应的列置零
        for (int j = 1; j < n; j++) {
            if (matrix[0][j] == 0) {
                for (int i = 1; i < m; i++) {
                    matrix[i][j] = 0;
                }
            }
        }
        
        // 根据第一列的标记，将对应的行置零
        for (int i = 1; i < m; i++) {
            if (matrix[i][0] == 0) {
                for (int j = 1; j < n; j++) {
                    matrix[i][j] = 0;
                }
            }
        }
        
        // 如果第一行原本有 0，则将第一行全部置零
        if (firstRowZero) {
            for (int j = 0; j < n; j++) {
                matrix[0][j] = 0;
            }
        }
        
        // 如果第一列原本有 0，则将第一列全部置零
        if (firstColZero) {
            for (int i = 0; i < m; i++) {
                matrix[i][0] = 0;
            }
        }
    }
}

 注意：维护上下左右边界， 在执行“从右到左”和“从下到上”这两个步骤前，需要检查 top <= bottom 和 left <= right 是否仍然成立，因为前两步可能已经改变了边界，导致这两步不再需要执行（例如，只剩一行或一列时）。

 148排序链表

/**
 * Definition for singly-linked list.
 * public class ListNode {
 *     int val;
 *     ListNode next;
 *     ListNode() {}
 *     ListNode(int val) { this.val = val; }
 *     ListNode(int val, ListNode next) { this.val = val; this.next = next; }
 * }
 */
class Solution {
    public ListNode sortList(ListNode head) {
        

if(head == null || head.next == null){
    return head;
}

ListNode slow = head;
ListNode fast = head;
ListNode prev = null;

while(fast != null && fast.next !=null){
    prev = slow;
    slow = slow.next;
    fast = fast.next.next;

}

prev.next = null;

ListNode left = sortList(head);
ListNode right = sortList(slow);
return merge(left,right);





  
        
    }


    



private ListNode merge(ListNode l1,ListNode l2){
ListNode dummy = new ListNode(0);
ListNode current = dummy;
    while(l1!= null && l2 !=null){
          if(l1.val<=l2.val){
        current.next = l1;
        l1 = l1.next;
    }else{
        current.next = l2;
        l2 = l2.next;

    }
    current = current.next;

}
current.next = (l1 != null)?l1:l2;
return dummy.next;

    }
}