信息学奥赛一本通|1338：【例3-3】医院设置

1338：【例3-3】医院设置

时间限制: 1000 ms 内存限制: 65536 KB
提交数: 6449 通过数: 4362

【题目描述】

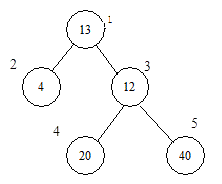
设有一棵二叉树（如下图），其中圈中的数字表示结点中居民的人口，圈边上数字表示结点编号。现在要求在某个结点上建立一个医院，使所有居民所走的路程之和为最小，同时约定，相邻结点之间的距离为1。就本图而言，若医院建在1处，则距离和=4+12+2×20+2×40=136；若医院建在3处，则距离和=4×2+13+20+40=81……

【输入】

第一行一个整数n，表示树的结点数（n≤100）。接下来的n行每行描述了一个结点的状况，包含三个整数，整数之间用空格（一个或多个）分隔，其中：第一个数为居民人口数；第二个数为左链接，为0表示无链接；第三个数为右链接，为0表示无链接。

【输出】

一个整数，表示最小距离和。

【输入样例】

5 
13 2 3
4 0 0 
12 4 5 
20 0 0 
40 0 0

【输出样例】

81

【算法分析】

这是一道简单的二叉树应用问题，问题中的结点数并不多，数据规模也不大，采用邻接矩阵存储，用Floyed法求出任意两结点之间的最短路径长，然后穷举医院可能建立的n个结点位置，找出一个最小距离的位置即可。当然也可以用双链表结构或带父结点信息的数组存储结构来解决，但实际操作稍微麻烦了一点。

【代码】

#include<iostream>
#include<cstdio>
using namespace std;
int a[101];		//用于存放每个结点的人口数
int g[101][101];//用于存放两结点间的最短路径
int main()
{
	int n,min=100000000,tot,l,r;	//l、r分别表示左右孩子2
	cin>>n;							//输入总结点数
	for(int i=1;i<=n;i++)
		for(int j=1;j<=n;j++)
			g[i][j]=1000000;		//初始化任意两结点间的最短路径为无穷大
	for(int i=1;i<=n;i++)
	{
		g[i][i]=0;					//不考虑自身到自身的路径，初始化为0
		cin>>a[i]>>l>>r;			//输入各结点的人口数、左右孩子
		if(l>0) g[i][l]=g[l][i]=1;	//如果有孩子，则与孩子的路径设为1
		if(r>0) g[i][r]=g[r][i]=1;
	}
    //Floyed算法求任意两节点间的最短路径
	for(int k=1;k<=n;k++)			//依次加入每个新结点，对最短路径进行更新
		for(int i=1;i<=n;i++)
		if(i!=k)
			for(int j=1;j<=n;j++)
			if(i!=j&&k!=j&&g[i][k]+g[k][j]<g[i][j])
				g[i][j]=g[i][k]+g[k][j];
	for(int i=1;i<=n;i++)			//枚举医院建在n个节点，找出最小距离和
	{
		tot=0;
		for(int j=1;j<=n;j++)
			tot+=g[i][j]*a[j];
		if(tot<min)   min=tot;
	}
	cout<<min;
	return 0;
}