（注：为黑马教学笔记整理，用以自用，如有条件，请支持正版教学）
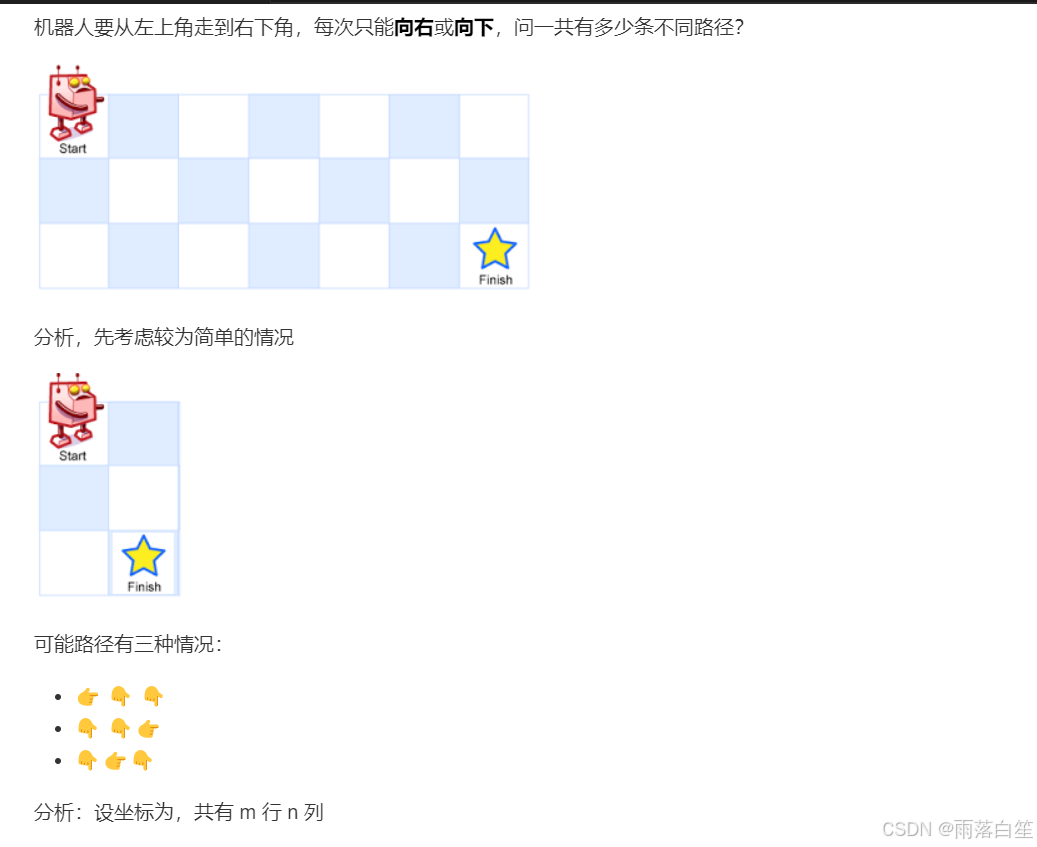
起始：不同路径
(0,0) (0,1)
(1,0) (1,1)
(2,0) (2,1)
如果终点是 (0,1) 那么只有一种走法
如果终点是 (1,0) 那么也只有一种走法
如果终点是 (1,1) 呢，它的走法是从它的上方走下来，或者从它的左边走过来，因此走法 = (0,1) + (1,0) = 2种
如果终点是 (2,0) 那么也只有一种走法
如果终点是 (2,1) 呢，它的走法是从它的上方走下来，或者从它的左边走过来，因此走法 = (1,1) + (2,0) = 3种
总结规律发现：
终点是 (0,1) (0,2) (0,3) … (0,n) 走法只有1种
终点是 (1,0) (2,0) (3,0) … (m,0) 走法也只有1种
除了上面两种情况以外，(i,j) 处的走法等于(i-1,j) + (i,j-1) 的走法之和，即为递推公式
画表格
0 1 1 1 1 1 1
1 2 3 4 5 6 7
1 3 6 10 15 21 28
题解
public class UniquePaths {
public static void main(String[] args) {
int count = new UniquePaths().uniquePaths(3, 7);
System.out.println(count);
}
public int uniquePaths(int m, int n) {
int[][] dp = new int[m][n];
for (int i = 0; i < m; i++) {
dp[i][0] = 1;
}
for (int j = 0; j < n; j++) {
dp[0][j] = 1;
}
for (int i = 1; i < m; i++) {
for (int j = 1; j < n; j++) {
dp[i][j] = dp[i - 1][j] + dp[i][j - 1];
}
}
return dp[m - 1][n - 1];
}
}
降维
public class UniquePaths {
public static void main(String[] args) {
int count = new UniquePaths().uniquePaths(3, 7);
System.out.println(count);
}
public int uniquePaths(int m, int n) {
int[] dp = new int[n];
Arrays.fill(dp, 1);
for (int i = 1; i < m; i++) {
dp[0] = 1;
for (int j = 1; j < n; j++) {
dp[j] = dp[j] + dp[j - 1];
}
}
return dp[n - 1];
}
}
分析
这个代码是解决一个经典的动态规划问题，称为“不同路径问题”（Unique Paths Problem）。问题描述如下：
问题描述
给定一个 m x n 的网格（grid），一个机器人位于左上角 (0, 0)，需要移动到右下角 (m-1, n-1)。机器人只能向右或者向下移动。问机器人有多少种不同的路径到达右下角。
解题思路
这个问题可以通过动态规划来求解。动态规划的基本思路是将问题分解为更小的子问题，通过存储子问题的解来避免重复计算。
动态规划的基本步骤
-
定义状态：
- 使用一个二维数组
dp来表示状态，其中dp[i][j]表示机器人从左上角(0, 0)移动到位置(i, j)的不同路径数量。
- 使用一个二维数组
-
状态转移方程：
- 对于位置
(i, j)，机器人可以从上方位置(i-1, j)或左方位置(i, j-1)移动过来。因此，dp[i][j]的值等于来自上方的路径数量加上来自左方的路径数量：
[
dp[i][j] = dp[i-1][j] + dp[i][j-1]
]
- 对于位置
-
初始化：
- 对于最左边的第一列
dp[i][0]，机器人只能一直向下移动到达该列，所以所有的dp[i][0]初始化为1。 - 对于最上边的第一行
dp[0][j]，机器人只能一直向右移动到达该行，所以所有的dp[0][j]初始化为1。
- 对于最左边的第一列
-
计算最终结果：
- 根据状态转移方程从上到下、从左到右逐步计算出每个位置的路径数量，最终
dp[m-1][n-1]就是从(0, 0)到(m-1, n-1)的不同路径数量。
- 根据状态转移方程从上到下、从左到右逐步计算出每个位置的路径数量，最终
代码解析
public class UniquePaths {
public static void main(String[] args) {
int count = new UniquePaths().uniquePaths(3, 7);
System.out.println(count);
}
public int uniquePaths(int m, int n) {
int[][] dp = new int[m][n]; // 创建一个二维数组来保存路径数量
// 初始化第一列，机器人只能一直向下走，所以每个格子路径数量为1
for (int i = 0; i < m; i++) {
dp[i][0] = 1;
}
// 初始化第一行，机器人只能一直向右走，所以每个格子路径数量为1
for (int j = 0; j < n; j++) {
dp[0][j] = 1;
}
// 填充整个dp表，从第二行和第二列开始，因为第一行和第一列已经初始化
for (int i = 1; i < m; i++) {
for (int j = 1; j < n; j++) {
dp[i][j] = dp[i - 1][j] + dp[i][j - 1]; // 路径数量等于上方和左方的路径数量之和
}
}
return dp[m - 1][n - 1]; // 返回到达右下角的路径数量
}
}
代码详解
-
初始化二维数组
dp：dp的大小为m x n，用于保存从起点(0, 0)到每个格子(i, j)的不同路径数量。
-
初始化边界条件：
dp[i][0] = 1：表示机器人在第一列的任意位置(i, 0)，由于只能向下移动到达这些位置，所以路径数量为1。dp[0][j] = 1：表示机器人在第一行的任意位置(0, j)，由于只能向右移动到达这些位置，所以路径数量为1。
-
状态转移计算：
- 从位置
(1, 1)开始，逐个计算每个位置的路径数量。对于任意位置(i, j)：- 机器人可以从上方
(i-1, j)或左方(i, j-1)移动到达(i, j)。 - 所以
dp[i][j]= 来自上方的路径数量dp[i-1][j]+ 来自左方的路径数量dp[i][j-1]。
- 机器人可以从上方
- 从位置
-
输出结果：
- 最终
dp[m-1][n-1]保存的是从左上角(0, 0)到右下角(m-1, n-1)的所有不同路径的总数。
- 最终
时间复杂度和空间复杂度
- 时间复杂度：
O(m * n)。我们需要遍历整个二维数组一次，每个位置计算一次。 - 空间复杂度：
O(m * n)。使用了一个m x n大小的二维数组来存储中间状态。
示例输出
假设 m = 3，n = 7：
1 1 1 1 1 1 1
1 2 3 4 5 6 7
1 3 6 10 15 21 28
dp[2][6] = 28表示从(0, 0)到(2, 6)有28条不同路径。
进一步优化（降维）
可以通过空间优化来降低空间复杂度。在计算当前行的路径数量时，只需要上一行的信息。因此，可以只用一维数组来保存当前行的路径数量，从而将空间复杂度从 O(m * n) 降低到 O(n)：
1 1 1 1 1 1 1
1 2 3 4 5 6 7
1 3 6 10 15 21 28
观察上述内容，不难发现，对初始行全1，他的后面两行对应自己上方的值（曾经的自己），加上自己左边的值（列数减去一），最左边的始终是1，对应dp【0】，因此，只需要有自己的数据，就可以更新自己在下一行的数据，有在下一行的数据，就可以向右边延伸，扩充整个数组，实际上还是二维，但是通过这种方式，缩减了空间占用
1 1+1 2+1 3+1 4+1 5+1—
1 2+1 3+3 4+6----
public int uniquePaths(int m, int n) {
int[] dp = new int[n];
Arrays.fill(dp, 1); // 初始化第一行
for (int i = 1; i < m; i++) {
for (int j = 1; j < n; j++) {
dp[j] += dp[j - 1]; // dp[j] = dp[j] + dp[j-1]
}
}
return dp[n - 1];
}
通过这种方式，利用 dp[j] 表示当前位置的路径数量，从而只用一维数组完成整个动态规划计算。
背包问题
0-1 背包问题
public class KnapsackProblem {
/*
1. n个物品都是固体，有重量和价值
2. 现在你要取走不超过 10克 的物品
3. 每次可以不拿或全拿，问最高价值是多少
编号 重量(g) 价值(元) 简称
1 4 1600 黄金一块 400 A
2 8 2400 红宝石一粒 300 R
3 5 30 白银一块 S
0 1 1_000_000 钻石一粒 D
1_001_630
1_002_400
*/
/*
1 2 3 4 5 6 7 8 9 10
a
a r
a r
d da da dr dr
*/
static class Item {
int index;
String name;
int weight;
int value;
public Item(int index, String name, int weight, int value) {
this.index = index;
this.name = name;
this.weight = weight;
this.value = value;
}
@Override
public String toString() {
return "Item(" + name + ")";
}
}
public static void main(String[] args) {
Item[] items = new Item[]{
new Item(1, "黄金", 4, 1600),
new Item(2, "宝石", 8, 2400),
new Item(3, "白银", 5, 30),
new Item(4, "钻石", 1, 10_000),
};
System.out.println(select(items, 10));
}
static int select(Item[] items, int total) {
int[][] dp = new int[items.length][total + 1];
print(dp);
Item item0 = items[0];
for (int j = 0; j < total + 1; j++) {
if (j >= item0.weight) {
dp[0][j] = item0.value;
}
}
print(dp);
for (int i = 1; i < dp.length; i++) {
Item item = items[i];
for (int j = 1; j < total + 1; j++) {
// x: 上一次同容量背包的最大价值
int x = dp[i - 1][j];
if (j >= item.weight) {
// j-item.weight: 当前背包容量-这次物品重量=剩余背包空间
// y: 剩余背包空间能装下的最大价值 + 这次物品价值
int y = dp[i - 1][j - item.weight] + item.value;
dp[i][j] = Integer.max(x, y);
} else {
dp[i][j] = x;
}
}
print(dp);
}
return dp[dp.length - 1][total];
}
static void print(int[][] dp) {
System.out.println(" " + "-".repeat(63));
Object[] array = IntStream.range(0, dp[0].length + 1).boxed().toArray();
System.out.printf(("%5d ".repeat(dp[0].length)) + "%n", array);
for (int[] d : dp) {
array = Arrays.stream(d).boxed().toArray();
System.out.printf(("%5d ".repeat(d.length)) + "%n", array);
}
}
}
降维
static int select(Item[] items, int total) {
int[] dp = new int[total + 1];
for (Item item : items) {
for (int j = total; j > 0; j--) {
if (j >= item.weight) { // 装得下
dp[j] = Integer.max(dp[j], item.value + dp[j - item.weight]);
}
}
System.out.println(Arrays.toString(dp));
}
return dp[total];
}
注意：内层循环需要倒序，否则 dp[j - item.weight] 的结果会被提前覆盖
分析
0-1 背包问题概述
0-1 背包问题是一个经典的动态规划问题。在这个问题中，你有一个背包，其最大容量为 total（单位为重量），以及若干个物品，每个物品有一个重量 weight 和一个价值 value。你需要决定如何选择物品，使得放入背包的物品总重量不超过背包的最大容量，同时总价值最大。
在 0-1 背包问题中，每个物品只能选择一次（即每个物品要么放入背包，要么不放入背包），这就是问题名称中的 “0-1” 的含义。
问题描述与代码解析
给定一些物品和背包的最大容量，总目标是找到一种选取物品的方式，使得选取的物品总重量不超过给定的容量，同时其总价值最大。
代码中有两种解法：
- 二维数组解法：使用二维动态规划表
dp[i][j]来保存前i个物品在容量j的情况下所能得到的最大价值，第一行代表只加入第一个物品，第二行代表两个物品，最后四行，代表总物品种类数，对应了所有物品，列代表的是整体的最大容量限制。在换入新行的时候，容量不够，就依据上一行补数据，容量足够，就进行价值比对，替换更优的数据，做到当行最优，下一行只需要和上一行比对即可。总结对应：装不装得下，装的下，能不能优化价格，做出地推狮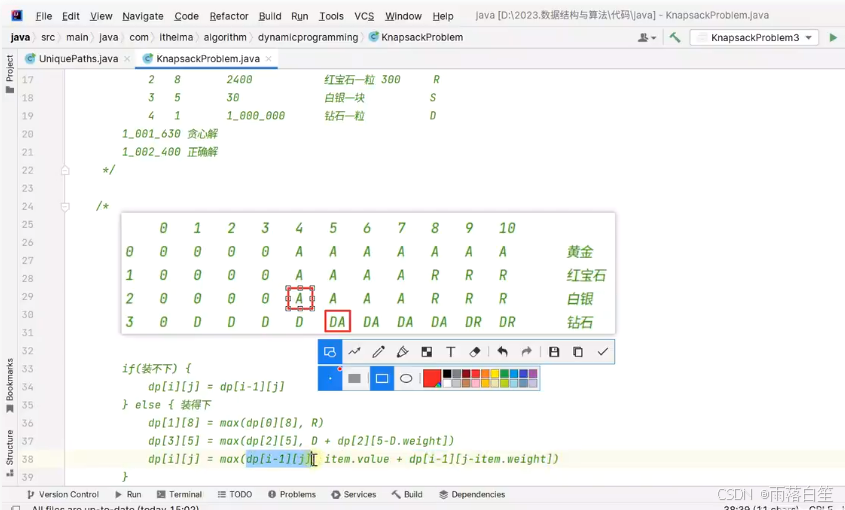
2. 一维数组解法（降维优化）：使用一维数组 dp[j]来保存容量为j的情况下所能得到的最大价值。
解法 1：二维数组解法
static int select(Item[] items, int total) {
int[][] dp = new int[items.length][total + 1]; // 创建一个二维数组用于动态规划
//行数是物品数，列数是0开始，到总数，0-1是负一，所以要特殊处理第一行数据
// 初始化第一个物品的价值
Item item0 = items[0];
for (int j = 0; j < total + 1; j++) {
if (j >= item0.weight) {
dp[0][j] = item0.value;
}
}
// 遍历所有物品，从第2个物品开始
for (int i = 1; i < dp.length; i++) {
Item item = items[i];
for (int j = 1; j < total + 1; j++) {
// 取不放当前物品 i 时的最大价值
int x = dp[i - 1][j];//如果是黄金，i=0，减1就负数了
if (j >= item.weight) {
// y 表示当前物品 i 放入背包后的最大价值：放入后的价值加上剩下空间的最大价值
int y = dp[i - 1][j - item.weight] + item.value;
dp[i][j] = Integer.max(x, y); // 取两者的最大值
} else {
dp[i][j] = x; // 当前物品 i 的重量大于背包容量，不能放入
}
}
}
return dp[dp.length - 1][total]; // 返回最后一个状态值，即最大价值
}
代码解析
-
二维数组
dp的含义：dp[i][j]表示在前i个物品中，容量为j的背包所能装入的最大价值。 -
初始化第一个物品：对于第一个物品，如果背包容量
j大于等于第一个物品的重量item0.weight，那么可以装入背包，dp[0][j]等于第一个物品的价值item0.value。 -
动态规划状态转移：
x表示不放当前物品i时的最大价值（即前i-1个物品的最大价值）。y表示放当前物品i后的最大价值，等于背包容量减去当前物品的重量后的最大价值，加上当前物品的价值。dp[i][j] = Math.max(x, y)，表示对于当前容量j，在前i个物品中可以选择的最大价值。
-
最终结果：
dp[dp.length - 1][total]保存了在所有物品和给定容量total下的最大价值。
解法 2：一维数组解法（降维优化）
在这个解法中，我们使用一维数组来优化空间复杂度。
static int select(Item[] items, int total) {
int[] dp = new int[total + 1]; // 创建一个一维数组用于动态规划
// 遍历每个物品
for (Item item : items) {
// 从后往前遍历背包容量，避免覆盖上一次的计算结果
for (int j = total; j > 0; j--) {
if (j >= item.weight) { // 当前容量能装得下当前物品
dp[j] = Integer.max(dp[j], item.value + dp[j - item.weight]); // 取两者最大值
}
}
System.out.println(Arrays.toString(dp)); // 打印当前状态
}
return dp[total]; // 返回最大价值
}
代码解析
-
一维数组
dp的含义：dp[j]表示容量为j的背包所能装入的最大价值。 -
倒序遍历容量：
- 从后往前遍历
j是为了防止在更新dp[j]时覆盖掉前面已经计算过的值。 - 每次只考虑一个物品，更新背包从容量
total到item.weight的所有可能状态。
- 从后往前遍历
-
状态转移：
- 如果
j >= item.weight，则当前背包容量可以装下当前物品。 dp[j]更新为两个情况的最大值：- 不放当前物品的最大价值：
dp[j] - 放当前物品的最大价值：
item.value + dp[j - item.weight]（当前物品的价值加上剩余容量的最大价值）
- 不放当前物品的最大价值：
- 如果
-
空间优化：
- 通过一维数组
dp，将空间复杂度从O(n * W)降低到O(W)，其中W是背包的容量。
- 通过一维数组
完全背包问题
public class KnapsackProblemComplete {
static class Item {
int index;
String name;
int weight;
int value;
public Item(int index, String name, int weight, int value) {
this.index = index;
this.name = name;
this.weight = weight;
this.value = value;
}
@Override
public String toString() {
return "Item(" + name + ")";
}
}
public static void main(String[] args) {
Item[] items = new Item[]{
new Item(1, "青铜", 2, 3), // c
new Item(2, "白银", 3, 4), // s
new Item(3, "黄金", 4, 7), // a
};
System.out.println(select(items, 6));
}
/*
0 1 2 3 4 5 6
1 0 0 c c cc cc ccc
2 0 0 c s cc cs ccc
3 0 0 c s a a ac
*/
private static int select(Item[] items, int total) {
int[][] dp = new int[items.length][total + 1];
Item item0 = items[0];
for (int j = 0; j < total + 1; j++) {
if (j >= item0.weight) {
dp[0][j] = dp[0][j - item0.weight] + item0.value;
}
}
print(dp);
for (int i = 1; i < items.length; i++) {
Item item = items[i];
for (int j = 1; j < total + 1; j++) {
// x: 上一次同容量背包的最大价值
int x = dp[i - 1][j];
if (j >= item.weight) {
// j-item.weight: 当前背包容量-这次物品重量=剩余背包空间
// y: 剩余背包空间能装下的最大价值 + 这次物品价值
int y = dp[i][j - item.weight] + item.value;
dp[i][j] = Integer.max(x, y);
} else {
dp[i][j] = x;
}
}
print(dp);
}
return dp[dp.length - 1][total];
}
static void print(int[][] dp) {
System.out.println(" " + "-".repeat(63));
Object[] array = IntStream.range(0, dp[0].length + 1).boxed().toArray();
System.out.printf(("%5d ".repeat(dp[0].length)) + "%n", array);
for (int[] d : dp) {
array = Arrays.stream(d).boxed().toArray();
System.out.printf(("%5d ".repeat(d.length)) + "%n", array);
}
}
}
降维
private static int select(Item[] items, int total) {
int[] dp = new int[total + 1];
for (Item item : items) {
for (int j = 0; j < total + 1; j++) {
if (j >= item.weight) {
dp[j] = Integer.max(dp[j], dp[j - item.weight] + item.value);
}
}
System.out.println(Arrays.toString(dp));
}
return dp[total];
}
扫一扫
2万+
被折叠的 条评论
为什么被折叠?
到【灌水乐园】发言
