算法练习——二分 朋友分派

我的生日要到了！根据习俗，我需要将一些派分给大家。我有N个不同口味、不同大小的派。有F个朋友会来参加我的派对，每个人会拿到一块派（必须一个派的一块，不能由几个派的小块拼成；可以是一整个派）。

我的朋友们都特别小气，如果有人拿到更大的一块，就会开始抱怨。因此所有人拿到的派是同样大小的（但不需要是同样形状的），虽然这样有些派会被浪费，但总比搞砸整个派对好。当然，我也要给自己留一块，而这一块也要和其他人的同样大小。

请问我们每个人拿到的派最大是多少？每个派都是一个高为1，半径不等的圆柱体。

输入格式:

第一行包含两个正整数N和F，1 ≤ N, F ≤ 10 000，表示派的数量和朋友的数量。
第二行包含N个1到10000之间的整数，表示每个派的半径。

输出格式:

输出每个人能得到的最大的派的体积，精确到小数点后三位。

输入样例: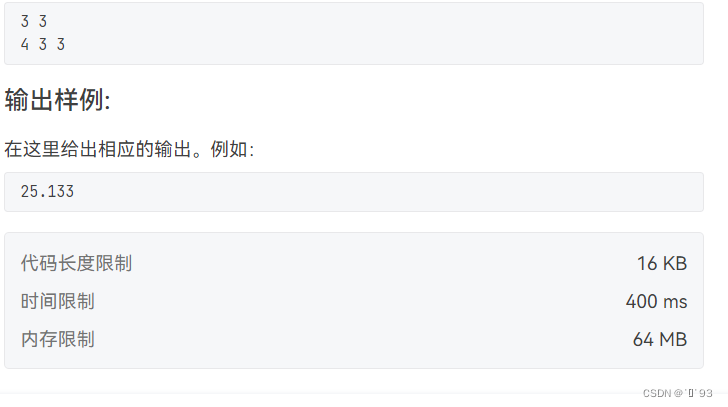

#include<iostream>
using namespace std;
#include<iomanip>
#include<algorithm> 
#define PI 3.1415926

int main()
{
	int n,x;
	double v[10000];
	cin>>n>>x;
	int r;
	for(int i = 0; i<n ; i++){
		cin>>r;
		v[i] = r*r*PI;
	};//读入数据 
	sort(v,v+n);
	double l = 0;
	double h = v[n-1];
	double mid;
	while((h-l)>1e-7){//趋近于零 
		int sum = 0;//计数器 
		mid = (l+h)/2;//中间值 
		for(int i = 0; i<n; i++){
			sum += (v[i]/mid);
		}
		if(sum == x+1) break;//x为要求的朋友数 
		else if( sum > x+1) l = mid;//多了人数，说明分的派体积过小 
		else h = mid; //反之分的派体积过大 
	}
	cout<<fixed<<setprecision(3)<<mid<<endl; //按要求输出 
	 return 0;
}