第十二章：目标识别_目标识别模型-优快云博客

决策理论方法识别是以使用决策(或判别)函数为基础的。令x= $(x_1,x_2,...,x_n)^T$ 表示一个n维模式向量。对于W个模式类 $w_1,w_2,...,w_w$ 决策理论模式识别的基本问题是依据下属性来找到W个决策函数 $d_1(x),d_2(x),...,d_w(x);$ 如果模式x属于类 $w_i$ ，则

$d_i(x)>d_j(x)\begin{matrix} & j=1,2,...,W;j\neq i \end{matrix}$

将x带入所有决策函数后，如果 $d_i$ (x)得到最大值，则称位置模式x属于第i个模式类。

从 $w_j$ 中分离出类 $w_i$ 的决策边界，由满足 $d_i(x)=d_j(x)$ 的x值给出，对于模式类 $w_i$ 有 $d_{ij}(x)>0$ ,而对于模式类 $w_j$ 有 $d_{ij}(x)<0$

2.1匹配

基于匹配的识别技术通过一个原型模式向量来表示每个类。

最小距离分类器

定义：根据一种预先定义的度量，将一个未知模式赋予最接近的类。

最小距离分类器由每个类的均值向量来确定：

$m_j=1/N\sum_{x\in w_j}^{}x_j\begin{matrix} & j=1,2,...,W \end{matrix}$

最小距离等同于计算函数：

对于一个最小的距离分类器，类 $w_i$ 和 $w_j$ 之间的决策边界为：

$\begin{matrix} d_{ij}(x)=d_i(x)-d_j(x)\\ =x^T(m_i-m_j)-1/2(m_i-m_j)^T(m_i+m_j)=0 \end{matrix}$

决策面是连接 $m_i$ 和 $m_j$ 的线段的垂直等分线

相关匹配

空间相关通过相关定理与函数的变换相联系：

归一化相关系数：

通常我们将w称为模板，将相关称为模板匹配。
通过移动该模板的中心(即增大x和y)，以便w的中心访问f中的每个像素，可得到所有的相关系数y(x, y)。寻找y(x, y )中的最大值，从而找到最好匹配的位置。如果y(x, y)中有多个位置出现最大值，表明w和f之间有多个匹配。

2.2最佳统计分类器

在平均意义上有可能推导出一种最佳分类方法，用该方法会产生最低的错误分类的概率。

基础知识

令分类器导致的损失记为Lij。

则平均损失为：

$r_j(x)=\sum_{k=1}^{W}L_{kj}p(w_k/x)$

通常称为"条件平均风险或损失"。

可以将该式简化为：

$r_j(x)=\sum_{k=1}^{W}L_{kj}p(x/w_k)P(w_k)$

高斯模式的贝叶斯分类器

将总体平均损失降至最低的分类器称为贝叶斯分类器。

由每个类的均值向量和协方差矩阵决定

贝叶斯决策函数：

在n维情形下，第j个模式类的向量的高斯密度为：

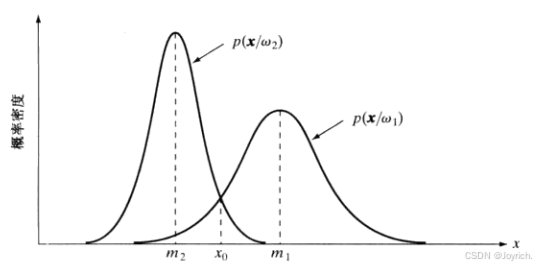
2.3神经网络

训练模式：用于估计参数（已知其所属的类）的模式

训练集：来自每个类的一组模式

学习或训练：使用训练集得到决策函数的过程

两个模式的感知机

在这种最基本的形式中，感知机学习一个线性决策函数，该决策函数对分两个线性可分的训练集。显示了两个模式类的感知机模型。这个基本装置的响应基于其输入的加权和，即

$d(x)=\sum_{i=1}^{n}w_ix_i+w_{n+1}$

这是一个与模式向量的分量有关的线性决策函数。称为权重的系数w,i = 1, 2,…, n,n+1在对输入求和前，对这些输人进行修正，并馈送到阈值单元中。在这一意义上，权重类似于人类神经系统中的神经突触。将求和连接的输出映射为该装置的最终输出的函数，有时称为激活函数。

当d(x)>0时，阈值单元使感知机的输出为+1，这表明模式r被识别为属于类o,。当d(x)<0时，情形正好相反。这种操作模式与之前的注释为两个类使用单个决策函数是一致的。当d(x)=0时,x位于分隔两个模式类的决策面上，这给出了一个不能确定的条件。由感知机实现的决策边界是通过d(x)等于零得到的:

图2.3中阈值单元的输出取决于d(x)的符号。替代测试整个函数来确定它是正还是负，我们可以对w.，此时系统的输出是

训练算法

线性可分的类：用于求两个线性可分训练集的权重向量解的一种简单迭代算法如下。

$w(k+1)=w(k)cy(k)$

该算法仅当正被考虑的模式在训练序列第k步被错误分类时，才改变w。假设修正增量c为正，现在它是一个常量。该算法有时称为固定增量校正准则。

当两个类的整个训练集循环通过机器而不出现任何错误时，该算法收敛。如果模式的两个训练集是线性可分的，那么固定增量校正准则会在有限步内收敛。称为感知机训练定理的该结果的证明，

不可分的类： 实际上，线性可分的模式类是个例外，通常情况并非如此。随着神经网络训练方面取得进展,解决不可分行为的许多方法已成为仅具有历史意义的课题。然而，一种早期的方法与该讨论直接相关,这就是原始的delta规则。称为感知机训练的Widrow-Hoff或最小均方(LMS)delta规则，该规则在任何训练步骤都使得在实际响应与期望响应间的误差最小。

考虑准则函数：

多层前馈神经网络

基本结构：它由多层结构上相同的计算节点(神经元)排列而成，从而一层中的每个神经元的输出送到下一层的每个神经元的输入。称为层 A 的第--层中的神经元的个数为N。通常，N。= n，它是输入模式向量的维度。称为0层的输出层中的神经元的数量表示为 $N_Q$ 。 $N_Q$ 等于w，即神经网络经训练后用于识别模式类的数量。如下面的讨论所示，如果该网络的第i个输出为“高”，而其他输出为“低”，则网络将模式向量x识别为属于类 $w_i$