LeetCode|二叉树|116.填充每个节点的下一个右侧节点指针 、117. 填充每个节点的下一个右侧节点指针 II 、 104.二叉树的最大深度 、111. 二叉树的最小深度

已于 2023-09-22 17:03:18 修改
阅读量242 收藏
点赞数
分类专栏： LeetCode 文章标签： leetcode 算法 c++ 数据结构
于 2023-09-22 17:03:04 首次发布
版权声明：本文为博主原创文章，遵循 CC 4.0 BY-SA 版权协议，转载请附上原文出处链接和本声明。
本文链接：https://blog.youkuaiyun.com/qq_62908989/article/details/133172119
版权

目录

一、116.填充每个节点的下一个右侧节点指针

1.题目描述

2.解题思路

3.代码实现

二、117. 填充每个节点的下一个右侧节点指针 II

1.题目描述

2.解题思路

3.代码实现

三、 104.二叉树的最大深度

1.题目描述

2.解题思路

3.代码实现（深度优先搜索）--递归

4.代码实现（广度优先搜索）--层序遍历

四、111. 二叉树的最小深度

1.题目描述

2.解题思路

3.代码实现(递归思想)

4.代码实现（层序遍历）

 

一、116.填充每个节点的下一个右侧节点指针

1.题目描述

给定一个 完美二叉树 ，其所有叶子节点都在同一层，每个父节点都有两个子节点。二叉树定义如下：

struct Node {
  int val;
  Node *left;
  Node *right;
  Node *next;
}

填充它的每个 next 指针，让这个指针指向其下一个右侧节点。如果找不到下一个右侧节点，则将 next 指针设置为 NULL。

初始状态下，所有 next 指针都被设置为 NULL。

示例 1：

输入：root = [1,2,3,4,5,6,7]
输出：[1,#,2,3,#,4,5,6,7,#]
解释：给定二叉树如图 A 所示，你的函数应该填充它的每个 next 指针，以指向其下一个右侧节点，如图 B 所示。序列化的输出按层序遍历排列，同一层节点由 next 指针连接，'#' 标志着每一层的结束。

示例 2:

输入：root = []
输出：[]

2.解题思路

        层序遍历，每层的最后一个节点next指向NULL，其余节点的next指向下一个节点。

3.代码实现

/*
// Definition for a Node.
class Node {
public:
    int val;
    Node* left;
    Node* right;
    Node* next;

    Node() : val(0), left(NULL), right(NULL), next(NULL) {}

    Node(int _val) : val(_val), left(NULL), right(NULL), next(NULL) {}

    Node(int _val, Node* _left, Node* _right, Node* _next)
        : val(_val), left(_left), right(_right), next(_next) {}
};
*/

class Solution {
public:
    Node* connect(Node* root) {
        queue<Node*> que;
        if(root == NULL) return NULL;
        que.push(root);
        while(!que.empty()){
            int size = que.size();//记录当前层的有多少个节点
            for(int i = 0;i < size;i++){
                //遍历当层每个节点
                Node* node = que.front();
                que.pop();
                //加入这个节点的左右孩子节点。
                if(node->left != NULL)  que.push(node->left);
                if(node->right != NULL) que.push(node->right);
                //添加左右孩子之后，如果是当前层的最后一个元素，则指向NULL；否则指向下一个节点
                if(i == size - 1){
                    node->next = NULL;
                }
                else{
                    node->next = que.front();
                }
            }
        }
        return root;
        
    }
};

二、117. 填充每个节点的下一个右侧节点指针 II

1.题目描述

给定一个二叉树：

struct Node {
  int val;
  Node *left;
  Node *right;
  Node *next;
}

填充它的每个 next 指针，让这个指针指向其下一个右侧节点。如果找不到下一个右侧节点，则将 next 指针设置为 NULL 。

初始状态下，所有 next 指针都被设置为 NULL 。

示例 1：

输入：root = [1,2,3,4,5,null,7]
输出：[1,#,2,3,#,4,5,7,#]
解释：给定二叉树如图 A 所示，你的函数应该填充它的每个 next 指针，以指向其下一个右侧节点，如图 B 所示。序列化输出按层序遍历顺序（由 next 指针连接），'#' 表示每层的末尾。

示例 2：

输入：root = []
输出：[]

2.解题思路

        和116那题一模一样，一个是完美二叉树，一个是二叉树。没什么本质差别。

3.代码实现

/*
// Definition for a Node.
class Node {
public:
    int val;
    Node* left;
    Node* right;
    Node* next;

    Node() : val(0), left(NULL), right(NULL), next(NULL) {}

    Node(int _val) : val(_val), left(NULL), right(NULL), next(NULL) {}

    Node(int _val, Node* _left, Node* _right, Node* _next)
        : val(_val), left(_left), right(_right), next(_next) {}
};
*/

class Solution {
public:
    Node* connect(Node* root) {
        queue<Node*> que;
        if(root == NULL) return NULL;
        que.push(root);
        while(!que.empty()){
            int size = que.size();
            for(int i = 0;i < size;i++){
                Node* node = que.front();
                que.pop();
                //添加左右孩子
                if(node->left != NULL) que.push(node->left);
                if(node->right != NULL) que.push(node->right);
                //如果是当层的最后一个节点，next就指向null；否则指向下一个节点
                if(i == size - 1)
                    node->next = NULL;
                else 
                    node->next = que.front();
            }
        }
        return root;
    }
};

三、 104.二叉树的最大深度

1.题目描述

给定一个二叉树 root ，返回其最大深度。

二叉树的 最大深度 是指从根节点到最远叶子节点的最长路径上的节点数。

示例 1：

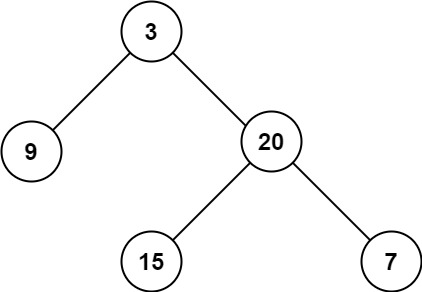
输入：root = [3,9,20,null,null,15,7]
输出：3

示例 2：

输入：root = [1,null,2]
输出：2

2.解题思路

  • 深度优先搜索：

        如果想知道整棵树的最大深度，就是要知道左子树l和右子树r的最大深度

        那么整棵树的最大深度就是max(l,r)+1

  • 广度优先搜索

        最大深度，就是计算多少层，层序遍历一下即可。 

3.代码实现（深度优先搜索）--递归

/**
 * Definition for a binary tree node.
 * struct TreeNode {
 *     int val;
 *     TreeNode *left;
 *     TreeNode *right;
 *     TreeNode() : val(0), left(nullptr), right(nullptr) {}
 *     TreeNode(int x) : val(x), left(nullptr), right(nullptr) {}
 *     TreeNode(int x, TreeNode *left, TreeNode *right) : val(x), left(left), right(right) {}
 * };
 */
class Solution {
public:
    int maxDepth(TreeNode* root) {
        //深度优先搜索
        //如果想知道整棵树的最大深度，就是要知道左子树l和右子树r的最大深度
        //那么整棵树的最大深度就是max(l,r)+1

        //开始写递归
        //触底反弹，遇到空指针了，说明该树为0
        if(root == NULL)    return 0;
        //超级操作，计算：左子树和右子树的最大深度 + 1
        return max(maxDepth(root->left),maxDepth(root->right)) + 1;
    }
};

4.代码实现（广度优先搜索）--层序遍历

/**
 * Definition for a binary tree node.
 * struct TreeNode {
 *     int val;
 *     TreeNode *left;
 *     TreeNode *right;
 *     TreeNode() : val(0), left(nullptr), right(nullptr) {}
 *     TreeNode(int x) : val(x), left(nullptr), right(nullptr) {}
 *     TreeNode(int x, TreeNode *left, TreeNode *right) : val(x), left(left), right(right) {}
 * };
 */
class Solution {
public:
    int maxDepth(TreeNode* root) {
        queue<TreeNode*> que;
        if(root == 0)   return 0;
        que.push(root);
        int depth = 0;//记录层数(深度)
        while(!que.empty()){
            int size = que.size();
            for(int i = 0;i < size;i++){
                TreeNode* node = que.front();
                que.pop();
                if(node->left != NULL)  que.push(node->left);
                if(node->right != NULL)  que.push(node->right);
            }
            depth++;
        }
        return depth;
    }
};

四、111. 二叉树的最小深度

1.题目描述

给定一个二叉树，找出其最小深度。

最小深度是从根节点到最近叶子节点的最短路径上的节点数量。

说明：叶子节点是指没有子节点的节点。

示例 1：

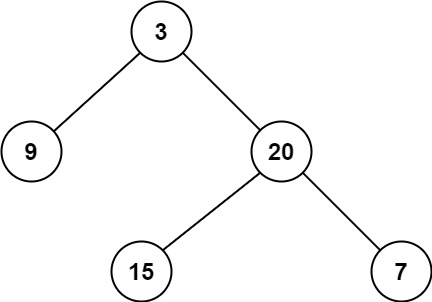
输入：root = [3,9,20,null,null,15,7]
输出：2

示例 2：

输入：root = [2,null,3,null,4,null,5,null,6]
输出：5

2.解题思路

  • 递归思想

本题关键就是找到叶子节点。 叶子节点的定义：左右孩子都为NULL时，就是叶子节点。

①如果root为NULL,直接return  0 就行；

②如果root左右孩子都不存在，return 1即可。

③如果当前节点  左右孩子都存在，说明root不是叶子节点并且也不知道叶子节点在哪一个孩子那边。所以此时    返回 左右孩子的最小深度 + 1

④如果当前节点  左右孩子有一个存在，说明当前节点的子节点中存叶子节点，所以此时 返回不为空的孩子节点的最小深度 + 1。

  • 层序遍历

遇到叶子节点，也就是左右孩子都为NULL，则返回这个节点所在层数 。

3.代码实现(递归思想)

/**
 * Definition for a binary tree node.
 * struct TreeNode {
 *     int val;
 *     TreeNode *left;
 *     TreeNode *right;
 *     TreeNode() : val(0), left(nullptr), right(nullptr) {}
 *     TreeNode(int x) : val(x), left(nullptr), right(nullptr) {}
 *     TreeNode(int x, TreeNode *left, TreeNode *right) : val(x), left(left), right(right) {}
 * };
 */
class Solution {
public:
    int minDepth(TreeNode* root) {
        //递归思想
        //这里需要注意出口条件，也就是找到那个叶子节点
        if(root == NULL)    return 0;
        //分三种情况
        //1.如果左右孩子都是空，说明达到了叶子结点，返回1
        if(root->left == NULL && root->right == NULL)  return 1;
        //2.如果左右孩子都存在，说明当前节点不是叶子节点，返回较小的孩子节点深度
        if(root->left && root->right)
            return 1 + min(minDepth(root->left),minDepth(root->right));
        //3.如果左右孩子有一个不存在，说明当前节点的子节点中存在叶子节点
        //因此返回不为空的孩子节点的最小深度
            return 1 + max(minDepth(root->left),minDepth(root->right));
    }
};

4.代码实现（层序遍历）

/**
 * Definition for a binary tree node.
 * struct TreeNode {
 *     int val;
 *     TreeNode *left;
 *     TreeNode *right;
 *     TreeNode() : val(0), left(nullptr), right(nullptr) {}
 *     TreeNode(int x) : val(x), left(nullptr), right(nullptr) {}
 *     TreeNode(int x, TreeNode *left, TreeNode *right) : val(x), left(left), right(right) {}
 * };
 */
class Solution {
public:
    int minDepth(TreeNode* root) {
        //层序遍历
        //当左右孩子都为空，说明符合抵达叶子节点，返回当前层数就行
        queue<TreeNode*> que;
        if(root == NULL)    return 0;
        que.push(root);
        int depth = 0;
        while(!que.empty()){
            int size = que.size();
            for(int i = 0;i < size;i++){
                TreeNode* node = que.front();
                que.pop();
                //push两个孩子节点
                if(node->left != NULL)  que.push(node->left);
                if(node->right != NULL)  que.push(node->right);
                //如果两个孩子都为空，说明抵达叶子节点
                if(!node->left && !node->right)
                    return depth + 1;
            }
            depth++;
        }
        return depth;
    }
};

评论 1
添加红包

请填写红包祝福语或标题

个

红包个数最小为10个

元

红包金额最低5元

当前余额3.43元 前往充值 >
需支付：10.00元
成就一亿技术人!
领取后你会自动成为博主和红包主的粉丝 规则
hope_wisdom
发出的红包
实付元
使用余额支付
点击重新获取
扫码支付
钱包余额 0

抵扣说明：

1.余额是钱包充值的虚拟货币，按照1:1的比例进行支付金额的抵扣。
2.余额无法直接购买下载，可以购买VIP、付费专栏及课程。

余额充值