力扣每日一题day03-209.长度最小的子数组

给定一个含有 n 个正整数的数组和一个正整数 target 。

找出该数组中满足其总和大于等于 target 的长度最小的 连续子数组 [numsl, numsl+1, ..., numsr-1, numsr] ，并返回其长度。如果不存在符合条件的子数组，返回 0 。

示例 1：

输入：target = 7, nums = [2,3,1,2,4,3]
输出：2
解释：子数组 [4,3] 是该条件下的长度最小的子数组。
示例 2：
输入：target = 4, nums = [1,4,4]
输出：1

示例 3：
输入：target = 11, nums = [1,1,1,1,1,1,1,1]
输出：0

暴力解法：

暴力解法就市两个for循环，不断寻找符合条件的子序列

• 时间复杂度为O(n^2)

本题目暴力解法会超时

代码：

class Solution {
    public int minSubArrayLen(int target, int[] nums) {
        int result=Integer.MAX_VALUE;//最终结果
        int sum=0;//子序列的数值之和
        int subLength=0;//子序列长度
        for(int i=0;i<nums.length;i++){//设置子序列起点为i
            sum=0;
            for(int j=i;j<nums.length;j++){//设置子序列终点位置为j
                sum+=nums[j];
                if(sum>=target){//一旦子序列和大于等于target，更新result
                    subLength=j-i+1;//取子序列长度
                    result=result<subLength?result:subLength;
                    break;//一旦符合条件就break
                }
            }
        }
        return result==Integer.MAX_VALUE?0:result;//如果result没有赋值返回0
    }
}

滑动窗口：

滑动窗口就是不断调整子序列的起始位置和终止位置，从而得到我们想要的结果。

在暴力解法中一个for循环为窗口的起始位置，一个for循环为窗口的终止位置，用两个for循环完成一个不断搜索的过程。

滑动窗口用一个for循环完成。

首先要思考如果用一个for循环，那么应该表示起始位置还是终止位置？如果用一个for循环来表示起始位置，那么该如何遍历剩下的终止位置？所以这个循环的索引一定是滑动窗口的终止位置

本题中实现滑动窗口主要确定以下三点：

• 窗口内的元素是什么？

• 如何移动窗口的起始位置

• 如何移动窗口的终止位置

窗口内的元素：保持窗口内数值总和大于或等于s的最小的连续子数组

移动窗口的起始位置：如果当前窗口的值大于s，则窗口向前移动（即缩小窗口）

移动窗口的结束位置：窗口的结束位置就是for循环遍历数组的指针

如何移动起始位置？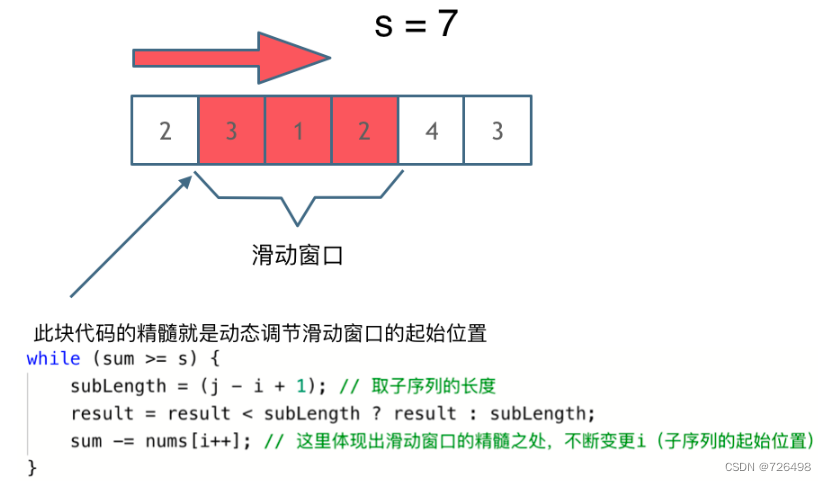

可以发现滑动窗口的精妙之处在于根据当前子序列和大小的情况，不断调节子序列的起始位置。从而将O(n^2)暴力解法降为O(n)。

代码：

class Solution {
    public int minSubArrayLen(int target, int[] nums) {
        int result=Integer.MAX_VALUE;
        int sum=0;//滑动窗口数值之和
        int i=0;//滑动窗口起始位置
        int subLength=0;//滑动窗口长度
        for(int j=0;j<nums.length;j++){
            sum+=nums[j];
            //每次更新起始位置，不断比较子序列是否符合条件
            while(sum>=target){
                subLength=j-i+1;//取子序列长度
                result=result<subLength?result:subLength;
                sum-=nums[i++];//不断变更起始位置 i
            }
        }
        return result==Integer.MAX_VALUE?0:result;
    }
}