double与float那点事

浮点数在计算机中的存储方式

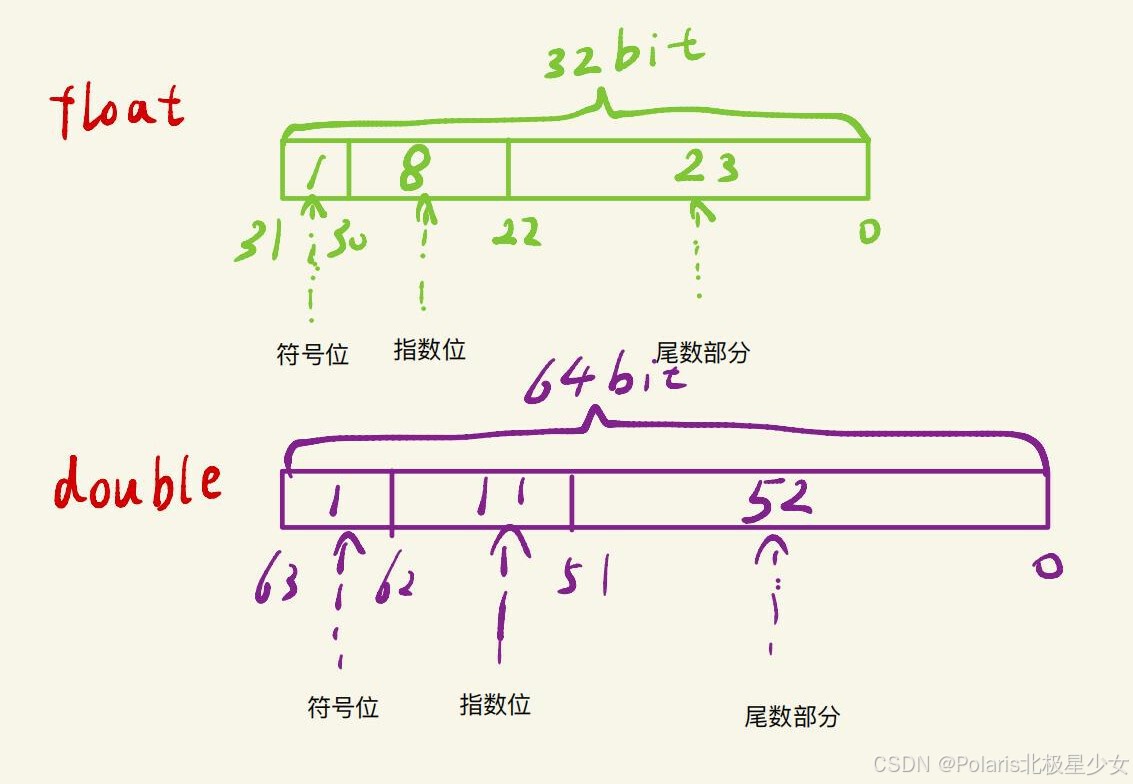
C语言中，对于浮点类型的数据采用单精度类型（float）和双精度类型(double)来存储，float数据占用32bit,double数据占用64bit,float和double在存储方式上都是遵从IEEE的规范的，float遵从的是IEEE R32.24 ,而double 遵从的是R64.53。

无论是单精度还是双精度在存储中都分为三个部分：

1. 符号位(Sign) : 0代表正，1代表为负
2. 指数位（Exponent）:用于存储科学计数法中的指数数据，并且采用移位存储
3. 尾数部分（Mantissa）：尾数部分

  R32.24和R64.53的存储方式都是用科学计数法来存储数据的，比如5.75用十进制的科学计数法表示就为:,而200.5可以表示为:,但在计算机存储中，首先要将上面的数更改为二进制的科学计数法表示，5.75用二进制表示可表示为101.11,200.5用二进制表示为：11001000.1用二进制的科学计数法表示101.11可以表示为，11001000.1可以表示为

二进制和十进制的转换机制

一、十进制转换成二进制

1.1 正整数转二进制

要点：除二取余，倒序排列，高位补零。

方法：将正的十进制数除以二，得到的商再除以二，依次类推直至商为0或1时为止，然后在旁边标出各步的余数，最后倒着写出来，高位补零。

注：计算机内部表示数的字节单位是定长的，如8位，16位，或32位。所以，位数不够时，高位补零。

1.2 负整数转二进制

方法：先将对应的正整数转换成二进制后，对二进制取反，然后对结果再加1。

1.3 小数转二进制

方法：对小数点以后的数×2，取结果的整数部分，然后再用小数部分再×2，再取结果的整数部分……以此类推，直到小数部分为0或者位数足够为止。然后把取的整数部分按先后次序排列，就构成了二进制小数部分的序列。

二、二进制转换成十进制

2.1 整数二进制转换为十进制

方法：首先将二进制数补齐位数，首位如果是0就代表是正整数，如果首位是1则代表是负整数。

若首位是0的正整数，补齐位数以后，将二进制中的位数分别与对应的值相乘，然后相加得到的就为十进制。

若二进制补足位数后首位为1时，就需要先取反再换算。

2.2 小数二进制转换为十进制

方法：将二进制中的位数分别与对应的值相乘，然后相加，得到的值即为换算后的十进制。

上述方法来源：二进制和十进制的转换机制是什么?_转化成二进制-腾讯云开发者社区-腾讯云方法：将正的十进制数除以二，得到的商再除以二，依次类推直至商为0或1时为止，然后在旁边标出各步的余数，最后倒着写出来，高位补零。https://cloud.tencent.com/developer/article/2149695

存储转换过程

任何一个数的科学计数法表示都为,尾数部分就可以表示为xxxx,可以将小数点前面的1省略，所以23bit的尾数部分，可以表示的精度却变成了24bit，道理就是在这里，那24bit能精确到小数点后几位呢，我们知道9的二进制表示为1001，所以4bit能精确十进制中的1位小数点，24bit就能使float能精确到小数点后6位，而对于指数部分，因为指数可正可负，8位的指数位能表示的指数范围就应该为:-127-128了

指数范围计算

• 指数位的 8 位可以表示的值范围是从 0 到 255。
• 在偏移量为 127 的情况下：
  • 最小指数值：0 - 127 = -127
  • 最大指数值：255 - 127 = 128

因此，8 位的指数位能表示的实际指数范围是从 −127到 128。

指数部分的存储采用移位存储，存储的数据为元数据+127，下面就看看5.75和200.5在内存中真正的存储方式。

首先看下5.75，用二进制的科学计数法表示为:

按照上面的存储方式，符号位为:0，表示为正，指数位为:2+127=129 ,故5.75的存储方式如下图所示:

而单精度浮点数200.5的存储方式如下图所示:

那么如果给出内存中一段数据，并且告诉你是单精度存储的话，你如何知道该数据的十进制数值呢？其实就是对上面的反推过程，比如给出如下内存数据：01000011010010001000000000000000，首先我们现将该数据分段，0 10000 0110 100 1000 1000 0000 0000 0000，在内存中的存储就为下图所示：

根据我们的计算方式，可以计算出，这样一组数据表示为:

而双精度浮点数的存储和单精度的存储大同小异，不同的是指数部分和尾数部分的位数。所以这里不再详细的介绍双精度的存储方式了，下方是200.5的最后存储方式图

存储转换计算文章来源：

浮点数在计算机中存储方式 - Robin Zhang - 博客园https://www.cnblogs.com/jillzhang/archive/2007/06/24/793901.html

浮点数的范围与精度

float的指数范围为-127~+128，而double的指数范围为-1023~+1024，并且指数位是按补码的形式来划分的。

其中负指数决定了浮点数所能表达的绝对值最小的非零数；

而正指数决定了浮点数所能表达的绝对值最大的数，也即决定了浮点数的取值范围。

float的范围为-2^128 ~ +2^128，也即-3.40E+38 ~ +3.40E+38；

double的范围为-2^1024 ~ +2^1024，也即-1.79E+308 ~ +1.79E+308。

float和double的精度是由尾数的位数来决定的。浮点数在内存中是按科学计数法来存储的，其整数部分始终是一个隐含着的“1”，由于它是不变的，故不能对精度造成影响。

float：2^23 = 8388608，一共七位，这意味着最多能有7位有效数字，但绝对能保证的为6位，也即float的精度为6~7位有效数字；

double：2^52 = 4503599627370496，一共16位，同理，double的精度为15~16位。

浮点数的有效数字精度是通过二进制有效位数和十进制位数之间的换算得到的。具体来说，精度是由二进制尾数（即有效数字位数）的位宽决定的。

1. 有效位数的转换公式
二进制的有效数字位数n与十进制的有效数字位数d的近似关系是：

其中。

2. 单精度浮点数（32 位）
单精度浮点数的有效数字为24 位二进制位（包括隐式位）。

使用公式计算：

因此，单精度浮点数的有效数字对应大约7 位十进制数字。

3. 双精度浮点数（64 位）
双精度浮点数的有效数字为53 位二进制位（包括隐式位）。

使用公式计算：

因此，双精度浮点数的有效数字对应大约15 到 16 位十进制数字。