本文详细解析了PyTorch中几个重要的张量操作和神经网络层，包括torch.randn生成随机张量，torch.nn.BatchNorm2d的标准化处理，nn.ConvTranspose2d的转置卷积，以及ReLU、Tanh、leaky_relu和sigmoid等激活函数的作用和特点。此外，还介绍了x.squeeze()的维度压缩功能和nn.linear的全连接层操作。
目录
（1）torch.rand解析
m=torch.randn(2,3)
tensor([[ 1.7612, -0.2392, 0.2091],
[ 0.0080, 2.5092, 0.1154]])m=torch.randn(3,2,3)
tensor([[[ 0.0281, 2.3753, -0.5443],
[ 0.2180, 1.6471, 0.2749]],
[[ 0.2063, 0.9097, -0.2529],
[-0.0416, -1.6361, 0.5904]],
[[-1.0617, -2.1073, 1.1950],
[-1.9227, -0.3732, -0.5089]]])m=torch.randn(2,3,2,3)
tensor([[[[-0.4535, -0.4844, 1.8255],
[-0.3293, -1.1086, 0.2057]],
[[-0.8840, -0.2336, -0.0681],
[ 0.0429, -0.0969, -0.3101]],
[[ 0.5239, -0.2162, 0.8850],
[-1.8782, 0.4279, 0.9713]]],
[[[ 2.2144, -1.5748, -0.4556],
[-1.0815, -1.8373, 0.7370]],
[[-1.2699, -0.2101, 1.1468],
[-0.3367, 0.1314, 1.0151]],
[[-0.5115, 0.0841, 0.8001],
[ 1.4264, -0.4094, 0.0511]]]])
torch.randn[batch, channel, height, width] ，分别表示图像批次，图像通道数，以及图像的高宽。
（2）torch.nn.BatchNorm2d解析
torch.nn.BatchNorm2d(num_features, eps=1e-05, momentum=0.1, affine=True, track_running_stats=True, device=None, dtype=None)
函数原理
num_features：输入图像的通道数量。
eps：稳定系数，防止分母出现0。
momentum：模型均值和方差更新时的参数，见上述公式。
affine：代表gamma，beta是否可学。如果设为True，代表两个参数是通过学习得到的；如果设为False，代表两个参数是固定值，默认情况下，gamma是1，beta是0。
track_running_stats：代表训练阶段是否更新模型存储的均值和方差，即测试阶段的均值与方差的计算方法采用第一种方法还是第二种方法。如果设为True，则代表训练阶段每次迭代都会更新模型存储的均值和方差(计算全局数据)，测试过程中利用存储的均值和方差对各个通道进行标准化处理；如果设为False，则模型不会存储均值和方差，训练过程中也不会更新均值和方差的数据，测试过程中只计算当前输入图像的均值和方差数据(局部数据)。具体区别见代码案例。
此函数是对四维数组进行标准化处理，对于所有的batch中的同一个channel的数据元素进行标准化处理，即如果有C个通道，无论有多少个batch，都会在通道维度上进行标准化处理，一共进行C次。（可以只赋一个值保证通道数一致即可运行）
注：训练阶段的均值和方差计算方法相同，将所有batch相同通道的值取出来，一块计算均值和方差，即计算当前观测值的均值和方差。
测试阶段的均值和方差有两种计算方法：
①估计所有图片的均值和方差，即做全局计算
②采用和训练阶段相同的计算方法，即只计算当前输入数据的均值和方差
x = torch.tensor([[[[1., 1.],
[2., 1.]],
[[1., 1.],
[-1., -1.]],
[[1., 1.],
[6., 6.]]]], )
n = torch.nn.BatchNorm2d(3)
print(n(x))out：
tensor([[[[-0.5773, -0.5773],
[ 1.7320, -0.5773]],
[[ 1.0000, 1.0000],
[-1.0000, -1.0000]],
[[-1.0000, -1.0000],
[ 1.0000, 1.0000]]]], grad_fn=<NativeBatchNormBackward0>)x = torch.tensor([[[[-0.7150, -0.3002],
[-0.0198, 1.4544]],
[[1, 1],
[2, 2]],
[[-0.2248, 1.4212],
[-1.1535, 0.5693]]],
[[[-1.2423, -0.7024],
[-0.2578, 1.7831]],
[[1, 1],
[2, 2]],
[[1.0156, -1.7779],
[0.2642, -0.1141]]]], )
n = torch.nn.BatchNorm2d(3)
print(n(x))out：
tensor([[[[-0.7150, -0.3002],
[-0.0198, 1.4544]],
[[-1.0000, -1.0000],
[ 1.0000, 1.0000]],
[[-0.2248, 1.4212],
[-1.1535, 0.5693]]],
[[[-1.2423, -0.7024],
[-0.2578, 1.7831]],
[[-1.0000, -1.0000],
[ 1.0000, 1.0000]],
[[ 1.0156, -1.7779],
[ 0.2642, -0.1141]]]], grad_fn=<NativeBatchNormBackward0>)
进程已结束,退出代码0
用途：
- 训练过程中遇到收敛速度很慢的问题时，可以通过引入BN层来加快网络模型的收敛速度
- 遇到梯度消失或者梯度爆炸的问题时，可以考虑引入BN层来解决
- 一般情况下，还可以通过引入BN层来加快网络的训练速度
（3）nn.ConvTranspose2d解析
nn.ConvTranspose2d(ngf * 8, ngf * 4, 4, 2, 1, bias=False)若ngf=128，则是将通道数由1024转化为512，图像变大2倍，使用了4*4的卷积核，stride=2, padding=1
下面展示由三通道转化为单通道图像，图像由2*2变成了4*4，图像大小取决于卷积核，步长，以及padding。与通道数无关。图像大小可看做与Conv相反。
x = torch.tensor([[[[1., 1.],
[2., 1.]],
[[1., 1.],
[-1., -1.]],
[[1., 1.],
[6., 6.]]]], )
n = torch.nn.ConvTranspose2d(3,1,4,2,1)
print(n(x))out:
tensor([[[[-0.3537, -0.4574, -0.2223, -0.4182],
[-1.3329, 1.5825, -2.8556, 1.0986],
[-0.2595, -0.7639, 0.5412, -1.2538],
[-1.5081, -0.5554, -1.9544, -0.3093]]]],
grad_fn=<ConvolutionBackward0>)in_channels和out_channels互换一下，其他参数都与Conv2d设置一致。经过转置卷积运算得到尺寸为输出特征图，达到了恢复分辨率的效果，减少了通道数，使得图像变大，结合DCGAN生成器模型图便可理解
此处看该博客详细讲解nn.ConvTranspose2d详解_CtrlZ1的博客-优快云博客_nn.convtranspose2d
（4）ReLU解析
激活函数作用：线性模型的表达能力不够，引入激活函数是为了添加非线性因素。在神经网络中，为了避免单纯的线性组合，我们在每一层的输出后面都添加一个激活函数（sigmoid、tanh、ReLu等等）
ReLU，全称为：Rectified Linear Unit，是一种生成器中用的激活函数，通常意义下，其指代数学中的斜坡函数，即f(x)=max(0,x)
而在神经网络中，ReLU函数作为神经元的激活函数，在卷积与批量标准化之后使用。
（5）Tahn解析
函数表达式
函数图像
解决了sigmoid函数收敛变慢的问题，相对于sigmoid提高了收敛速度。
（6）leaky_relu解析
函数表达式
函数图像
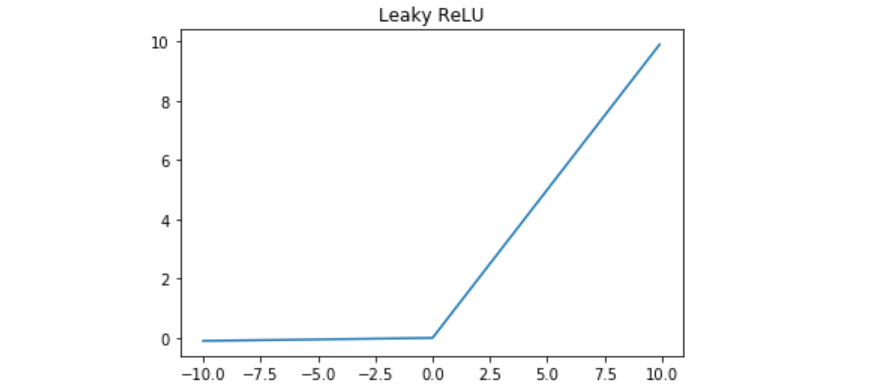
Leaky ReLU函数的特点：
- Leaky ReLU函数通过把x的非常小的线性分量给予负输入0.01来调整负值的零梯度问题。
- Leaky有助于扩大ReLU函数的范围，通常α 的值为0.01左右。
- Leaky ReLU的函数范围是负无穷到正无穷。
（7）sigmoid解析
Sigmoid函数常被用作神经网络的激活函数，将变量映射到[0,1]之间.函数解析式如下。
Sigmoid可以将任何值转换为0~1概率，用于二分类问题。
tan是sigmoid的变形
函数及其导数图像，蓝色原来的函数，橙色是导数
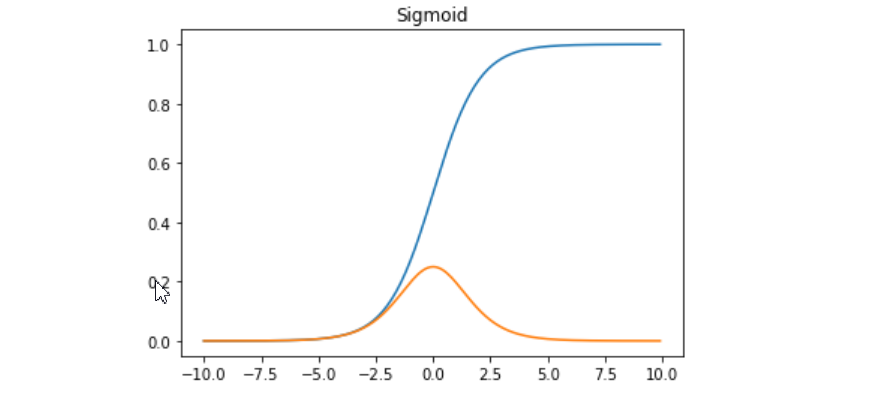
Sigmoid函数的特性与优缺点：
- Sigmoid函数的输出范围是0到1。由于输出值限定在0到1，因此它对每个神经元的输出进行了归一化。
- 用于将预测概率作为输出的模型。由于概率的取值范围是0到1，因此Sigmoid函数非常合适梯度平滑，避免跳跃的输出值
- 函数是可微的。这意味着可以找到任意两个点的Sigmoid曲线的斜率明确的预测，即非常接近1或0。
- 函数输出不是以0为中心的，这会降低权重更新的效率
- Sigmoid函数执行指数运算，计算机运行得较慢。
- Sigmoids saturate and kill gradients. 这就是我们常常提到的梯度消失问题啦。sigmoid 有一个非常致命的缺点，当输入非常大或者非常小的时候（saturation），这些神经元的梯度是接近于0的，从图中可以看出梯度的趋势。所以，你需要尤其注意参数的初始值来尽量避免saturation的情况。如果你的初始值很大的话，大部分神经元可能都会处在saturation的状态而把gradient kill掉，这会导致网络变的很难学习。
其他激活函数的了解可参照：机器学习中的数学——激活函数
（8）x.squeeze()解析
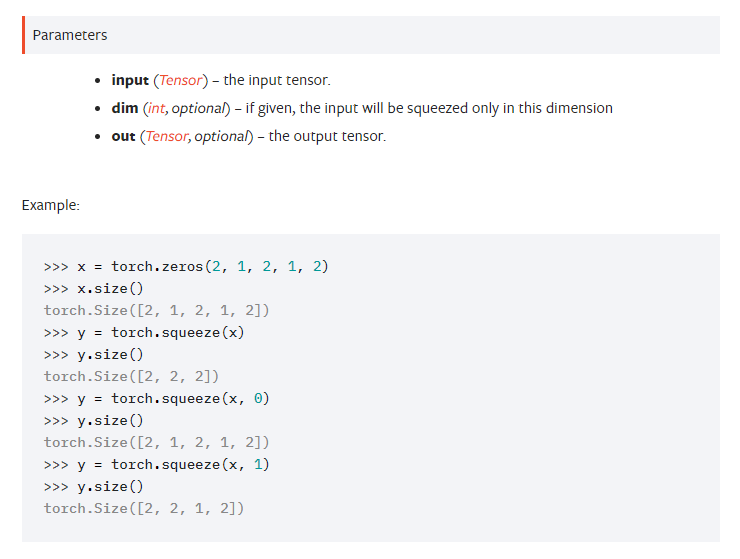
squeeze()函数的功能是维度压缩。返回一个tensor（张量），其中 input 中大小为1的所有维都已删除。当给定 dim 时，那么只在给定的维度（dimension）上进行压缩操作。官方解释如下:
（9）nn.linear(x)解析
in_features指的是输入的二维张量的大小，即输入的[batch_size, size]中的size。out_features指的是输出的二维张量的大小，即输出的二维张量的形状为[batch_size，output_size]中的output_size，当然，它也代表了该全连接层的神经元个数。
在神经网络分类问题中，一般有几个种类output_size就是几。对于DGGAN可以把最后的激活函数sigmoid换成linear，输出为1。
m = torch.randn(2, 3, 2, 2)
m=m.view(2, -1)
liner = torch.nn.Linear(12, 1)
out = liner(m)
print(out.shape)out：
torch.Size([2, 1])（10）x.normal_与x.fill_解析
torch.normal_返回一个张量，包含从给定参数means,std的离散正态分布中抽取随机数.
- means (Tensor) – 均值
- std (Tensor) – 标准差
- out (Tensor) – 可选的输出张量
a=torch.ones([2,3])
print(a)
b=a.normal_(0,0.1)
print(b)
out:
tensor([[1., 1., 1.],
[1., 1., 1.]])
tensor([[-0.0812, -0.0544, -0.1440],
[-0.0367, 0.0721, -0.1393]])x.fill_(a)就是将矩阵全部填入a。
扫一扫
3960
被折叠的 条评论
为什么被折叠?
到【灌水乐园】发言
