第1节 多层神经网络

第1节 多层神经网络

在上一节课，学习了一个神经元的结构，如图所示，输入x，它有一个权重w，偏置b加在预测值$\hat{y}$上，它表示一个线性的函数$\hat{y}$=wx+b，画出来是一条直线，因此它成为线性的模型linear model。

局限性/缺点：无法实现一些复杂任务，如把正方形和三角形分开、拟合分段函数。

那么一个神经元不行，我们思考多个神经元组合连接在一起行不行？

更复杂的神经网络

此时我们输入的不再是一个x，而是多个x（多个输入）；联想到数学知识，二元函数、多元函数，有多个自变量的函数，这个神经网络也如此。b相当于常数，可以合并。这个看似复杂的模型，其实里面全都是这种线性的关系。

人类大脑神经与神经元

人类大脑：接收到信息，做出相应的反应/出现相应的想法。

AI：接收到信息，也能做出相应的反应，所以神经元一开始就是模仿人类大脑设计的。

手上有很多条神经末梢–>ai有多个神经元传输信息

神经元与矩阵

线性方程组：

这样，一个复杂的神经网络，就可以写成矩阵运算的形式：

和y = b + wx的形式一模一样。

输出的r₁r₂r₃作为下一个运算的输入，权重是c₁c₂c₃，进行同样的运算，得到预测值$\hat{y}$

$\hat{y}$ = c₁r₁+c₂r₂+c₃r₃+b = b + (c₁,c₂,c₃)(r₁r₂r₃)^T

一般我们写向量竖着写，所以可以写成$\hat{y}$ = b+c^Tr

神经元的串联

刚才的公式只是把神经元简单地串联了起来，似乎只有传递的作用，通过突触全等地传递给下一个神经元，那么一根和多根没有区别，即单纯的加深网络没有任何意义。下面在数学上验证：

把前两个式子代入第三个式子得：

把x₁的系数提出来作为α₁，把x₂的系数提出来作为α₂。最后得到的形式，和只有一层的r的表达式形式是一样的。参数是可以改变、可以学习的，对于参数来说只要学习到一个合适的值就可以了，关键在于输入的形式，神经网络加深后的表达式（输入的式子）都一样了，仍然是一个单层的神经网络，加深就没有意义了。

---

但是人类的神经元并不是简单、全等传递的，神经元自己是有一点决定权的。

生物神经元具有兴奋和抑制两种状态，当接受的刺激高于一定阈值时，则会进入兴奋状态并将神经冲动由轴突传出，反之则没有神经冲动。第一次闻到榴莲的人，就会感到臭，是因为接受的刺激高于了阈值；经常在榴莲环境下的人，就感觉不到臭了，因为阈值提高了，原本的刺激达不到现在的阈值了。

人类的神经末梢感受的信息，如温度、湿度、压力，就可以传递给大脑，但这个传递不是完全线性的传递，可能这个伤口不是特别疼，你就会忽略它。在神经网络中，这个处理刺激的功能就是激活函数，使收到的刺激不是全等的传递，而要做一定的筛选。

激活函数的位置位于中间输出r的后面，输出r后就给他上一个激活函数。

输入x1x2x3，权值w11 w21 w31得到了r1

输入x1x2x3，权值w12 w22 w32得到了r2

输入x1x2x3，权值w13 w23 w33得到了r3

激活r1，r1本身的刺激较小，就不传递它；激活r2，r2本身的刺激高于阈值，传递；激活r3，r3本身的刺激高于阈值，传递。总之，激活函数可以对输出做一个筛选，超过这个阈值的我们留下，低于这个阈值的我们不要。

激活函数和非线性元素

如果没有激活函数，无论网络多么复杂，最后的输出都是输入的线性组合。而纯粹的线性组合并不能解决复杂的问题。

引入激活函数后，由于激活函数都是非线性的，这样就给神经元引入了非线性元素，使得神经网络可以逼近任何非线性函数，这使得神经网络能够应用到更多非线性模型中。

sigmoid：假如x很小，输出0，x是0，输出0.5，x很大，输出1。

relu：假如x小于0，就输出0，都不要了；x比零大，就输出x。

想画一个圆就可以用激活函数，横坐标小纵坐标大它就可以往上拐弯，无数个神经元只能画直线，但加上激活函数就能拐出一个圆，这就叫引入了非线性元素。

激活函数最重要的特性：能求导！

原因：当我们得到模型的输出、也就是预测值后，要和真实值去比较，需要用到损失函数Loss，Loss要对参数求偏导得到梯度，参数通过减去学习率乘梯度来更新参数，不断使loss减小，达到理想的模型。由于神经网络的层次深，要更新前面的参数需要用到链式求导，如果中间有一步无法求导，那么就无法得到梯度的结果，也就没法更新参数，没法优化模型。

另外，注意到relu函数0的地方不能求导，但是我们用的32位浮点数，一般取不到0这个位置，所以忽略。即使打到0了，目前也已有很多解决方法。

激活函数位置

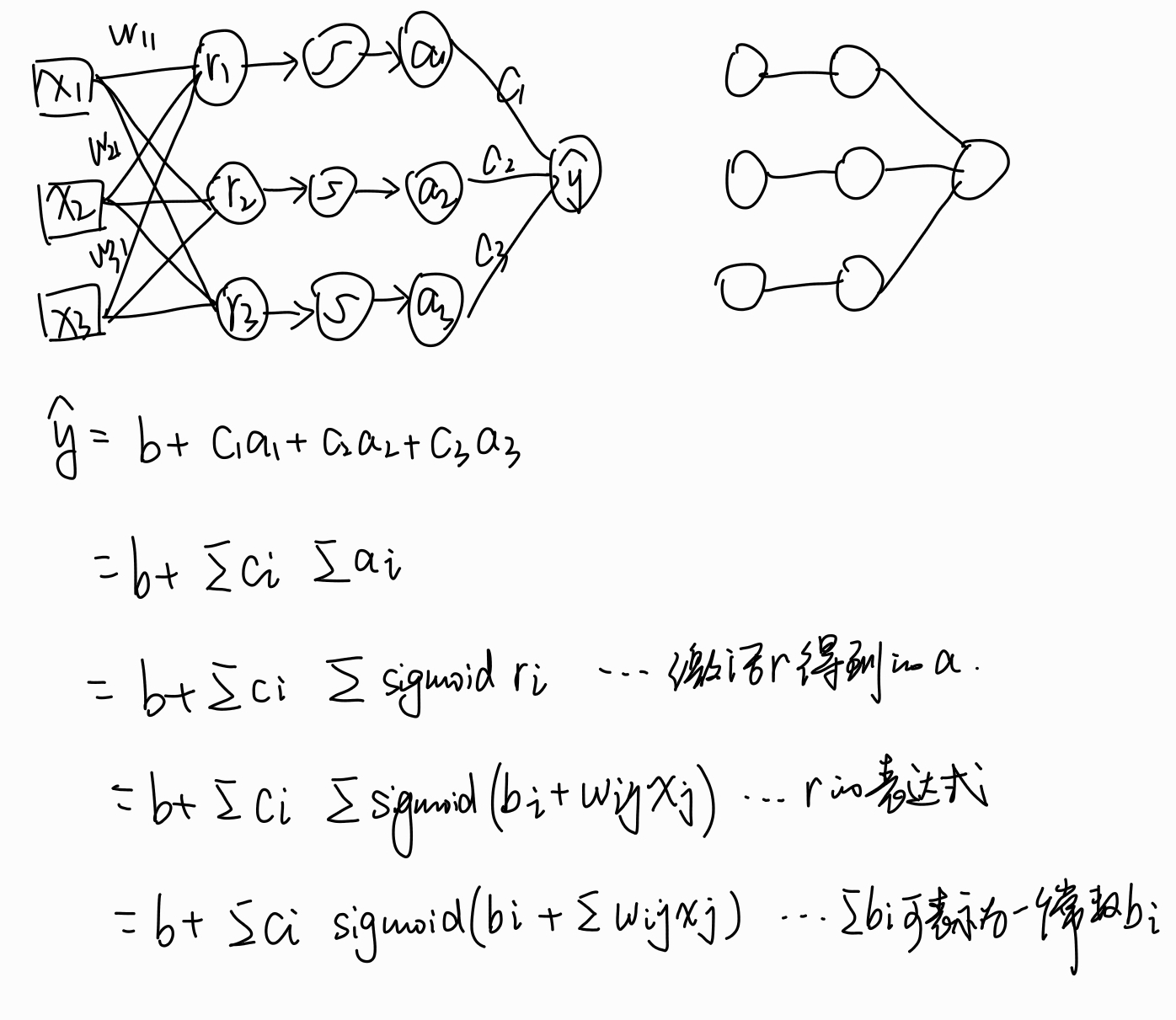
用σ表示激活函数，r出去后让他经过一个激活函数，再进入下一个线性组合。

a=σ(r) 加粗说明是向量

激活函数预测实例

用relu拟合分段函数：激活r1得到了一个relu蓝线，激活r2得到了下面的那个relu蓝线，分别赋予不同的权值，最后可以组合出来一个分段函数红线。上面说的只是一种可能的情况，实际的神经网络是个黑匣子，我们也不知道激活哪个出来的是上面的relu蓝线，也不知道激活哪个出来的是下面的relu蓝线，总之最后能够拐弯、拟合出红线。如果没有激活函数让它拐弯，无论如何都组合不出分段函数的。

模型整体结构

简图

详图

矩阵运算

上面三个表示的是同一个东西。

为什么可以说神经网络是一个矩阵运算？因为一个神经网络是由多个线性运算的神经元组成的，这些数学线性运算写在一起就是一个线性方程组，而线性方程组能够写成矩阵运算的形式，因此神经网络本身就是个矩阵运算。

神经网络的参数

x是特征输入feature，y尖是预测输出，剩下的都是需要训练的参数unknown parameters

把这些矩阵拉直，写成竖着的向量的形式

我们用θ来表示这些未知的参数，能够把这些所有的参数统一一下，这样我们写损失函数L的时候，就不必写成L(w11,w12,…b11,b12,…,c1…)，写成L(θ)就行。

深度学习的训练过程

大的模型如何进行训练呢？和训练一个神经元的步骤一样。

Step1 定义一个函数

Step2 定义一个合适的损失函数

L要对参数进行求导，上节课只有一个参数，求一次偏导即可，但是现在有很多参数，L要对所有参数进行求导，但是L是关于$\hat{y}$的函数，假如最后那个权值是w₁₀，那L得先对y尖求导，y尖再对w10求导，才能得到L对w10的导数；那要求第一个权值w1，L得先对y尖求导，y尖再对w10求导，w10再对w9求导，再对w8求导，再对w7求导，再对w6求导，再对w5求导，再对w4求导，再对w3求导，再对w2求导，再对w1求导，得到L对w1的导数，这样一个链式求导法则。

这个往回求出每一个参数的导数的过程叫做梯度回传过程。

往前求y尖的过程叫做前向过程。

这个更新参数的方法叫做Gradient Descent梯度下降。

导数是某个点的方向，梯度是某个点下降最快的方向。

既然朝着下降最快的方向走，那就是想让我们的loss变小。

Step3 根据损失对模型进行优化

复杂loss

如果是绝对值的那个loss，我们很容易看出loss的最低点。但一个复杂网络，loss也会很复杂，我们就没办法求出来loss的解析式，不知道往哪走才是最低点。最开始我们只有一个“瞎猜的”参数，只有一个点，我们只能通过梯度回传一点点去试，没法一下子就知道哪里是最低点。

loss还可能是个三维平面，无论loss是什么样，我们都严格梯度回传、求导的步骤来训练参数。

loss的面在非欧氏空间内。欧氏空间：近就是近远就是远。非欧氏空间：两点必须通过曲面才能到达，看似近的两点，实际距离远。更没法人为去揣测loss是什么样，但只要给神经网络一个loss，它就可以按照公式去进行更新参数。

来起个名字吧

每两层之间的每一个点都相连，叫做全连接神经网络Fully Connected Network（FC）

连接的边叫做weight权重，加给神经元的b叫做bias偏差，中间的每个圈叫做神经元Neuron，连成的网络叫做神经网络Neural Network。上个世纪五十年代已经出现神经网络了，但是当时的显卡很差，没法承担起这么大的网络，导致运算的结果很差，论文的审稿人看到Neural Network，发现它的效果很差，后来再看到这个名字他们就不看了，之后显卡没有明显发展，于是就被搁置掉了，现在显卡发展起来了，效果变好了，发论文如果还叫以前的名字，担心审稿人就不想看了，于是就改了名字叫Deep Learning。

Deep = Many hidden layers 许多隐藏层

2012年AlexNet后开始做深度学习，它的错误率是16.4%。

2015年的Residual Net错误率是3.57%，有152layers

它使用了一个特殊的结构：Residual connect残差连接，解决了随着网络深度增加而出现的梯度消失或梯度爆炸问题。

输出后，再把输入引入到输出层。

代码演示

1. 上一层的输出数，和这一层的输入要匹配；这一层的输出，和下一层的输入要匹配

2. 去掉relu对非线性函数的表示：没有激活函数，只能拟合直线，有了激活函数，很快就能拟合曲线。

3. 浅深层对函数的表示能力：层数太浅太深都会影响拟合效果，

   太浅会欠拟合，没有办法表示；太深会过拟合，模型很骄傲，把每个点当作真实数据，都放在自己的函数上，会导致梯度太大没法表示，出现梯度爆炸。

4. 界外预测：训练集在-5到5，测试集在-5到10，发现-5到5能够成功拟合，5-10表现很差直接跑飞了。模型对于没有见过的，预测能力会差一些。