关于浮点数在计算机内存中的存储

开篇我们先写下一个公式，

任意浮点数可以用二进制表示为 (-1)^S * M * 2^E

S代表数的正负，当数为正时，S=0；当数为负时，S=1；

M表示有效数字，大于等于1，小于2。

E表示指数位。

S

我们举个例子 9.0，

显然9.0是正数，所以其S=0；

M

之后我们把9.0转换为一个暂时的二进制数字，即1001.0；

这时我们用科学计数法表示一下1001.0，可以表示为1.0010 * 2^3；

（因为1001.0是二进制数，所以底数为2，1.0010 * 2^3；因为小数点向左移动了三位，所以指数为3，1.0010 * 2^3；）

那么根据开篇提到的公式：

任意浮点数可以用二进制表示为 (-1)^S * M * 2^E；

那么 9.0 = (-1)^0 * 1.0010 * 2^3；

所以我们是不是只要把 S M E 三个数字存储起来，就可以表示一个浮点数了？

当然可以！

对于32位的浮点数，即float类型，我们按 S E M 的顺序存储分别占用1 8 23个比特位；

对于64位，即double类型，S E M 分别占 1 11 52 个比特位；

这时我们再补充一些细节，前面提到M的值是大于等于1，小于2的，也就是M一定是1.xxxxx，

那么为了节省空间，前面的 1 我们去掉，直接把xxxxx当成M，未来再拿出来使用这个数时，我们再给它加上 1 。也就是 9.0 在计算机中存储的 M 值是0010，不是10010哦。

E

（E的情况十分复杂，这里只讲一部分，若我后面有时间，会专门再研究一下 E）

（为了方便，以下数据均为float类型，double类型与之类似）

根据国际标准，E是一个无符号整型，也就是说，占8位的E所表示的范围是 0~255 。这其实是很奇怪的，因为科学计数法是可以出现指数为负数的。举个例子：

我们将0.5用二进制表示一下，为0.1

（这里简单讲解一下，在二进制中，小数点前第一位权重为2^0，再往前一位为2^1……以此类推，小数点后第一位权重为2^(-1)，再往后一位为2^(-2)……所以二进制的0.1转换为十进制就是0 * 2^0 . 1 * 2^(-1) = 0.5）

根据刚刚讲过的，M大于等于1小于2，所以将0.1化为 1.0 * 2^(-1);

这时就变成了 S=0，M=1.0，E=-1； 

但是E是无符号整型，怎么存 -1呢？

根据国际标准，我们存入E的真实值时必须加上一个中间数，对于float，这个中间数为127.

这时E=-1+127=126；

实践是检验真理的唯一标准

光学不练，等于没练，我们上机试验一下：

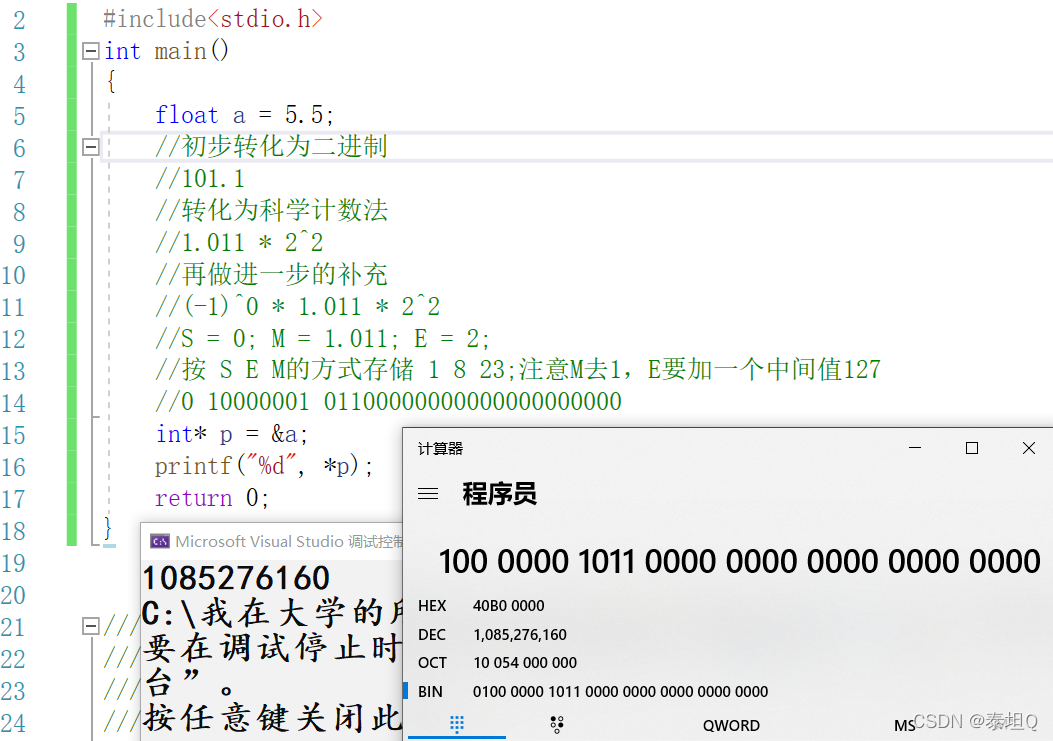
我们看到，以整型的形式打印浮点数5.5，结果与我们推测的一致。

至此，关于我个人对浮点数在计算机中的存储也就结束了，如果后面有时间或者再学习中遇到了更复杂的情况，我会再更详细记录一下E的各种情况并作分析。