C语言递归求汉诺塔的移动次数

汉诺塔规则：有三根柱子其中一个柱子上按从小到大的顺序摆放着N个圆盘，把圆盘按大小顺序重新摆放在另一根柱子上。并且规定，在小圆盘上不能放大圆盘，在三根柱子之间一次只能移动一个圆盘。

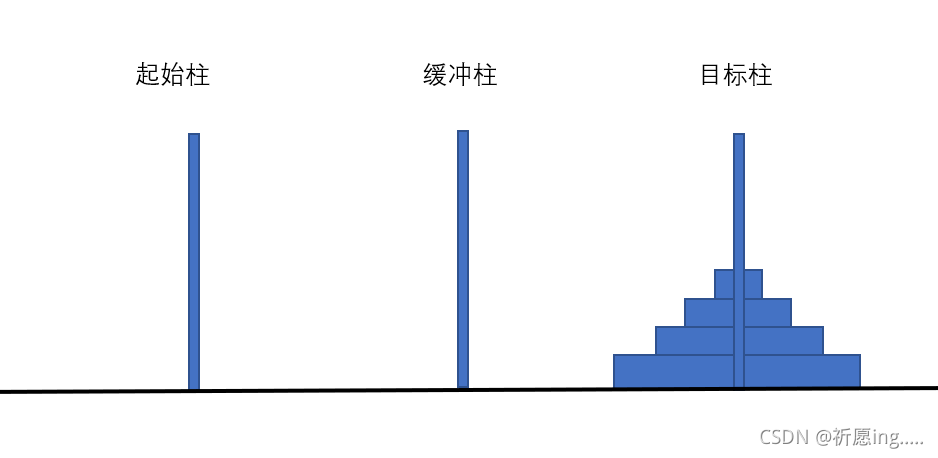
如图为四层汉诺塔

 以上图 4层汉诺塔为例

 为方便区分为柱子命名，现在是要将起始柱上的圆盘移动到目标柱上。

        首先我们将过程分为三个部分

第一部分：为了将最底层的圆盘移动到目标柱，我们既要保持最底层圆盘上无其他圆盘又要保证目标柱上无圆盘，于是再规则的限制下我们必须将其转化为如下形态，所需移动次数记为n1。

第二部分：将底层圆盘移动到目标柱，如图，所需移动次数为 1

 第三部分：将缓冲柱上的圆盘悉数移动到目标柱上，如图，所需移动次数记为n2

 在三个部分中第二步次数固定为1，而仔细观察便可发现，由于在一，三部分中最大圆盘不移动且不影响其它圆盘，所以一，三部分都是在进行一个三层的汉诺塔问题（故n1=n2），只不过是以缓冲柱为目标柱，在此我们便发现了递归。

我们记n层汉诺塔问题的移动次数为Hanoi(n)。

而在上述例子中我们将四层汉诺塔问题转化为了两次三层汉诺塔问题加一

即    Hanoi(4) = 2*Hanoi(3)+1;

同理Hanoi(3) = 2*Hanoi(3)+1;

       Hanoi(2) = 2*Hanoi(1)+1;

而Hanoi(1)即为将一个圆盘移动到目标柱上所需移动次数为1

则n层汉诺塔的递归为

        Hanoi(n) = 2*Hanoi(n-1)+1;

代码为

#include<stdio.h>

int Hanoi(int n)//创建汉诺塔问题的函数 
{
	if(n>=2)
	return 2*Hanoi(n-1)+1;//此处即为函数的递归，返回n层汉诺塔所需移动次数
	else
	return 1;//返回一层汉诺塔所需次数 
}


int main(){
	int a;
	printf("请输入汉诺塔层数"); 
	scanf("%d",&a); 
	int b = Hanoi(a);//引用函数 
	printf("共需要移动 %d 次",b);
	return 0;
}

ps：由于整型的限制该代码仅可计算较小层数的汉诺塔问题