离散数学·代数结构【二元关系及其性质、代数系统】

练习放在文末

n元运算的定义

实例

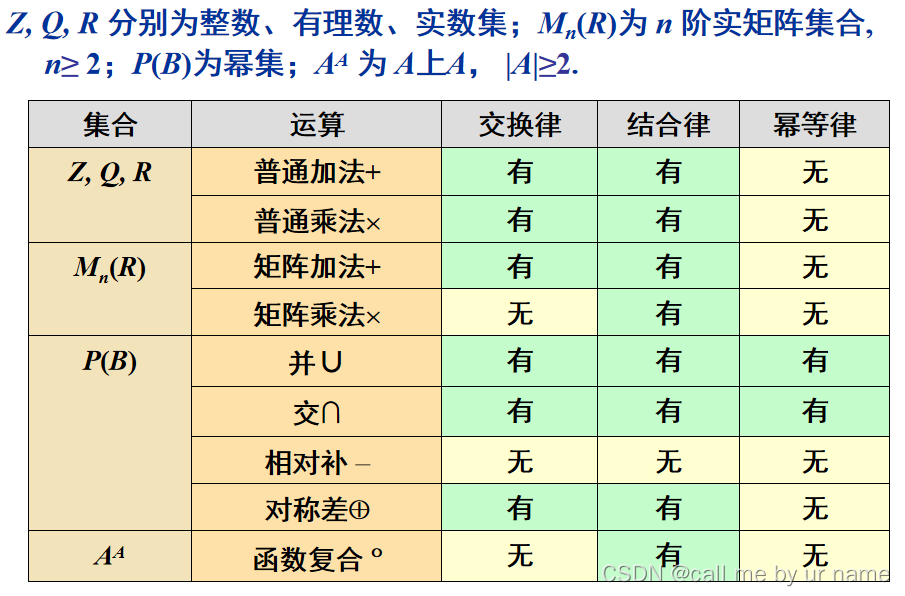
算律

 

其中，这2个⚪和*只是代指某一个运算符（并不是真的有这2个运算符）

实例

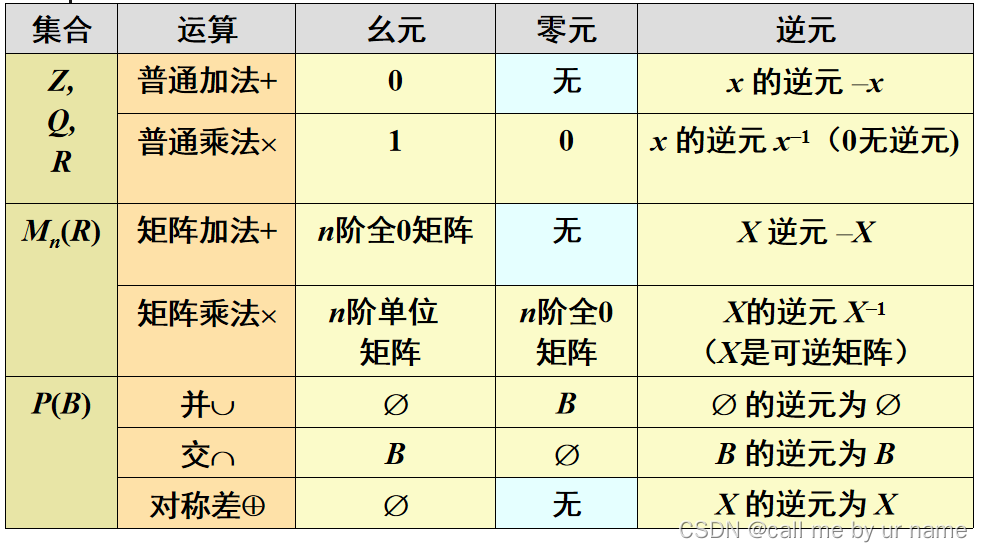
特异元素

性质

实例

消去律定义

例题

由运算表判别算律的方法

 

 例题

代数系统的定义

记法一用得比较少

实例

分类

这个构成成分比较抽象，不是指载体，是指载体的性质。运算个数——如果是无穷集，那么就是一样的

子代数

这个例子之所以不是，是因为没有满足零元运算（单位元不同）

封闭是指运算完之后的结果仍在载体中

最大、最小、平凡子代数

最小子代数就是所有代数常数组成的集合，并且封闭

例子

首先，nz和Z的构成成分相同，是同类型的。接着，+满足的（+特殊的性质）单位元，拿到nz上运算，满足，即可知满足

n=0只有一个0，所以是真子代数

n=1就是Z本身

n>1既不是本身，也不是最小子代数

积代数

积代数的载体是两个因子代数的载体相乘

运算集这里比较抽象，难以直接解释。但是积代数的元素（各个有序对）中，前一项是V1的运算（用V1有序对的前一项和V2有序对的前一项运算），后一项是V2的运算（这里同理）。这样解释比较清晰

题目

题目用来辅助

15题

步骤：

1.做卡氏积

2.得到卡氏积后，用有序对和所有有序对（包括自己）做积代数的运算（本题中——<1,5>和<2,6>作积代数运算——<1【V1运算符】2，5【V2运算符】6>——<2,5>） 

性质

简而言之——因子代数满足，在积代数中对应就满足什么（不满足消去律，消去律这个一直比较特殊）

练习

1题

这题主要是看看运算表

4题（1）~（5）

第一个——减法不满足任何算律，并且减法是没有单位元的（可以看看单位元的定义，要满足交换的形式，即e a=a e，明显减法不存在单位元）

第二个——因为未包含 0 ，所以，没有零元

7题

是否构成代数系统——看运算是否封闭