【CF】Day23——Codeforces Round 766 BD + Codeforces Round 980 CD + Codeforces Round 951 C

于 2025-04-03 11:56:58 发布
阅读量714 收藏 19
点赞数 30
文章标签： 算法
版权声明：本文为博主原创文章，遵循 CC 4.0 BY-SA 版权协议，转载请附上原文出处链接和本声明。
本文链接：https://blog.youkuaiyun.com/qq_61422664/article/details/146976912
版权

B. Not Sitting

题目：

思路：

似曾相识的题（社恐社牛选座位

题目的意思很简单，就是我们可以先让几个位置不让 A 选，然后再让A选，A选完后B可以随便坐，现在问他们两个的距离

我们先看简单情况，假设只有一行，那么显然我们只需要让 B 坐 1 或 n 的位置即可，因为 A 的最佳位置就是中间，所以我们坐两边即可，同理，如果只有一列我们也只需要坐两端

注意到题目的距离是 x 的差 + y 的差，也就是说二者是独立的，因此 B 的最佳选择肯定是坐四个角落，那 A 的位置呢？显然由于每次都是选择最佳的位置，所以我们可以枚举所有的位置到四个角落的距离，然后取最大值，那么我们排完序后按顺序输出即可

为什么呢？因为我们涂位置的最佳方式就是从距离最小的点开始涂，那么就是每次都会把一个 A 的最佳位置涂了，所以 A 每次都要往后选

代码：

#include <iostream>
#include <algorithm>
#include<cstring>
#include<cctype>
#include<string>
#include <set>
#include <vector>
#include <cmath>
#include <queue>
#include <unordered_set>
#include <map>
#include <unordered_map>
#include <stack>
#include <memory>
using namespace std;
#define int long long
#define yes cout << "YES\n"
#define no cout << "NO\n"

void solve()
{
    int n, m;
    cin >> n >> m;
    multiset<int> ans;
    for (int i = 0; i < n; i++)
    {
        for (int j = 0; j < m; j++)
        {
            int mx = max(i, n - i - 1) + max(j, m - j - 1);
            ans.insert(mx);
        }
    }
    for (auto x : ans)
    {
        cout << x << " ";
    }
    cout << endl;
}

signed main()
{
    cin.tie(0)->sync_with_stdio(false);
    int t = 1;
    cin >> t;
    while (t--)
    {
        solve();
    }
    return 0;
}

D. Not Adding

题目：

思路：

数学题，思维

首先我们要知道一个结论就是 gcd(a,b,c) = gcd(gcd(a,b),c)

也就是说我们的gcd其实是固定的，那么我们就要考虑每一步的操作能不能造成奉献

观察到题目的数据很小，只有1e6，那我们可要尝试考虑打表

对于任意一个数 x，我们去看看数组中是否存在 x 的倍数，如果有 x 的倍数，那么最后只要选这几个倍数就可能能凑出 x，为什么是可能呢？因为有可能这几个倍数被gcd不一定是 x，可能是 kx，所以我们最后枚举完还要检查一下最后的 gcd 是不是 x，同时原数组中不能有 x 

代码：

#include <iostream>
#include <algorithm>
#include<cstring>
#include<cctype>
#include<string>
#include <set>
#include <vector>
#include <cmath>
#include <queue>
#include <unordered_set>
#include <map>
#include <unordered_map>
#include <stack>
#include <memory>
using namespace std;
#define int long long
#define yes cout << "YES\n"
#define no cout << "NO\n"

int gcd(int a, int b)
{
    return !b ? a : gcd(b, a % b);
}


void solve()
{
    int n;
    cin >> n;
    vector<int> a(n);
    vector<int> has(1e6 + 1, 0);
    for (int i = 0; i < n; i++)
    {
        cin >> a[i];
        has[a[i]] = 1;
    }
    int ans = 0;
    for (int i = 1; i <= 1e6; i++)
    {
        int p = 0;
        for (int j = i; j <= 1e6; j+=i)
        {
            if (has[j])
                p = gcd(p, j);
        }
        if (p == i && !has[p])
            ans++;
    }
    cout << ans;
}

signed main()
{
    cin.tie(0)->sync_with_stdio(false);
    int t = 1;
    //cin >> t;
    while (t--)
    {
        solve();
    }
    return 0;
}

C. Concatenation of Arrays

题目：

思路：

没啥意思的题

对于这题就是分类讨论，我们假设有两个 [a,b] [c,d]，然后草稿纸分别枚举他们的大小关系和最后的结果，最后发现总和大的放后面是在每种情况中都是最优的，所以按这样排就行了

猜猜题 

代码：

#include <iostream>
#include <algorithm>
#include<cstring>
#include<cctype>
#include<string>
#include <set>
#include <vector>
#include <cmath>
#include <queue>
#include <unordered_set>
#include <map>
#include <unordered_map>
#include <stack>
#include <memory>
using namespace std;
#define int long long
#define yes cout << "YES\n"
#define no cout << "NO\n"

void solve()
{
    int n;
    cin >> n;
    vector<pair<int, int>> p(n);
    for (int i = 0; i < n; i++)
    {
        cin >> p[i].first >> p[i].second;
    }
    sort(p.begin(), p.end(), [](pair<int, int> a, pair<int, int> b) {
        return (a.first + a.second) < (b.first + b.second); });
    for (auto x : p)
    {
        cout << x.first << " " << x.second << " ";
    }
    cout << endl;
}

signed main()
{
    cin.tie(0)->sync_with_stdio(false);
    int t = 1;
    cin >> t;
    while (t--)
    {
        solve();
    }
    return 0;
}

D. Skipping

题目：

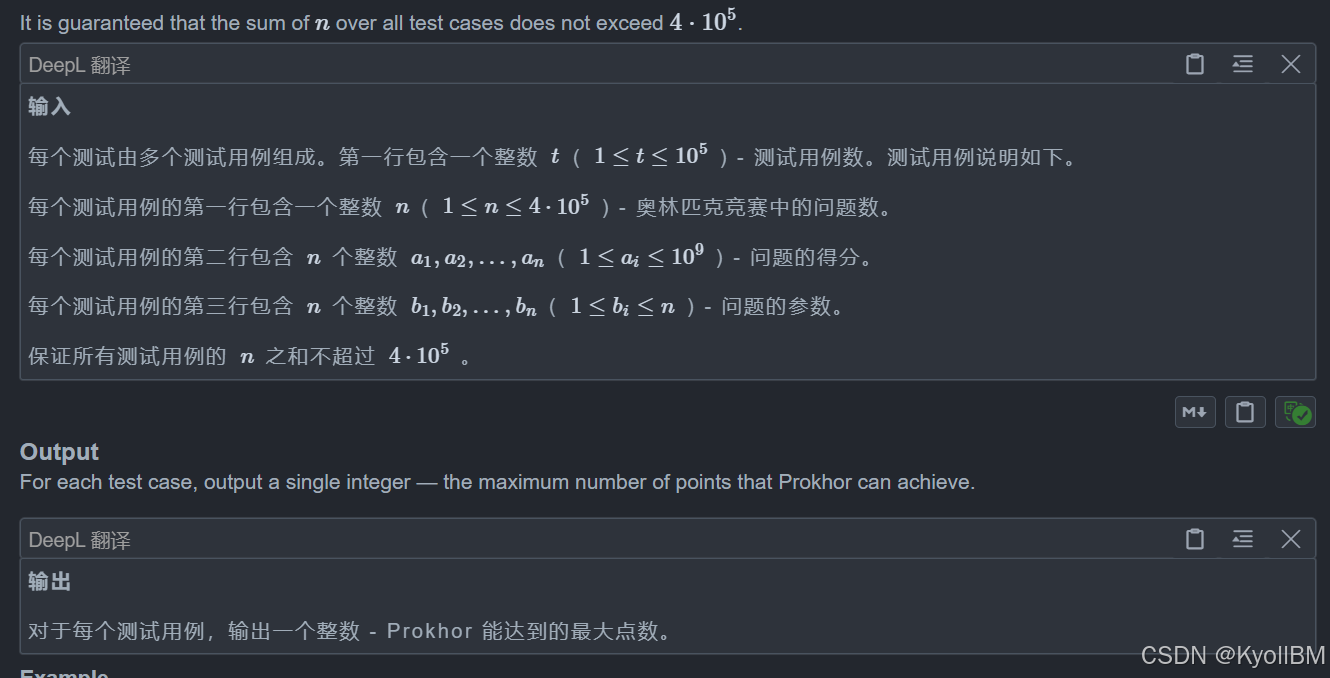
思路：

非常好的题目，看RegenFallen佬的讲解无敌了

这题有两种做法，这里讲dp，我们先来分析一下题目

这题对于任意一个 i 题目我们都有两种选择

第一是写，写了就能获得其积分，然后再从 j < i 的问题中挑一个索引最大的没写过的问题当作下一个问题

第二是不写，如果不写我们就可以从 j < b[i] 的问题中挑一个索引最大的没写过的问题当作下一个问题

我们来简单分析一下，这题对于一个问题我们应该如何选呢，一个显然的思想是贪心，假设我们能跳到 j，那么对于所有 i <= j 的题目我们都能写了，所以最后总和是 sum[j] - cost，即前 j 个问题的总和减去跳到 j 的消耗

那么显然我们可以考虑动态规划，我们定义 dp[i] 为跳到 i 需要的费用，那我们就可以想如何转移了，观察题目对于一个点 i，我们可以跳到所有 j <= b[i] 的点，如果每个数都是一个很大的数，那我们每次的遍历绝对会炸掉，所以我们就要考虑优化

我们可以使用一个小顶堆的优先队列用来存储 “最便宜的跳跃方法”，即一个PII，前一个用于存储其费用，后面用于存储它最大能跳跃到的地方

所以我们就可以这样转移了，我们遍历每一个点 i，如果优先队列里的顶的 second 小于等于 i，说明可以跳到，那么就转移（这样的话肯定是最小花费）否则就丢掉，因为既然小于 i，那么i之后的也用不到了，所以可以丢掉，那么每次转移完我们可以看看这个点能不能跳到后面，如果可以那么就加入到队列中当作一个方案

注意，如果我们队列空了，那么说明就没有方法跳到 i 及其之后的点了，此时我们可以直接跳出循环

代码：

#include <iostream>
#include <algorithm>
#include<cstring>
#include<cctype>
#include<string>
#include <set>
#include <vector>
#include <cmath>
#include <queue>
#include <unordered_set>
#include <map>
#include <unordered_map>
#include <stack>
#include <memory>
using namespace std;
#define int long long
#define yes cout << "YES\n"
#define no cout << "NO\n"
#define PII pair<long long,long long>
void solve()
{
    int n;
    cin >> n;
    vector<int> val(n+1), to(n+1);
    for (int i = 1; i <= n; i++)
    {
        cin >> val[i];
    }
    for (int i = 1; i <= n; i++)
    {
        cin >> to[i];
    }
    vector<int> dp(n + 1, 1e16);
    dp[1] = 0;
    priority_queue<PII, vector<PII>, greater<>> pq;
    pq.push({ 0,1 });//转移到第 1 个的花费是 0
    for (int i = 1; i <= n; i++)
    {
        while (pq.size() && pq.top().second < i) pq.pop();
        if (pq.empty()) break;
        dp[i] = pq.top().first;
        if(to[i] > i)
        pq.push({ pq.top().first + val[i],to[i]});
    }
    int res = 0,sum = 0;
    for (int i = 1; i <= n; i++)
    {
        sum += val[i];
        res = max(res, sum - dp[i]);
    }
    cout << res << endl;
}

signed main()
{
    cin.tie(0)->sync_with_stdio(false);
    int t = 1;
    cin >> t;
    while (t--)
    {
        solve();
    }
    return 0;
}

C. Earning on Bets

题目：

思路：

数学题

 我们可以先假定总和是 S，那么对于每一个点，我们起码要丢 S/ki 个硬币，所以就有

充分必要条件为：\sum S/k[i] < S，为什么是小于呢，因为我们赢得钱要严格大于 S

那么S如何计算呢，由于我们每次投的都要是整数，那么也就是说 S 是每个 k 的倍数，所以我们只需要取 lcm(k1,k2,k3,...) 即可，然后按照上面的条件模拟即可

代码：

#include <iostream>
#include <algorithm>
#include<cstring>
#include<cctype>
#include<string>
#include <set>
#include <vector>
#include <cmath>
#include <queue>
#include <unordered_set>
#include <map>
#include <unordered_map>
#include <stack>
#include <memory>
using namespace std;
#define int long long
#define yes cout << "YES\n"
#define no cout << "NO\n"

int gcd(int a,int b)
{
    return !b ? a : gcd(b, a % b);
}

int lcm(int a,int b)
{
    return a * b / gcd(a, b);
}

void solve()
{
    int n;
    cin >> n;
    vector<int> k(n),res(n);
    for (int i = 0; i < n; i++)
    {
        cin >> k[i];
    }
    if (n == 1) 
    {
        cout << "1\n";
        return;
    }
    int LCM = lcm(k[0],k[1]);
    for (int i = 2; i < n; i++)
    {
        LCM = lcm(LCM, k[i]);
    }
    int tot = 0;
    for (int i = 0; i < n; i++)
    {
        res[i] = LCM / k[i];
        tot += res[i];
    }
    if (tot >= LCM)
    {
        cout << "-1\n";
        return;
    }
    for (auto x : res)
        cout << x << " ";
    cout << endl;
}

signed main()
{
    cin.tie(0)->sync_with_stdio(false);
    int t = 1;
    cin >> t;
    while (t--)
    {
        solve();
    }
    return 0;
}

KyollBM
关注
评论
添加红包

请填写红包祝福语或标题

个

红包个数最小为10个

元

红包金额最低5元

当前余额3.43元 前往充值 >
需支付：10.00元
成就一亿技术人!
领取后你会自动成为博主和红包主的粉丝 规则
hope_wisdom
发出的红包
实付元
使用余额支付
点击重新获取
扫码支付
钱包余额 0

抵扣说明：

1.余额是钱包充值的虚拟货币，按照1:1的比例进行支付金额的抵扣。
2.余额无法直接购买下载，可以购买VIP、付费专栏及课程。

余额充值