【CF】Day20——Codeforces Round 969 (Div. 2) C

C. Dora and C++

题目：

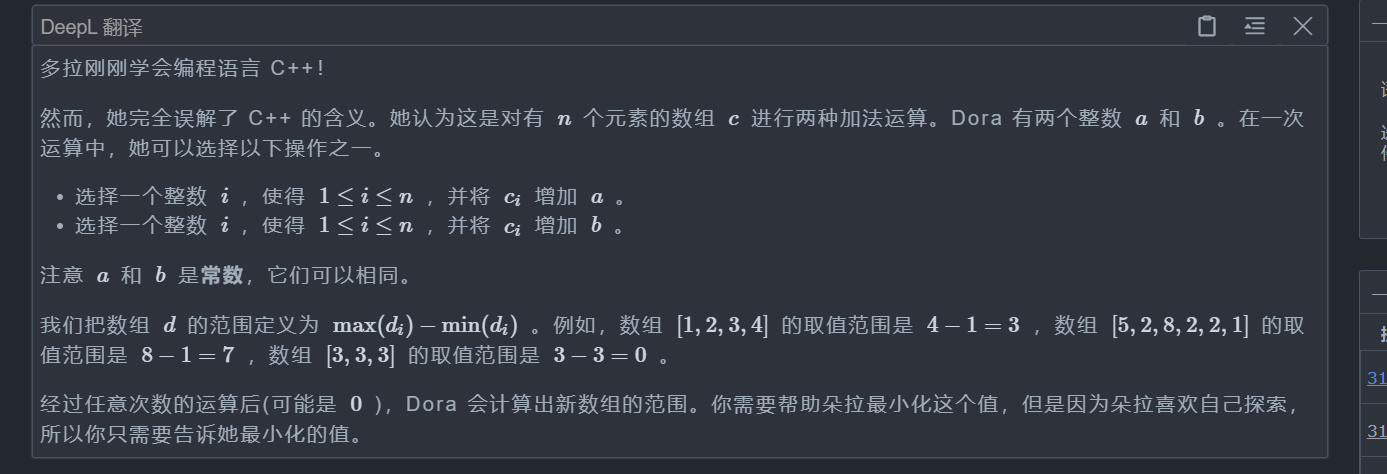
思路：

贝祖定理，又忘了，很好的思维题

这一题可以当一个结论来记忆，结论如下

对于一个数 ai 如果我们可以任意次 +a -a +b -b，那么我们最后一定能得到 ai + k * gcd(a，b)

证明如下：

我们假设当前数为 c 目标值为 d，那么在 x 次 a 操作 和 y 次 b 操作 后，我们得到的结果就是

c + xa + by = d，注意其中 x 和 y 是整数

那么就是 xa + by = d - c，根据贝祖定理，对于这样的方程，我们有解的条件是 gcd(a，b) | d - c

那么观察上面的方程 d - c 不就是每次的增量吗，因此我们一定可以构造出一个 增量 m，使得 m = k * gcd(a，b)，所以我们一定能得到 ai + m 

回到这题，那么由于我们要求 max - min，这里每次只能增加，那我们如何计算呢？

根据上面的结论，我们可以通过无限次的操作使得最后每个 ai 的差距都小于等于 gcd(a，b)，所以这题就变成在 每个数 模 完 gcd(a，b) 后的意义下，求 max - min

所以我们可以这样操作，在模完后排序数组，然后我们尝试将每个数都加上 g 后看看新的差值是多少，因为模完后每个数都小于 gcd(a，b)，所以我们如果让第一个数加上 g ，那么这个数就会变成最大的数，而最小的数就会变成原来最小的数后面的那个数

比如 1 3 5 6 10 g=11，当1加上11后，12就是最大值，而3变成了最小值

因此我们这样模拟一下即可，注意一开始要初始化答案为最开始的最大值减最小值

代码：

#include <iostream>
#include <algorithm>
#include<cstring>
#include<cctype>
#include<string>
#include <set>
#include <vector>
#include <cmath>
#include <queue>
#include <unordered_set>
#include <map>
#include <unordered_map>
#include <stack>
#include <memory>
using namespace std;
#define int long long
#define yes cout << "YES\n"
#define no cout << "NO\n"

int gcd(int a, int b)
{
    return !b ? a : gcd(b, a % b);
}

void solve()
{
    int n, a, b;
    cin >> n >> a >> b;
    vector<int> A(n+1);
    int g = gcd(a, b);
    for (int i = 1; i <= n; i++)
    {
        cin >> A[i];
        A[i] %= g;
    }
    sort(A.begin()+1, A.end());
    int ans = A[n] - A[1];
    for (int i = 1;i < n;i++)
    {
        ans = min(ans, A[i] + g - A[i + 1]);
    }
    cout << ans << endl;
}

signed main()
{
    cin.tie(0)->sync_with_stdio(false);
    int t = 1;
    cin >> t;
    while (t--)
    {
        solve();
    }
    return 0;
}