B. Milena and Admirer
题目:


思路:
想到了,但是代码细节没处理好
既然我们要将数组变成升序,并且要求最小值,那么肯定要贪心一点
我们可以从后开始枚举每一个数,同时定义一个mx代表数组的最大值,如果当数小于mx,说明符合,就不需要更改,同时将mx变为这个数,反之肯定要将这个数进行操作了,同时将mx变为操作后的数
思路是这样,那么如何实现呢?
首先我们要分解的话肯定是尽量分成较大的数,比如5分成2和3,8分成4和4,那么如何分呢?
我们可以利用mx,首先肯定是要分解成小于或等于mx的数,假设要分成k份
那么就是有 [x/k] <= mx,其中[]代表向上取整,因为比如5,分成两份是2和3,我们要保证较大值也要小于mx,那么转化一下式子,就是 [x / mx] <= k 那我们要尽量少切,也就是取等号即可,那么mx要变为什么呢?其实就是 【x / k】其中【】代表向下取整,还是5,假如我们要分成两份,那么新的最大值要取较小的值,即2,那么切的次数就是k-1次,最后答案就是所有k-1的和
至此题目解决完毕,上代码
代码:
#include <iostream>
#include <algorithm>
#include<cstring>
#include<cctype>
#include<string>
#include <set>
#include <vector>
#include <cmath>
#include <queue>
#include <unordered_set>
#include <map>
#include <unordered_map>
#include <stack>
#include <memory>
using namespace std;
#define int long long
#define yes cout << "YES\n"
#define no cout << "NO\n"
void solve()
{
int n;
cin >> n;
vector<int> a(n);
for (int i = 0; i < n; i++)
{
cin >> a[i];
}
int maxn = a[n - 1],res = 0;
for (int i = n-1; i >= 0; i--)
{
if (a[i] <= maxn)
{
maxn = a[i];
}
else
{
int k = (a[i] + maxn - 1) / maxn;
maxn = a[i] / k;
res += k - 1;
}
}
cout << res << endl;
}
signed main()
{
cin.tie(0)->sync_with_stdio(false);
int t = 1;
cin >> t;
while (t--)
{
solve();
}
return 0;
}
C. Colorful Grid
题目:
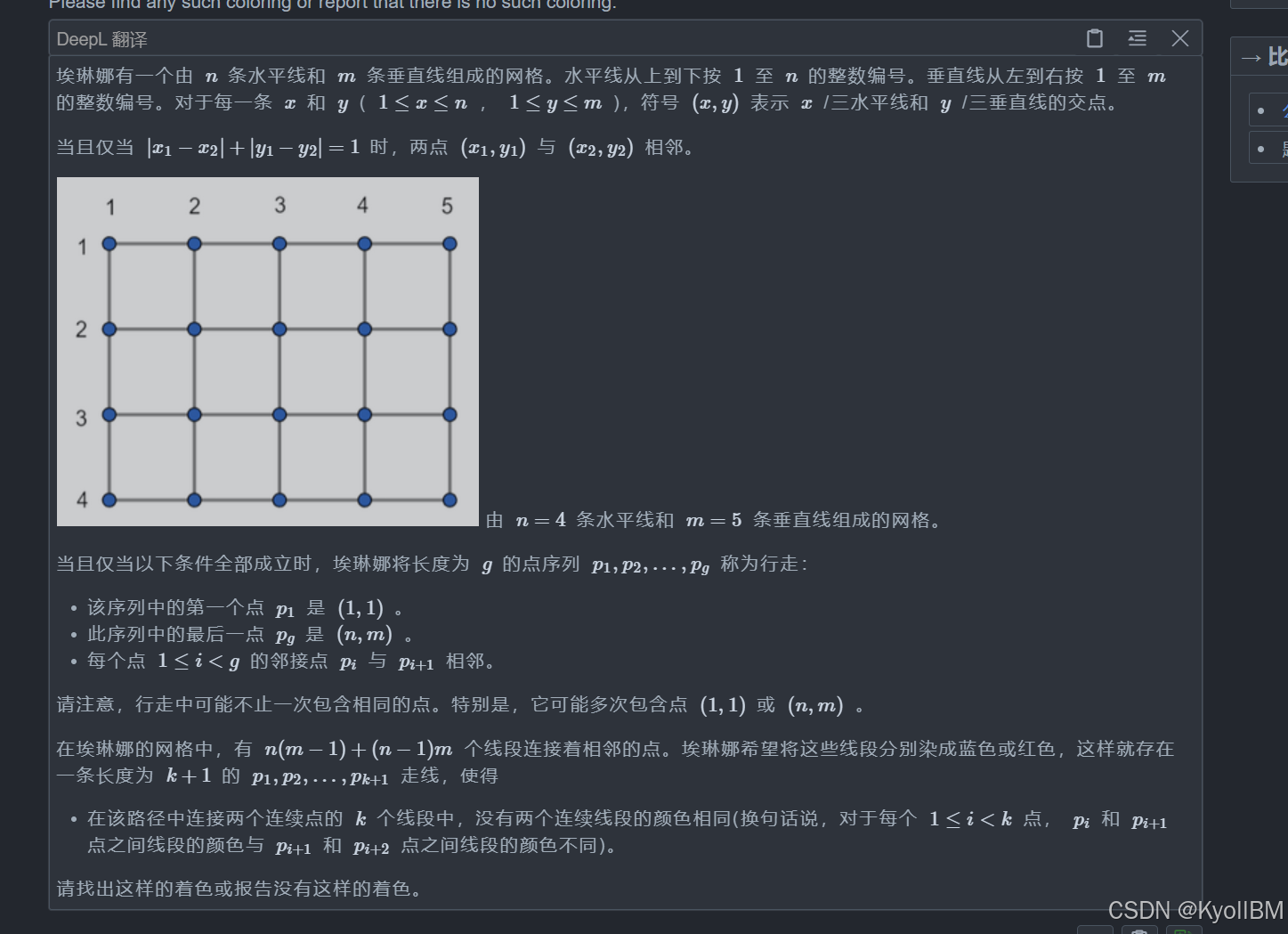

思路:
小清新构造,很有意思
首先我们要考虑什么情况不存在解决方案
既然要从(1,1)走到(n,m)那么最少的步数就是 n+m-2 也就是说如果步数小于这个,那肯定不行,那么再看如果大于呢?
我们发现题目说同一个点是可以重复走的,那么我们是否可以构造出一个环呢?显然是可行的
只要我们构造出一个最小环,那么我们就能在环上一直走,其长度是4
也就是说只要 (k - (n+m-2))% 4 == 0 ,就说明这个情况也能构造出来,那么还有什么可能吗?
其实还有一种,除了走直线,我们还能走曲线,我们可以构造出一个拐弯,这样就能比走直线多走两步,也就是说 (k - (n+m-2))% 4 == 2 的情况也是可行的
可以证明,除此自外没有任何情况可以构造了,那么我们如何构造呢?
可以参考cf的官方方法,首先肯定要有一条可以走到重点的路,然后再构造出一个环,同时再构造出一个拐弯,那我们就可以像下图这样构造了

至此解决完毕,实现上就是打表,注意奇偶性即可
代码:
#include <iostream>
#include <algorithm>
#include<cstring>
#include<cctype>
#include<string>
#include <set>
#include <vector>
#include <cmath>
#include <queue>
#include <unordered_set>
#include <map>
#include <unordered_map>
#include <stack>
#include <memory>
using namespace std;
#define int long long
#define yes cout << "YES\n"
#define no cout << "NO\n"
void solve()
{
int n, m, k;
cin >> n >> m >> k;
vector<vector<char>> mpn(n-1, vector<char>(m, 'B'));
vector<vector<char>> mpm(n, vector<char>(m-1, 'B'));
int minn = n + m - 2;
if (k < minn)
{
no;
return;
}
if ((k - minn) % 4 != 2 && (k - minn) % 4 != 0)
{
no;
return;
}
yes;
for (int i = 0; i < m-1; i++)
{
if ((i & 1) == 0)
mpm[0][i] = 'R';
}
mpm[1][0] = 'R';
for (int i = 0; i < n - 1; i++)
{
if (mpm[0][m - 2] == 'R' && (i & 1))
{
mpn[i][m - 1] = 'R';
}
else if (mpm[0][m - 2] != 'R' && (i & 1)==0)
mpn[i][m - 1] = 'R';
}
if (mpn[n - 3][m - 1] == 'R')
{
mpn[n - 2][m - 2] = 'R';
}
else
{
mpm[n - 2][m - 2] = 'R';
mpm[n - 1][m - 2] = 'R';
}
for (int i = 0; i < n; i++)
{
for (int j = 0; j < m - 1; j++)
{
cout << mpm[i][j] << " ";
}
cout << endl;
}
for (int i = 0; i < n-1; i++)
{
for (int j = 0; j < m; j++)
{
cout << mpn[i][j] << " ";
}
cout << endl;
}
}
signed main()
{
cin.tie(0)->sync_with_stdio(false);
int t = 1;
cin >> t;
while (t--)
{
solve();
}
return 0;
}D. Absolute Beauty
题目:


思路:
思路远大于实现,数形结合
对于这种绝对值的题目,我们一般考虑的是变化的量,即如何让交换后的改变量最大,那我们来分析一下题目
我们可以画出下图

我们将数字在数轴上表示,那么奉献就是线段长度,其中红色是没交换前的奉献,蓝色是交换后的奉献(这里只画了几种情况)
我们其实可以发现,只有当两个区间不相交时,交换bi和bj才会增加奉献,那么我们只需要储存最远的不相交的两个区间即可,那么储存什么值呢?
可以发现,增加的奉献就是左区间的右端点 r,和右区间的左端点 l 的差的两倍,即 2 * (l - r)
所以我们遍历整个数组,每次都加上其原来的奉献,同时储存所有区间的最小右端点,和所有区间的最大左端点既可,最后看看到底要不要交换
具体看代码
代码:
#include <iostream>
#include <algorithm>
#include<cstring>
#include<cctype>
#include<string>
#include <set>
#include <vector>
#include <cmath>
#include <queue>
#include <unordered_set>
#include <map>
#include <unordered_map>
#include <stack>
#include <memory>
using namespace std;
#define int long long
#define yes cout << "YES\n"
#define no cout << "NO\n"
void solve()
{
int n;
cin >> n;
vector<int> a(n), b(n);
for (int i = 0; i < n; i++)
{
cin >> a[i];
}
for (int i = 0; i < n; i++)
{
cin >> b[i];
}
int ans = 0;
int r = 1e9, l = 0;
for (int i = 0; i < n; i++)
{
r = min(r, max(a[i], b[i]));
l = max(l, min(a[i], b[i]));
ans += abs(a[i] - b[i]);
}
cout << max(ans,ans + 2 * (l - r)) << endl;
}
signed main()
{
cin.tie(0)->sync_with_stdio(false);
int t = 1;
cin >> t;
while (t--)
{
solve();
}
return 0;
}C. Anji's Binary Tree
题目:


思路:
一道很简单的题,想复杂了,还是对dfs的用法不够理解
翻译一下题目:给定一颗有根树(根为1),每个节点都有一个操作,分别为U,L,R,分别代表往父节点走,往左子节点走,往右子节点走,现在我们从根节点出发,每次都按节点的操作行走,问最少要多少次 改变节点的操作(如将L改为R) 才能走到叶子节点
一开始我是直接统计走到每一个叶子节点需要什么操作,然后将这个操作与原树的操作对比,需要改变的次数就是不同的地方,但是这样的话最后内存超了,所以不行,那么我们按照这个思路重新写一遍看看呢
还是一样的,首先肯定要找到叶子节点的路,还是要用dfs,那么对于任意一个节点,只要他有子孩子,那我们就要往下走,既然我们要求改变操作的次数,那我们直接走过每一条路,然后看那条路的改变次数最小就行了,那么如何计算需要改变的次数呢?
看下图

如果我们按其节点的操作走,肯定是走不到叶子节点的,一个很显然的最小操作数是将1的操作改为R,这样只需要一次操作就能走到节点3,那我们如何写呢?
很简单,对于节点s,如果我们往左走,如果string[s]不为L,那么就要加一次改变次数,如果是L,那么就不用加,以此类推,这样就变成递归的形式了,然后每次对左右两次操作取最小值即可
具体实现看代码
代码:
#include <iostream>
#include <algorithm>
#include<cstring>
#include<cctype>
#include<string>
#include <set>
#include <vector>
#include <cmath>
#include <queue>
#include <unordered_set>
#include <map>
#include <unordered_map>
#include <stack>
#include <memory>
using namespace std;
#define int long long
#define yes cout << "YES\n"
#define no cout << "NO\n"
struct Node
{
int l = -1, r = -1;
};
int n;
string s;
int dfs(const vector<Node>& Tree, int self)
{
if (!self)
return 1e9;
if (Tree[self].l == 0 && Tree[self].r == 0)
return 0;
return min((s[self] != 'L') + dfs(Tree, Tree[self].l), (s[self] != 'R') + dfs(Tree, Tree[self].r));
}
void solve()
{
cin >> n;
cin >> s;
s = '$' + s;
vector<Node> tree(n + 1);
for (int i = 1; i <= n; i++)
{
int l, r;
cin >> l >> r;
tree[i].l = l;
tree[i].r = r;
}
cout << dfs(tree, 1) << endl;
}
signed main()
{
cin.tie(0)->sync_with_stdio(false);
int t = 1;
cin >> t;
while (t--)
{
solve();
}
return 0;
}D. Small GCD
题目:


思路:
好题,好题,好题
首先分析题目,我们要找出一个三元组a,b,c,然后求两个较小值的gcd,也就是最大值是什么无所谓,我们只考虑最小值
那么这题就变成求所有 gcd(a,b) 的奉献和,任意一个 gcd(a,b)的奉献和就是 gcd(a,b) * 数组中大于max(a,b)的数的数量
如1 2 3 5,如果要求gcd(1,2)的奉献,显然就是 gcd(1,2) * 2,因为2后有两种选择,即3 5
所以我们就不需要考虑原数组到底啥样了,我们直接一个排序即可
但是如果这样一个一个算的话肯定会超时,那么我们如何优化呢?
遇到这种题我们可以考虑每个数的奉献,由于是求gcd,那么我们可以转化为每个因子在答案中的奉献
观察到a的数据只有1e5,那我们就可以预处理1e5中每个数的因子有多少以及分别是什么
我们定义一个 f[i] ,其代表的是以因子 i 为gcd能组成的对数,即 f[i] += cnt[i] * (n - pos),其中pos为因子i对于的数a在数组中的位置,cnt[i] 代表之前有出现过多少次 i
让我们来理解一下为什么是这样子,比如对于数组 2 4 8 ... 遇到 2 时,其因子有 1 2
那么f[1] = 0 * (n - 1),f[2] = 0 * ( n- 1),因为此前我们没有遇到过1 2,所以都是0,当我们处理完因子的奉献后,再将cnt[1]++,cnt[2]++,顺序很重要
之后遇到4,还是一样的操作,不过由于此时 1 2 出现过,所以1 2的奉献就要增加了,以此类推,最后所有数都被找过一遍了
我们来分析一下为什么要选所有因子,难道不是选最大因子就行了吗?
因为我们要求所有的 gcd(a,b),如上面,对于2,我们要求 gcd(2,4) + gcd(2,8) + ... ,如果只考虑最大因子,那么如果后面出现了一个数使得其 gcd(2,x) == 1 的话,那么因子1的奉献应该要增加,但是我们没考虑,所以答案就会出错了
通俗的讲,我们每一种因子都有可能在后面遇到,所以我们所有因子都要考虑
那么还有一点显而易见,就是会重复计算,比如 2 4 8,其中因子2被重复计算了,如4 8,他们的gcd是4,但是我们算的时候会把 2 也算进去,因为他们都有因子2,所以我们要考虑去重
这里根据容斥原理,一个因数的奉献 = 现在的奉献减去其所有倍数的奉献 = 其真正的奉献
如 2 4 8,因数 2 的奉献就是 gcd(2 4) 和 gcd(2 8),但是计算过程中 2 却有3个,其原因就是4和8的gcd应该是4,但是此时2也被算过一遍了,所以要减去所有2的倍数的贡献,因为此时2的贡献其实是0,或者可以这样理解,我们要选 4,但是我们把 2 也都选了,所以 2 的奉献就多了,而这多的部分都在 4 里,所以减去 4 的奉献即可,这样就只剩 2 的奉献了
具体细节看代码
代码:
#include <iostream>
#include <algorithm>
#include<cstring>
#include<cctype>
#include<string>
#include <set>
#include <vector>
#include <cmath>
#include <queue>
#include <unordered_set>
#include <map>
#include <unordered_map>
#include <stack>
#include <memory>
using namespace std;
#define int long long
#define yes cout << "YES\n"
#define no cout << "NO\n"
const int MAXN = 1e5;
vector<vector<int>> factor(MAXN + 5);
void solve()
{
int n;
cin >> n;
vector<int> a(n+1);
vector<int> f(MAXN + 5, 0);
vector<int> cnt(MAXN + 5, 0);
for (int i = 1; i <= n; i++)
{
cin >> a[i];
}
sort(a.begin()+1, a.end());
for (int i = 1; i <= n; i++)
{
for (auto fac : factor[a[i]])
{
f[fac] += cnt[fac] * (n - i);
cnt[fac]++;
}
}
int res = 0;
for (int i = MAXN; i; i--)
{
for (int j = i*2; j <= MAXN; j+=i)
{
f[i] -= f[j];
}
res += f[i] * i;
}
cout << res << endl;
}
signed main()
{
for (int i = 1; i <= MAXN; i++)
{
for (int j = i; j <= MAXN; j+=i)
{
factor[j].push_back(i);
}
}
cin.tie(0)->sync_with_stdio(false);
int t = 1;
cin >> t;
while (t--)
{
solve();
}
return 0;
}























 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








