【CF】Day2

最新推荐文章于 2025-05-20 19:46:55 发布
最新推荐文章于 2025-05-20 19:46:55 发布
阅读量797 收藏 15
点赞数 25
文章标签： 算法 c++ 数据结构
版权声明：本文为博主原创文章，遵循 CC 4.0 BY-SA 版权协议，转载请附上原文出处链接和本声明。
本文链接：https://blog.youkuaiyun.com/qq_61422664/article/details/146130514
版权

思维题

当你认为这道题很难的时候你就输了，对于思维题我们可以考虑从数据下手，或者缩减情况，从特殊再到一般

D. Harder Problem

题目：

思路：

我们可以知道，如果任意两个数字数字出现次数相同，那么肯定可以当作这个序列的模，也就是说对于一个数列1~n，其中任意一个数字都可以当作这个序列的模，因为他们都只出现过一次，所以我们可以构造一个排列，由于数组长度刚好是n，所以满足每个元素都可出现过一次

于是可以根据bi来构造了，我们可以按bi中数字出现的顺序把数字都放在前面，没出现过的数字直接排在后面即可，详见代码

代码：

#include <iostream>
#include <algorithm>
#include<cstring>
#include<cctype>
#include<string>
#include <set>
#include <vector>
#include <cmath>
#include <queue>
#include <unordered_set>
#include <map>
#include <unordered_map>
#include <stack>
#include <memory>
using namespace std;
#define ll long long
#define yes cout << "YES" << endl
#define no cout << "NO" << endl

void solve()
{
    int n;
    cin >> n;
    vector<int> a;
    set<int> has;
    for (int i = 0; i < n; i++)
    {
        int x;
        cin >> x;
        if (!has.count(x))
        {
            a.push_back(x);
        }
        has.insert(x);
    }
    set<int> dnthas;
    for (int i = 1; i <= n; i++)
    {
        if (!has.count(i))
            dnthas.insert(i);
    }
    for (auto x : a)
    {
        cout << x << " ";
    }
    for (auto d : dnthas)
    {
        cout << d << " ";
    }
    cout << endl;
}

int main()
{
//    cin.tie(0)->sync_with_stdio(false);
    int t = 1;
    cin >> t;
    while (t--)
    {
        solve();
    }
    return 0;
}

https://codeforces.com/problemset/problem/1971/D

https://codeforces.com/problemset/problem/1971/D

D. Binary Cut

题目：

思路：

题目要求我们将字符串最后排成000...01111..11的形式，那么显然我们肯定要将所有连续段落拆开，但是我们观察题目给的样例发现，它只切了3份，这其实也是一个提示，我们可以将一个01有拼接的串合成一整块，这样就能少切一刀，同时有且仅有少切一次，因为01 和 01是无法直接拼起来的

代码：

#include <iostream>
#include <algorithm>
#include<cstring>
#include<cctype>
#include<string>
#include <set>
#include <vector>
#include <cmath>
#include <queue>
#include <unordered_set>
#include <map>
#include <unordered_map>
#include <stack>
#include <memory>
using namespace std;
#define ll long long
#define yes cout << "YES" << endl
#define no cout << "NO" << endl

void solve()
{
    string s;
    cin >> s;
    int tag = 0;
    int cnt = 1;
    char now = s[0];
    for (int i = 1; i < s.length(); i++)
    {
        if (s[i] != now)
        {
            now = s[i];
            cnt++;
        }
        if (s[i] == '1' && s[i-1] == '0')
        {
            tag = 1;
        }
    }
    cout << cnt - tag << endl;
}

int main()
{
//    cin.tie(0)->sync_with_stdio(false);
    int t = 1;
    cin >> t;
    while (t--)
    {
        solve();
    }
    return 0;
}

C. Assembly via Remainders

题目：

 

思路：

我们可以观察一下数据范围，居然只有500！那我们就可以想到可以用一个很大的数来构造这个数列了，对于a1，我们可以选501，这样即使x是500，我们的余数也是500（500 / 501 = 0 ... 500）

所以后面的同理，我们就可以使a2 = a1 + x1，总之每次都是前一个数+当前的X，因为除数大于大于被除数，所以最后肯定的余数肯定是被除数

代码：

#include <iostream>
#include <algorithm>
#include<cstring>
#include<cctype>
#include<string>
#include <set>
#include <vector>
#include <cmath>
#include <queue>
#include <unordered_set>
#include <map>
#include <unordered_map>
#include <stack>
#include <memory>
using namespace std;
#define ll long long
#define yes cout << "YES" << endl
#define no cout << "NO" << endl

void solve()
{
    int n;
    cin >> n;
    n--;
    int a = 501;
    cout << a << ' ';
    while (n--)
    {
        int x;
        cin >> x;
        a += x;
        cout << a << ' ';
    }
    cout << '\n';
}

int main()
{
//    cin.tie(0)->sync_with_stdio(false);
    int t = 1;
    cin >> t;
    while (t--)
    {
        solve();
    }
    return 0;
}

B. Olya and Game with Arrays

题目：

 

思路：

对于这道题，我们肯定可以先想到对每队排好序，那观察题目给的条件，我们可以知道其实最后的答案取决与每个数组的最小值和次小值，那么贪心的想，我们肯定全选次小值是最好的，但是由于每次都要将最小值移走，所以我们肯定要用一个数组来装其他数组的最小值，很显然，我们要装的数组就是次小值最小的数组上，这样就能牺牲最小而得到最大

注意，当我们把其他数组的最小值移走后，那个次小值最小的数组的最小值可能会发生变化，所以还得维护所有数组最小值中的最小值

于是答案就是 次小值的和 + 最小值的最小值 - 次小值的最小值

代码：

#include <iostream>
#include <algorithm>
#include<cstring>
#include<cctype>
#include<string>
#include <set>
#include <vector>
#include <cmath>
#include <queue>
#include <unordered_set>
#include <map>
#include <unordered_map>
#include <stack>
#include <memory>
using namespace std;
#define ll long long
#define yes cout << "YES" << endl
#define no cout << "NO" << endl

void solve()
{
    int n;
    cin >> n;
    vector<vector<int>> a(n);
    ll ans = 0;
    for (int i = 0; i < n; i++)
    {
        int m;
        cin >> m;
        for (int j = 0; j < m; j++)
        {
            int x; cin >> x;
            a[i].push_back(x);
        }
        sort(a[i].begin(), a[i].end());
        ans += a[i][1];
    }
    sort(a.begin(), a.end(), [](vector<int> a, vector<int> b) {
        return a[0] < b[0]; });
    int minf = 1e9;
    int ming = 1e9;
    for (int i = 0; i < n; i++)
    {
        minf = min(minf, a[i][0]);
        ming = min(ming, a[i][1]);
    }
    cout << ans + minf - ming << endl;
}

int main()
{
//    cin.tie(0)->sync_with_stdio(false);
    int t = 1;
    cin >> t;
    while (t--)
    {
        solve();
    }
    return 0;
}

C. Yet Another Permutation Problem

题目：

思路：

其实我们可以观察发现，最后的答案一定是[n/2]，为什么呢？

对于n，我们只需要找到n/2，这样就能有gcd(n,n/2) = n/2这个答案了

同理对于其他 n-1,n-2...，我们都能找到对于的数字，直到1，同时可以确保每个gcd都不相同，因为每次gcd都是n/2，而每次取得n都不一样，所以这个方法肯定是最优得

所以我们每次都可以用x去寻找2*x，同时每次找不到后都让x+2，为什么呢？

因为偶数都被x=2找过了，所以接下来我们只需要找奇数就行了

代码：

#include <iostream>
#include <algorithm>
#include<cstring>
#include<cctype>
#include<string>
#include <set>
#include <vector>
#include <cmath>
#include <queue>
#include <unordered_set>
#include <map>
#include <unordered_map>
#include <stack>
#include <memory>
using namespace std;
#define ll long long
#define yes cout << "YES" << endl
#define no cout << "NO" << endl

void solve()
{
    int n;
    cin >> n;
    vector<int> a(n);
    int cur = 0;
    for (int i = 1; i <= n; i += 2) {
        for (int j = i; j <= n; j *= 2) {
            a[cur++] = j;
        }
    }
    for (int i = 0; i < n; ++i) {
        cout << a[i] << " ";
    }
    cout << '\n';
}

int main()
{
    //cin.tie(0)->sync_with_stdio(false);
    int t = 1;
    cin >> t;
    while (t--)
    {
        solve();
    }
    return 0;
}

B. Split Sort

题目：

 

思路：

这是一个比较考直觉得思维题，对于任意一个x，如果x+1在x前面，那我们肯定只能用x+1来使x到x+1前，所以我们只需要找有多少个这种情况即可

官方题解也没证明，我只能说观察力惊人（

代码：

#include <iostream>
#include <algorithm>
#include<cstring>
#include<cctype>
#include<string>
#include <set>
#include <vector>
#include <cmath>
#include <queue>
#include <unordered_set>
#include <map>
#include <unordered_map>
#include <stack>
#include <memory>
using namespace std;
#define ll long long
#define yes cout << "YES" << endl
#define no cout << "NO" << endl
const int maxn = 1e5 + 5;
int t, n, a[maxn], ans, x[maxn];
void solve()
{
	ans = 0;
	cin >> n;
	for (int i = 1; i <= n; i++) {
		cin >> a[i];
		x[a[i]] = i;
	}
	for (int i = 1; i < n; ++i) {
		ans += (x[i] > x[i + 1]);
	}
	cout << ans << endl;
}

int main()
{
//    cin.tie(0)->sync_with_stdio(false);
    int t = 1;
    cin >> t;
    while (t--)
    {
        solve();
    }
    return 0;
}

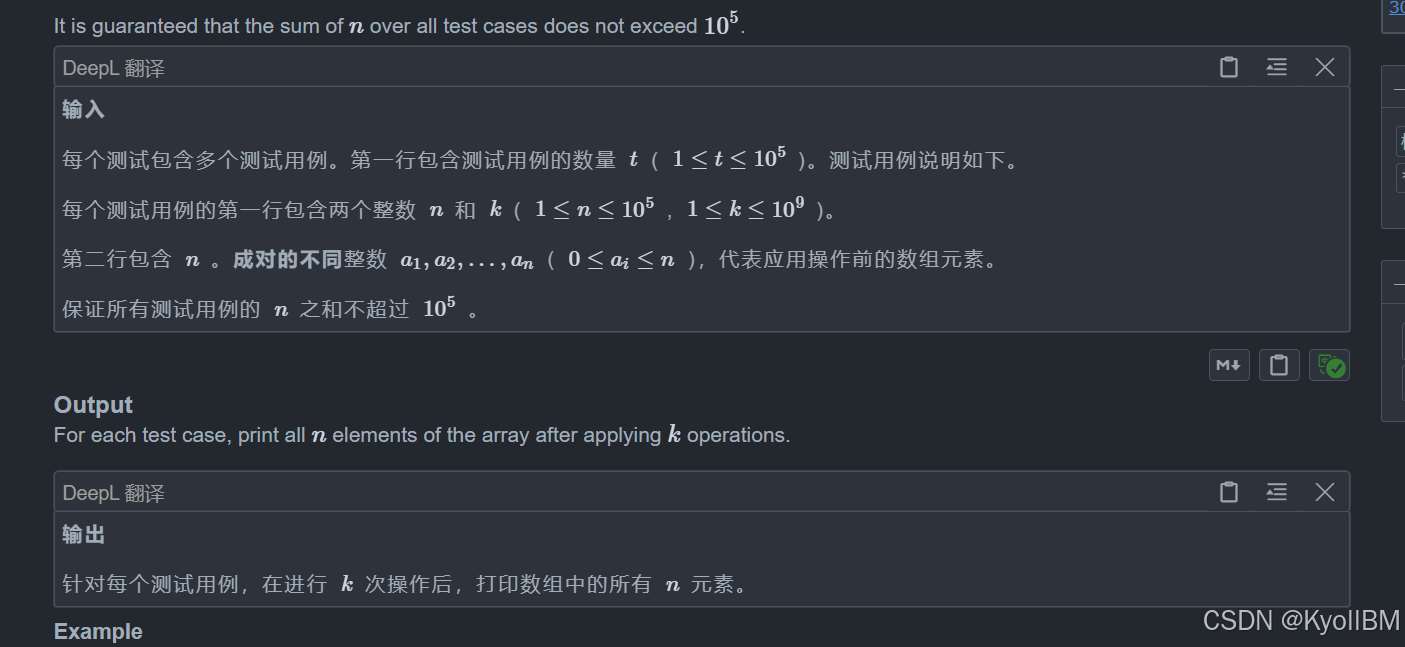
C. MEX Repetition

题目：

 

思路：

观察题目给的数据，k足足有1e9，那么就算模拟来做，最后肯定也是超时，所以我们就要来找规律，对于这种大数据得题目，我们第一眼肯定要往循环情况上找

观察样例 1 2 3 4 5，我们接下来把每次操作一开始的MEX写下来

1. 1 2 3 4 5 | 0

2. 0 1 2 3 4 | 5

3. 5 0 1 2 3 | 4

4. 4 5 0 1 2 | 3

5. 3 4 5 0 1 | 2

6. 2 3 4 5 0 | 1

7. 1 2 3 4 5 | 0

这时我们发现进入了循环，且循环的周期T = n+1

同时我们再观察一下，我们可以发现每次都是在改变循环的起点和终点的位置

比如2.就是将起点从0开始终点以4结束，那我们就只需要计算这个区间即可

代码：

#include <iostream>
#include <algorithm>
#include<cstring>
#include<cctype>
#include<string>
#include <set>
#include <vector>
#include <cmath>
#include <queue>
#include <unordered_set>
#include <map>
#include <unordered_map>
#include <stack>
#include <memory>
using namespace std;
#define ll long long
#define yes cout << "YES" << endl
#define no cout << "NO" << endl

const int N = 1e5 + 5;
int n;
int a[N];
int cnt[N];
void init()
{
	for (int i = 0; i <= n; i++)
	{
		cnt[i] = 0;
	}
}
void solve()
{
	int k;
	cin >> n >> k;
	init();
	int mex = 0;
	for (int i = 1; i <= n; i++)
	{
		cin >> a[i];
		cnt[a[i]]++;//记录每个数字是否出现
	}
	for (int i = 0; i <= n; i++)
	{
		if (!cnt[i])
		{
			mex = i;//找到当前的MEX
			break;
		}
	}
	a[n + 1] = mex;
	k = k % (n + 1);
	for (int i = n + 1 - k + 1; i <= n + 1; i++)
	{
		cout << a[i] << " ";
	}
	for (int i = 1; i <= n - k; i++)
	{
		cout << a[i] << " ";
	}
	cout << endl;
}
int main()
{
//    cin.tie(0)->sync_with_stdio(false);
    int t = 1;
    cin >> t;
    while (t--)
    {
        solve();
    }
    return 0;
}

KyollBM
关注
cf 1199A A. City Day
dream_it_的博客
08-01 294
A. City Day time limit per test1 second memory limit per test256 megabytes inputstandard input outputstandard output For years, the Day of city N was held in the most rainy day of summer. New mayor de...
CF757G Can Bash Save the Day? 题解
莫莫 dicol 的博客
08-31 172
CF757G Can Bash Save the Day? 时间复杂度分析好题（大雾）。 将询问拆成几部分，也就是 dis(u,v)=dep(u)+dep(v)−2∗dep(Lca(u,v))dis(u, v) = dep(u) + dep(v) - 2 * dep(Lca(u, v))dis(u,v)=dep(u)+dep(v)−2∗dep(Lca(u,v))。 显然对于 LcaLcaLca 我们直接进行树链剖分即可。 我们对于每一个 vvv 维护 ≤l\le l≤l 的 dep(Lca)dep(Lc
C. Boring Day（cf955）
m0_74310050的博客
07-05 606
题意：每次可以从数组顶端取任意数量，取出的所有数组之和如果在l到r之间，则获胜，否则失败，求最大获胜局数。分析：用双指针算出区间内的和。
CF 1982C - Boring Day
weixin_47774773的博客
10-13 470
【代码】CF 1982C - Boring Day。
ZJUT12 Day2
Lecxcy的博客
10-02 2090
ZJUT12 Day1 1、CF 963A Alternating Sum tags：数学 一开始观察式子想到左右同乘(a−b)(a-b)(a−b)。因为(a−b)Σi=0nan−ibi=an+1−bn+1(a-b)\Sigma_{i=0}^na^{n-i}b^i=a^{n+1}-b^{n+1}(a−b)Σi=0n​an−ibi=an+1−bn+1。 然后发现化简出来的结果是s0an+1−snbn+1+Σi=0n−1(si+1−si)an−ibi+1s_0a^{n+1}-s_nb^{n+1}+\Sigma_
day2
zhoumengyang1993的博客
08-25 192
1.质数判断问题 http://naotu.baidu.com/file/c154a14e74903266cfeddaa50acb80cf?token=2d4b529dbddb2de6
CF757B Bash‘s Big Day
weixin_44021857的博客
08-22 68
【代码】CF757B Bash‘s Big Day。
【CF】Day43——Codeforces Round 906 (Div. 2) E1
qq_61422664的博客
04-25 598
very好题，加深对扫描线的应用，值得深思由于k = 2，那我们就可以使用简单一点的方法来写题目可以转化为：给定n个线段，现在让你删去2条线段，使得没有与线段相交的点数最多那么首先明确一点，就是只有下雨在 0 ~ 2 的城市才可能造成奉献，否则是不可能造成奉献的，因为这个城市起码与三个线段相交，我们只删两个是没用的那么对于这种区间变化的题目，我们首先想到的就是差分数组+扫描线题目的答案肯定是： 本来就是 0 的城市 + 删去 2 条线段后的新的为 0 城市。
day2-基于user-based CF的电影预测评分实现
cpy52349119的博客
12-07 830
基于user-based CF的电影预测评分代码实现
NOI金牌冲刺day2
woshitiancai100的博客
04-30 115
APIO CF比赛
【CF gym 103260】40th Petrozavodsk Programming Camp, Day 5，2021.2.3 水题2题
小哈里的博客
10-17 2282
M、Discrete Logarithm is a Joke 题意： 思路： 不难想到an=g^{an+1},因为样例给了 a[1000000]的值，所以反着推就行了。 记得开int128，longlong会爆，也不要用浮点数表示整数，double会爆，提交的时候选G++20，不然编译器会爆。 #include<bits/stdc++.h> using namespace std; const int maxn = 1e6+10; typedef __int128 LL; inline
cftime-1.6.3-cp310-cp310-win_amd64.whl.zip
02-22
2. **日期和时间类**：提供了与`datetime`模块类似的API，但可以处理非标准日历，比如gregorian、noleap、365_day、all_leap等。 3. **与netCDF库的兼容性**：在处理netCDF文件时，可以自动转换时间坐标，方便数据...
Linux云计算 |【第四阶段】NOSQL-DAY2
小安的运维专栏
09-26 1520
Redis集群概述、部署Redis集群（配置manage管理集群主机、创建集群、访问集群、添加节点、移除节点）
a【思维题】山东集训day9T1：CF991D Bishwock
ZYzyZzzz的博客
11-13 330
这是一道原题，地址如下： CF991D Bishwock A 题目描述 给一个2×n2\times n2×n的网格，上面一些位置以及被覆盖上了 现在你有一种形状为L的小块，每个由三个小格组成，构成L型 现在问你，当前的网格最多还能摆多少小块（不能覆盖以及覆盖过的格子） 输入格式 两行两个字符串由X,.组成，X表示被覆盖了，.表示还没有 输出格式 一行一个整数 样例 样例输入 00X00X0XXX0...
黑马Java基础笔记-13常用查找算法
最新发布
IKUNIKUNIKUNikun的博客
05-20 308
数学表达αnmαmn​，其中nnn为哈希表中当前元素数，mmm为桶的总数或槽位总数。意义：表示哈希表的“填充率”，负载因子高意味着更多的键映射到相同或相邻的位置，冲突概率也随之升高，从而增大查找或插入时的探测或链表长度。再哈希是指在哈希表运行过程中，检测到负载因子α\alphaα达到或超过预设阈值后，动态地创建一个更大的新表（通常容量翻倍），并将旧表中所有元素按照新表大小重新计算哈希并插入新表的过程。这一过程又称“扩容”（resize）或“重散列”，旨在降低α\alphaα。
算法-数对的使用
2303_80050865的博客
05-19 190
【代码】算法-数对的使用。
高被引二区优化算法——肝癌算法（Liver Cancer Algorithm，LCA）深度解析+性能测试
woaipythonmeme的博客
05-19 778
LCA的核心机制聚焦于肿瘤在寻找最有利生存环境时所表现出的适应性与侵袭性行为，算法通过演化搜索策略再现肝癌细胞在器官中逐步扩张并主导空间的动态机制，其数学建模确保了算法在解空间内的全局探索能力与局部开采能力之间的高效平衡。为确定肿瘤的体积，我们采用一种基于数学模型的计算方法，假设肿瘤呈半椭球形，该形态已在包括肝癌在内的多种癌症中被观察到。在LCA算法的该阶段中，其设计灵感源自真实肿瘤的扩散过程，假设肿瘤可在竞争环境中逐步选择最优路径深入肝脏的不同区域以实现侵占。）时，目标代理元素的肿瘤位置将被考虑。
代码随想录算法训练营第60期第三十九天打卡
2401_83782806的博客
05-17 833
首先我们就直接看到这一道题目，看看我们是否可以发现究竟在考查哪一个算法：我们来看一下题意，就是我们有一堆石头，我们每一次可以选出任意两块石头并将其一起粉碎，如果两块石头的重量相同那么两块石头都会被完全粉碎，如果一块石头重量大一块石头重量小的话，那么我们重量小的石头会被完全粉碎，大的石头剩下的重量是大的石头减去小的石头，最后我们只会剩下一块石头，那么题目要求我们返回此石头的最小的可能重量，如果没有剩余就返回0，那么我们应该如何思考这一道题目呢？
算法练习：19.JZ29 顺时针打印矩阵
qq_34348690的博客
05-16 393
【代码】算法练习：19.JZ29 顺时针打印矩阵。
评论
添加红包

请填写红包祝福语或标题

个

红包个数最小为10个

元

红包金额最低5元

当前余额3.43元 前往充值 >
需支付：10.00元
成就一亿技术人!
领取后你会自动成为博主和红包主的粉丝 规则
hope_wisdom
发出的红包
实付元
使用余额支付
点击重新获取
扫码支付
钱包余额 0

抵扣说明：

1.余额是钱包充值的虚拟货币，按照1:1的比例进行支付金额的抵扣。
2.余额无法直接购买下载，可以购买VIP、付费专栏及课程。

余额充值